熱輻射計算を行うにあたり、OpenFoamの計算能力を確認しておこうと思います。
「目的」
OpenFoamの熱伝導解析ソルバーchtMultiRegionFoamの輻射計算機能の計算結果を検算する
「方針」
半球の発熱体を固体で囲んだ輻射状況を机上で理論計算を実施し、OpenFoam計算結果と比較する。

1.1 モデル設定
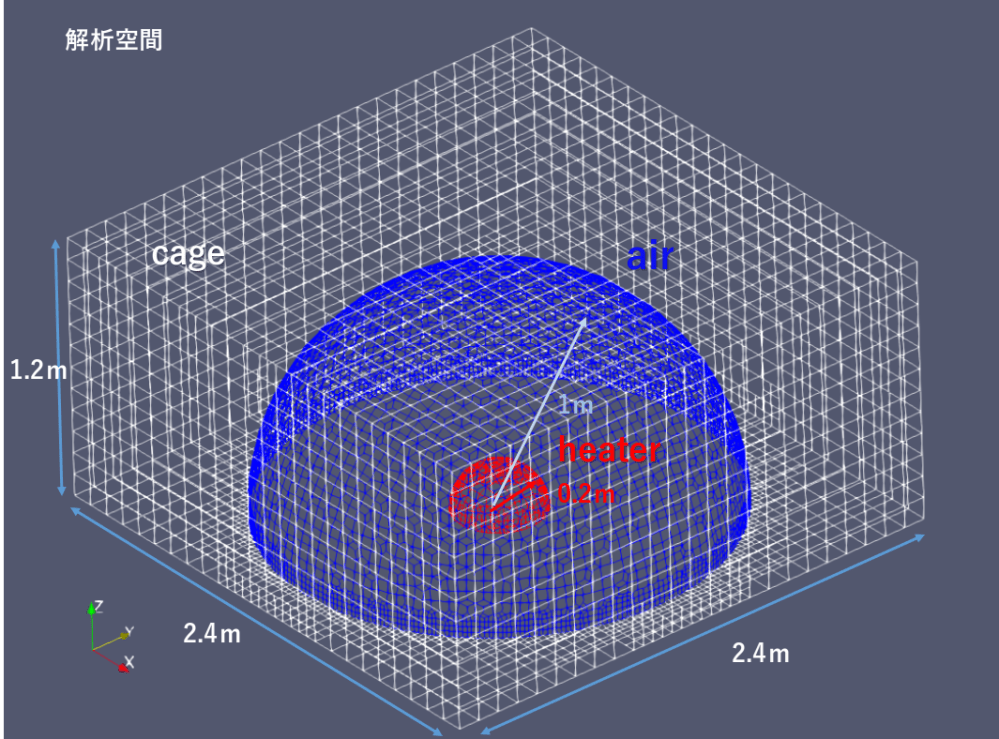
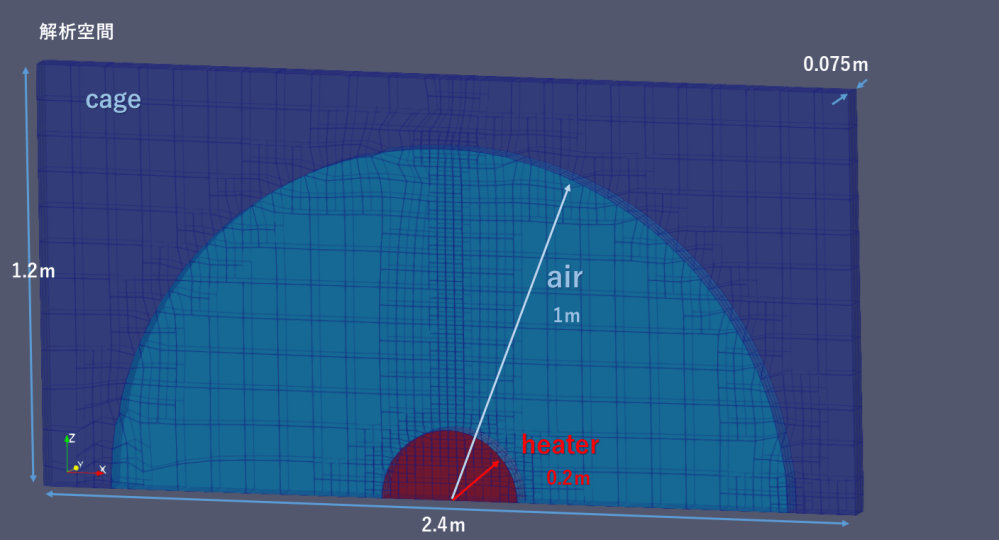
解析空間
・メッシュ:2.4(長さ)x2.4(幅)x 1.2(高さ)mを24x24x12の合計6912マスに分割。
・半円まわりのメッシュ粗さはrefinementSurfaces level(1 2)に設定(基本メッシュの21~22に分割)。
(レイノルズ数より想定される理想のメッシュサイズは1mm以下ですがPCメモリー制約のため最小25mm四方としました。)
結果、出来上がったメッシュが以下の図となります。
1.2 OpenFoam設定
Openfoamの設定を以下に示します。
[物性定義]
・heater(鉄):半径20cmの半円を中心に設置
熱伝導率:80[W/m/K] 比熱:450[J/kg/K] 密度:8000[kg/m3] モル重量:56[g/mol]
放射率、吸収率:1(計算容易化のため黒体とした:constant/radiationPropertiesファイル内)
(但し時短のため密度を1/10の800[kg/m3]に修正。これにより計算時間は1/10)
・air(空気層):heaterの周りを厚み80cmの空気層を設置
比熱:1000[W/m/K] 粘性係数:1.8e-5[Pa・s] プラントル数:0.7 モル重量:28.9[g/mol]
放射率、吸収率:viewFactorモデル※1使用のため設定なし
但し気体底面(minZ)は輻射計算に反映させないために、放射率1e-6、吸収率1とした。
(constant/boundaryRadiationPropertiesファイル内。0/G、0/IDefault及び0/qrファイル内も一応変更)
・cage(鉄):空気層の周りに半径1mの囲いを設置
パラメータ設定はheaterと共通とした。
[環境値定義]
・初期温度はすべて300[K](約30℃)に設定
・heaterの底面に定常250[W]を印加、cageの外面はすべて300[K](約30℃)で固定、airの底面はzerogradientで定義
・初速:全域上方0.01[m/s]に設定(境界面はすべて「0」で固定)
・初期圧力:全域1e+5[Pa]に設定。
[ソルバー定義]
・解析ソルバーはchtMultiRegionFoam(pimpleアルゴリズム)
(チュートリアルはchtMultiRegionSimpleFoam(定常解析用)ですが、当事業所でソースコードを理解することなくchtMultiRegionFoam(非定常解析用)に切り替えました)
・乱流モデルはRASに変更(chtMultiRegionFoamデフォルトはlaminar)
・乱流エネルギーk、乱流散逸率epsilonの初期値は[k=1e-6、epsilon=2.4e-9]と設定(設定根拠はこちらを参照方)。
・積分幅:0.02sec&自動調整。流速1[m/s]の時クーラン数は0.8
上記以外のパラメータは以下のOpenFoamチュートリアルの物をそのまま使用。
tutorials\heatTransfer\chtMultiRegionSimpleFoam\multiRegionHeaterRadiation
※1 viewFactorモデル:固体間2対の面を想定し、その面間の熱輻射形態係数を計算しているそうです。その際、気体内部の吸収、放射は考慮しないそうです。
[補足]
輻射計算特有の初期ファイル変更点を示しておきます。
・気体の初期条件フォルダにGファイル、IDefaultファイル、qrファイルを追加
・気体のfvSchemesファイルに「div(Ji,Ii_h) Gauss linearUpwind grad(U)」追加
・気体のfvSolutionファイル中、「 “(U|h|k|epsilon|R)”」を「”(U|h|k|epsilon|G|Ii)”」に変更
・気体のfvSolutionファイルにrelaxationFactors欄追加(変数1の場合、実質影響なし)
・気体のboundaryファイル内の全ての面定義を「inGroups 2 ( wall viewFactorWall )」に変更
(輻射に関与しない面も変更必要。ここでは気体領域のminZ。ここを1(wall)のままにすると輻射計算qrの全体収支が全く合わなくなる(viewfactorモデルの制限と推定されます。)
・気体のconstant/air/boundaryRadiationPropertiesファイル内の底面minZの放射率を「1e-6」に変更(変更しなかった場合の計算結果を後述「追記1」に示します。
・「chtMultiRegionFoam」実行前に以下のコマンド実施
・「faceAgglomerate -region air」により初期条件フォルダにfacesAgglomerationを生成。
尚constant/air/viewFactorsDict内に「writeFacesAgglomeration true;」を追加しないと起動しません。
但しこのコマンドを実施しなくても計算結果は変わりませんでした。
・「viewFactorsGen -region air」により初期条件フォルダにviewFactorを生成。
1.3 計算結果
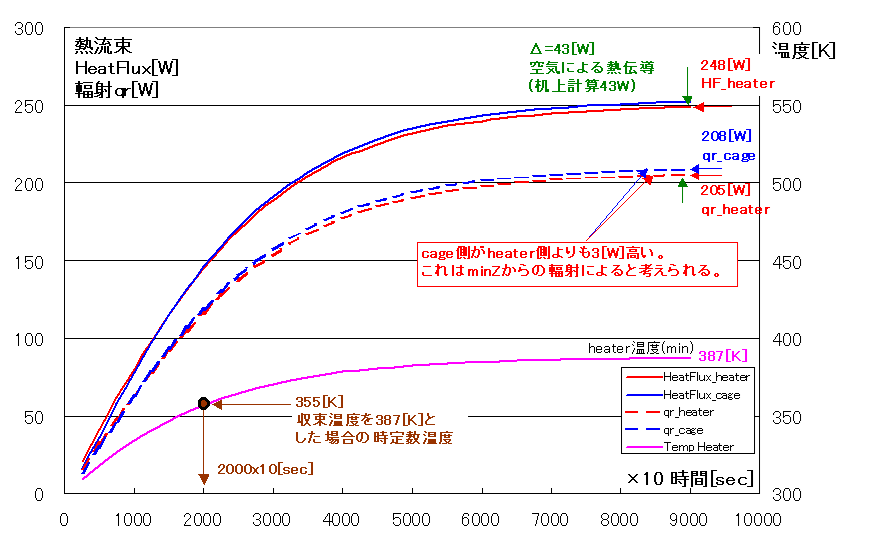
9000×10秒(25時間)後の計算結果を示します(対応する理論計算は1.4項に示します)。

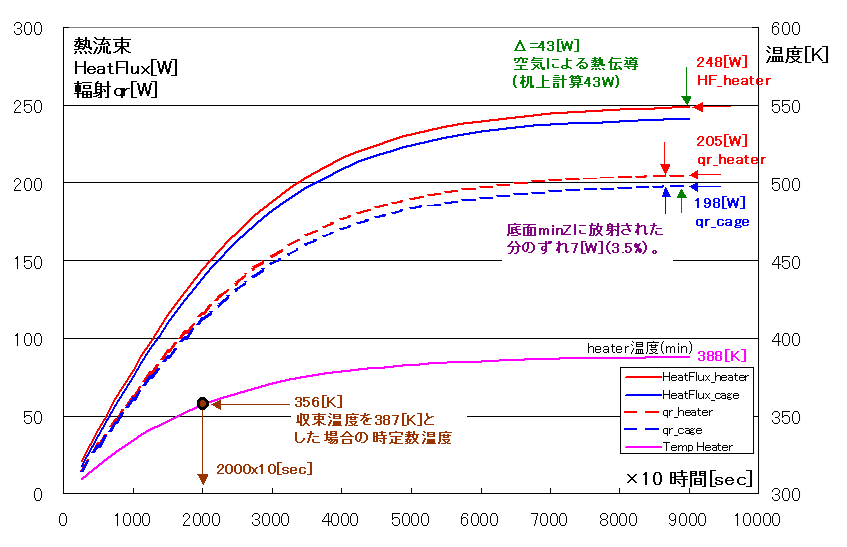
・heaterから放出される総熱量wallHeatFluxは248[W]と入力熱源250[W]に収束していく。
・空気による熱伝導はOpenFoam計算値qr205[W]とwallHeatFlux248[W]の差分より43[W](理論計算43[W]:次項)
・温度は400[K]に近い388[K]に収束し、収束時定数はグラフより凡そ20000sec(単純計算24000sec:次項)。
・流速は最大0.35[m/s]程度でRASモデルを使う必要はなかったようです。
以上よりOpenFoamのchtMultiRegionFoamの計算結果は理論計算(1.4項)と十分一致しているようです。
尚cage輻射量qrが197[W]でheater輻射量qr205[W]よりも収束近傍で7[W](4%)少なくなっています。
この点を少し詳しく検討した結果を1.5項に示します。
1.4 理論計算
(1)heater温度
ステファン・ボルツマンの法則より発熱体の輻射エネルギーE[W/m2]は以下の式で示すことが出来ます(参考文献[1]4.4章)。
E = ε1×ε2×Sa×σ(Ta4-Tc4)
ε1:放射率(今回は1とした)
ε2:形状係数 発熱体の微小面が相手側の面に視認出来る割合。今回のモデルでは「1」と考えられる。
Sa:発熱部面積 2πr2=0.251[m2]
σ :ステファン・ボルツマン定数 5.67e-8[W/m2/K4]
Ta :発熱体温度[K]
Tc :cage温度300[K]
今回のモデルでは上記輻射エネルギーEがheater発熱量250[W]に収束すると考えられる。
E=250[W]=ε1×ε2×Sa×σ(Ta4-Tc4)
よってTa=400[K](130[℃])
よって空気層の伝熱が無視出来る場合はheaterは400[K](130℃)まで昇温すると考えられます。
(2)収束時間
印加熱量250[W]で100K昇温する時間は放熱がないとすると
ρCpVΔT/E=8000[kg/m3]*450[J/kg/K]*4π(0.2)3/3[m3]/2*100[K]/250[W]=24127[sec]
1次遅れの場合、時定数はこの値よりも小さくなりますが、ここでは規模を見る意味でこの値を使います。
(3)伝熱
空気の伝熱を考えてみます。熱伝達率Hは以下の式で推算します。
水平流体層における自然対流の熱伝達率h計算(参考文書[1]3.7.4項)
h= 0.069×k×{gβ(Tw-Te)/(αν)}1/3×Pr0.074=3.38[W/m2/K]
k:熱伝導率 空気 0.0286[W/m/K]
g:重力定数 9.807[m2/s]
β:体積膨張係数 1/Te[K]
Tw:発熱体表面温度 400[K]
Te:周囲温度 300[K]
α:熱拡散率 空気 3e-5[m2/s]
ν:動粘度 空気 2e-5[m2/s]
Pr:プラントル数 空気 0.7
上式hの使用条件:105<Ra<109
Ra:レイリー数{gβ(Tw-Te)L3/(αν)}=3e9 (若干オーバー)
L:気体厚み 今回は0.8m
qr = h×S×ΔT=43[W]
S:発熱体断面積 0.126[m2](上昇気流のため表面積ではなく断面積とした)
ΔT:温度差 100[K]
以上より空気による熱伝導は43[W]という計算になりました。
1.5 輻射漏れ
cage輻射量qrが197[W]でheater輻射量qr205[W]よりも収束近傍で7[W](4%)少ない計算結果でした。
これはheaterとcageの隙間から輻射が自由空間に漏れていくためです。漏れの様子を覗き込む角度を変えて見てみます(真横より角度11.5°、40°、70°から覗き込んだ場合の視野)。


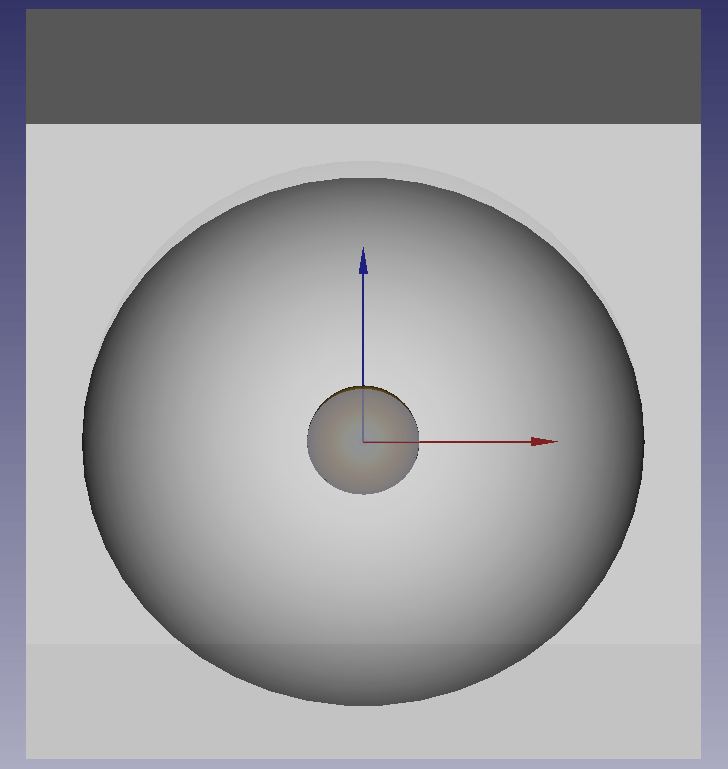
これは以下の式で定義されるviewFactor(形状係数)によるものとなりますが、今回のケースを机上計算することは難しいと考え、簡単な概算を試みます。
F12 = 1/A1×∫A1∫A2(cosθ1cosθ2/πr2)dA1dA2 (参考文献[1]4.4.3項)
F12:面1から見た面2の形状係数
A1、A2:面1、面2の面積
θ1:面1の微小面積dA1から面2の微小面積dA2を見た場合の角度(法線方向からのずれ)
θ2:θ1と同様。
・概算
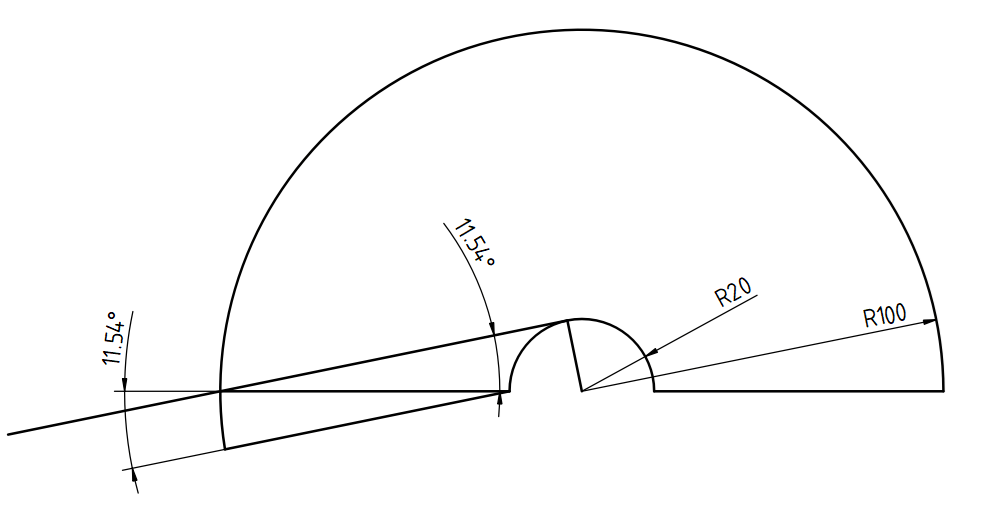
上図で分かる通り、角度が増えていくとheaterの発熱面が見えなくなっていきます。更に輻射はその見る角度θに対しcosθの比で減衰していきます。このためここでは輻射漏れを11.5°の時のみ考えることとします。
すると下図のごとく、視野は11.5°となり本来の放射面180°に対し、凡そ11.5/180の輻射エネルギーが放出されることが仮定出来ます。
更に視野に入ってくる輻射面は視野に対し直角ではありません。ここではえいやで45°としておきます。
結果漏れ量は11.5/180×cos45=4.5%という概算結果となり、FreeCADの計算結果4%とほぼ一致します。
「追記1」
1.2項OpenFoam設定にて示しました通り気体底面(minZ)を以下の特殊な設定としました。
・emissivity(放射率) 1e-6;
・absorptivity(吸収率) 1.0;
これは気体底面を輻射計算に含めないためでしたが、ここでは通常の以下の設定(黒体)で計算して見たいと思います。
・emissivity(放射率) 1.0;
・absorptivity(吸収率) 1.0;
計算結果は以下となりました。
・内側(heater)の輻射熱qr205[W]に対し外側(cage)の輻射熱qrが208[W]と3[W]も大きくなっている。
・気体による熱伝導量43[W]及び時定数20000secはほぼ変化なし。
この輻射熱の挙動は気体底面(minZ)からの輻射によるものと考えられます。
paraViewの積分関数を用いて気体底面minZの放出輻射量を求めた結果が10.4[W]でした。
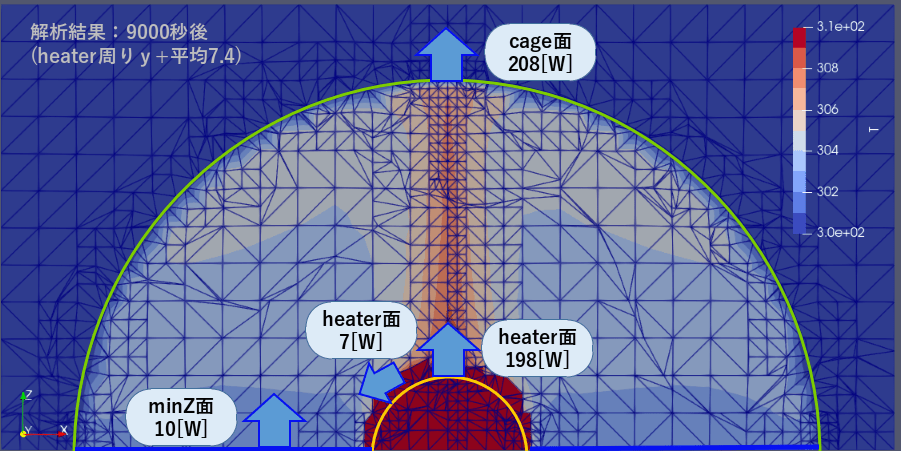
1.4項計算結果よりheaterから放射された輻射熱205[W]の内、198[W]がcage側に向かい、残り7[W]は気体底面minZに吸収されたと考えられます。ここで気体によって熱せられた境界面minZより3[W]が足され計10[W]がcage側に放出され他と考えます(heater側にも若干は放出)。結果cage側の吸収する輻射熱が208[W]となったと考えます。
「所感」 輻射熱計算においては輻射qrの面間の収支確認することが重要と感じました。
「追記2」
計算時間短縮のため固体密度を1/10にして計算していますが、ここでは更なる時短を試みます。
heater及びcageの密度を1/100にした場合の計算結果を下記に示します。
結果、以下の違いが出ました。
・Heaterとcageの熱流束HeatFluxが一部乖離。
この原因として固体側が時短のため、100倍早く熱伝導が進行していくのに対し、気体側が追いつていけないためと考えられます。
一方以下はおおよそ変化していません。
・Heaterとcageの輻射qrはずれを含め1/10時短とほぼ同じ動き。
・Heater側熱流束HeatFlux及び輻射qrだけを1/10時短と比較するとほぼ同じ。
・このため空気による熱伝導も1/10時短とほぼ同じ44[W]。
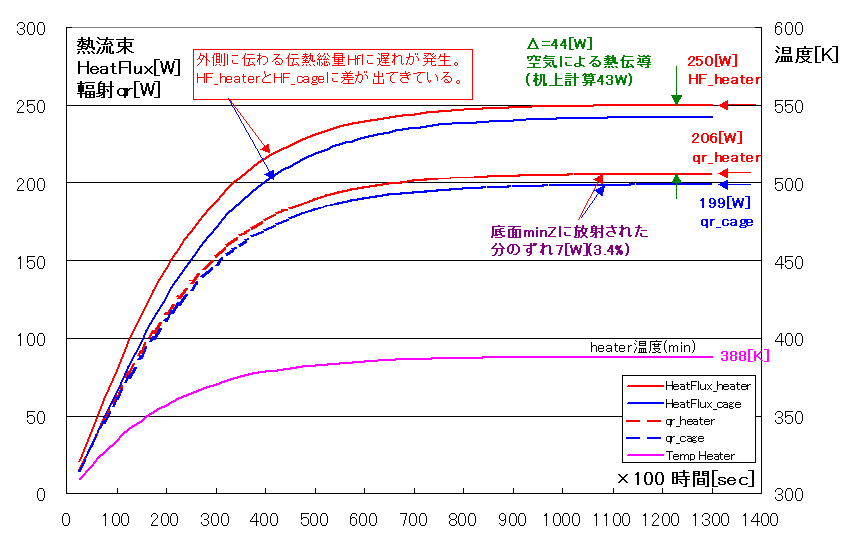
1/100時短を行っても概ね一致していますが、それでも今回のような計算(温められた気体が更に別の個体を温める計算)での時短は1/10程度が限度と考えます。
「追記3」
メッシュが細かくなっていくとviewFactors作成時のメモリ不足が発生します。その解決のため2D解析にトライしてみます。ところがviewFactorGenが2D計算では動きませんでした。ネット情報ではコード修正が必要なようです。
そこでコード修正までは手を出さず、以下の方法で近似的に2D計算を模擬しようと考えます。
・25mm厚を3層(径75mm)の薄板に設定。
・薄板面の境界条件をzeroGradientに修正(p、p_rgh、T、Uのみ。他項目は他の面と同じまま)
(通常2D模擬ではsymmetryPlaneを使うがviewFactorモデルではエラー発生)
・側面及び底面を3Dと同じ輻射特性の放射しない(放射率1e-6)、吸収のみ(吸収率1)とした。
・時短のためheater及びcageの密度を1/10の800[kg/m3]に修正。
[OpenFoam設定補足]
疑似2D化の際のOpenFoam変更点を示しておきます。
・薄板面の境界条件をzeroGradientに修正(p、p_rgh、T、Uのみ。他項目は他の面と同じまま)
・メッシュ作成手順を以下の順番に変更
「blockMesh」⇒「surfaceFeatureExtract」⇒「snappyHexMesh」
⇒「extrudeMesh」⇒「splitMeshRegions 」
計算結果を以下に示します。

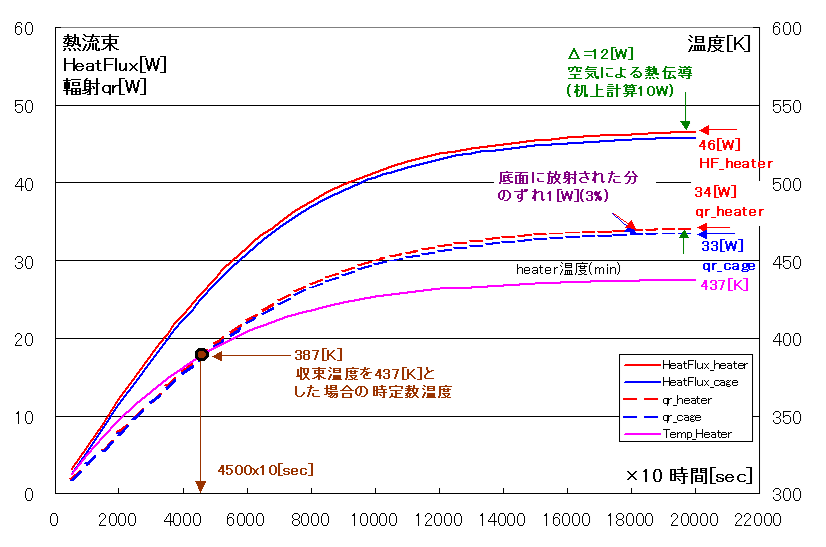
・空気による熱伝熱はOpenFoam計算値qr34[W]とwallHeatFlux46[W]の差分より12[W](理論計算10[W]※2)
・温度は400[K]を僅かに超えて437[K]に収束し、収束時定数はグラフより凡そ45000sec(単純計算36000sec※2)。
・heater輻射量34[W]とcage輻射量33[W]は僅かなずれとなっている。
以上輻射量qrと熱量wallHeatFluxは3D計算と様相がよく一致しているのですが、heater温度が異常に高くなっています(予定400[K]が437[K])。輻射量は4乗に比例しますので(4004-3004)/(4374-3004)=62%の輻射面積減少に対応します(正確には立体角が減少)。
当事業所にていろいろなパータンで試してみた結果、上述収束温度異常の原因として以下を推定しています。
・viewFactorモデルの形状計算では放射率=吸収率とし、吸収率の設定は考慮されない。
・viewFactorモデルでは面同士が垂直の場合、数値計算上、例え立体角が有限でも形状係数が「0」になってしまう。
上述薄板モデルではheater面と側面が垂直同士のため、相当な面の形状係数が「0」となってしまい、輻射面積が減少したと推定しました。
そこで以下のようにモデルを修正しました。
・25mm厚を3層(径75mm) ⇒ 25mm厚を9層(径225mm)
計算結果を以下に示します(熱源を3倍にし、計算結果は1/3に補正しています)。


・空気による熱伝熱はOpenFoam計算値qr37[W]とwallHeatFlux47[W]の差分より10[W](理論計算10[W]※2)
・温度は410[K]に収束し、収束時定数はグラフより凡そ35000sec(単純計算36000sec※2)。
・heater輻射量37[W]とcage輻射量36[W]は僅かなずれとなっている。
以上より温度は410[K]とかなり400[K]に近づきました。更に厚みを増せば更に温度が下がると思われますが、既に厚みが225mmであり、これ以上は2D模擬とは言い難い状況になっています。計算時間と相談しながら厚みを決めることになりそうです(9層の計算で3時間20分かかっています)。
「所感」
viewFactorモデルの癖として以下を痛感しました
・立体角が有限だとしても壁面の形状係数は「0」になっていると思われます。
・形状係数の一部が「0」となると輻射相手面が減少 ⇒ 輻射熱総量の減少
※2:[机上理論計算]
(1)輻射熱量
E = ε1×ε2×Sa×σ(Ta4-Tc4)=46.8[W]
ε1:放射率(今回は1とした)
ε2:形状係数 発熱体の微小面が相手側の面に視認出来る割合。今回は「1」と考えられる。
Sa:発熱部面積 πrd=0.2*.075π[m2]
σ :ステファン・ボルツマン定数 5.67e-8[W/m2/K4]
Ta :発熱体温度400[K]
Tc :cage温度300[K]
(2)収束時間
印加熱量46.8[W](輻射熱量と同じとする)で100K昇温する時間は放熱がないとすると
ρCpVΔT/E=8000[kg/m3]*450[J/kg/K]*π(0.2)2*0.075[m3]/2*100[K]/46.8[W]≒36000[sec]
(3)伝熱
h= 0.069×k×{gβ(Tw-Te)/(αν)}1/3×Pr0.074=3.38[W/m2/K]
k:熱伝導率 空気 0.0286[W/m/K]
g:重力定数 9.807[m2/s]
β:体積膨張係数 1/Te[K]
Tw:発熱体表面温度 400[K]
Te:周囲温度 300[K]
α:熱拡散率 空気 3e-5[m2/s]
ν:動粘度 空気 2e-5[m2/s]
Pr:プラントル数 空気 0.7
上式hの使用条件:105<Ra<109
Ra:レイリー数{gβ(Tw-Te)L3/(αν)}=3e9 (若干オーバー)
L:気体厚み 今回は0.8m
qr = h×S×ΔT=10[W]
S:発熱体断面積 0.4*0.075[m2](上昇気流のため表面積ではなく断面積とした)
ΔT:温度差 100[K]
「追記4」
上項にて輻射の様子を詳しく見てきましたが、ここでは空気による熱伝導の様子を机上計算で確認しておきます。流体計算の検証のため、幾分CFD計算結果ありきの計算ではありますが、一応オーダー確認を試みてみます。
〇流速0.35[m/s]
1.3項の計算結果より90000秒経過後の空気の上昇気流速度は0.35[m/s]に達しています。この数字を当事業所オリジナルの概算で確認してみます。
上昇気流速度が一定の段階では以下の力が等しくなっていると考えられます。
・温度上昇による浮力
・粘性力
それぞれを数式で表現してみます。
[浮力Flift]
Flift = ρgS0h(Tm-Te)/Te = 0.0113[N]
ρ:空気密度1.225[kg/m3]を使用
g :重量定数9.807[m/s2]
S0 :上昇気流断面積 πr2=π*0.152=0.0707[m2](r=0.15は1.3項CFD計算結果より)
h :上昇気流高さ0.8[m]
Tm:上昇気流代表温度 これも1.3項CFD計算結果より305[K]
Te:周囲温度 300[K]
[摩擦力Ffliction]
Ffliction = μS1u/d[N]
μ:空気の粘性係数 1.8e-5[Pa・s]を使用
u:求めるべき上昇気流速度[m/s]
d:uの速度勾配を代表する寸法 ここではBlasiusの式※3よりd=2*√ν/√u
ν:空気の動粘度 1.5e-5[m2/s]を使用
S1:上昇気流の全行程の濡れ面積 下図より6.3π[m2]
Flift = Ffliction よりu=0.39[m/s]
OpenFoamの計算結果は1.3項より最大0.35[m/s]、全域0.1[m/s]で概略推算値0.39[m/s]はオーダーとして一致していると考えます。
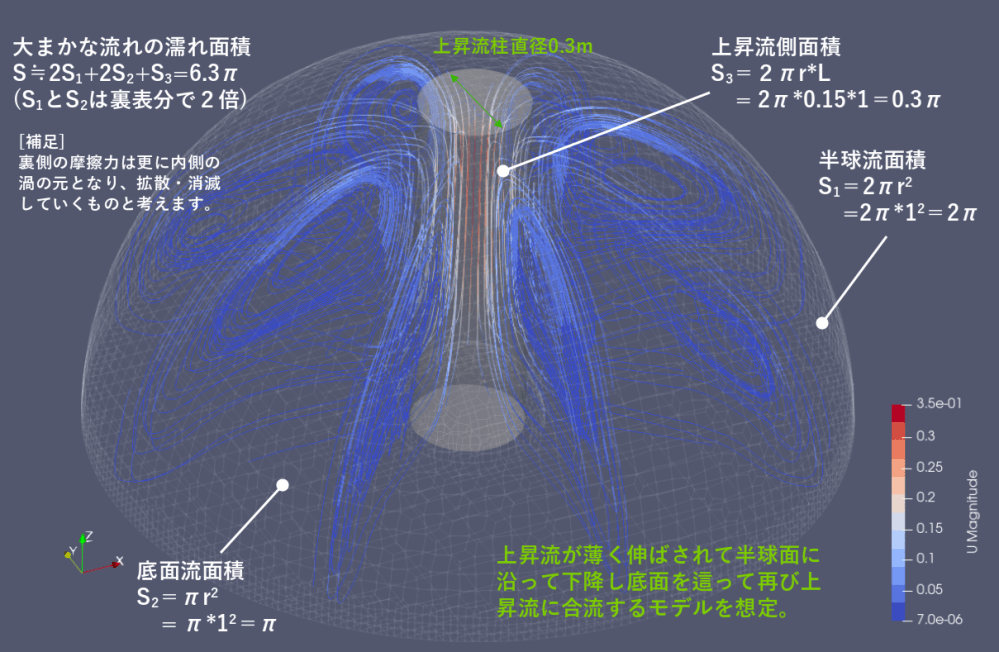
※3:Blasiusの解:層流境界層厚さを示す式(関連文章[1]3.4.1項)
d = η*x/√Rex = η*x*√ν/√(u*x) = 2*√ν/√u
η:速度分布比(u/ue) 境界層という意味ではη=5となるが、u/ue≒60%という観点でη=2とした(適当)。
x :代表長さ。ここではcage半径1[m]を採用。
〇昇温温度 5[K]について
1.3項の計算結果より90000秒経過後の空気の上昇気流速度0.1[m/s]の分布に対応する温度上昇が5[K]になっています。この数字を当事業所オリジナルの概算で確認してみます。
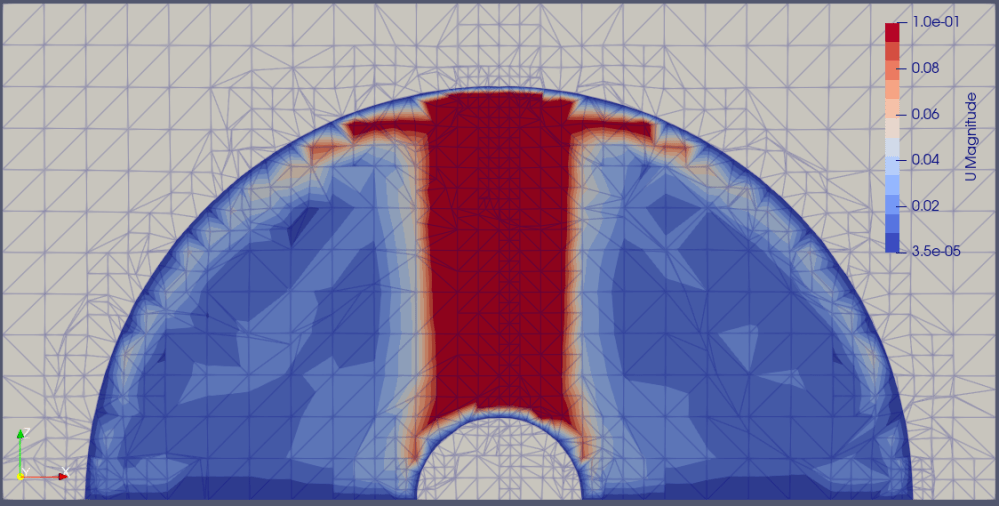

概算するにあたり以下の簡略モデルを想定しました。
・上昇流は頂上に達した後、半球面を下り底面を這う。その後heater表面にそって昇り、上昇流と合流する。
・heater表面に沿って上昇する間にheaterから加熱される。この際、境界層を表現するためにこの流れを2層に分ける
(境界層+第2層)。
・上昇流速度及びheater周り速度は1.3項の結果から0.1[m/s]と設定。
以上の想定を図示します。

この概算を以下のステップで計算していきます。
step1:境界層及び第2層の厚みの検算
step2:境界層及び第2層の温度上昇値検算
step3:境界層及び第2層の混ざりこみによる温度検算
・step1:境界層及び第2層の厚みの検算
境界層の厚さδ1は前述Blasiusの解を用い、η=2(u/ue≒60%)とした結果δ1=11[mm]となりました(下式:η=2は適当)。
δ1=η*x/√Rex=η*x/√(u*x/ν)=11[mm] @η=2、x=0.2[m]、u=0.1[m/s]
また上図境界層の速度はu/ue≒60%より最大0.1×0.6[m/s]となりますが、代表値として半分の0.03[m/s]としました。
第2層の厚みは質量保存(下式)より77mmと計算しました。
上昇気流体積V0(単位時間当たり)
V0=πr2×u=π×0.22×0.1=0.004π[m3/s]
境界層体積V1(単位時間当たり)
V1=π((r+δ1)2-r2)×0.3u=π×(0.2112-0.22)×0.03=π*1.36e-4[m3/s]
第2層体積V2(単位時間当たり)
V2=π((r+δ1+δ2)2-(r+δ1)2)×u=0.1(0.211+δ2)2π-0.00445π[m3/s]
V0=V1+V2よりδ2=77[mm]
第2層の速度は0.1[m/s]となります。
・step2:境界層及び第2層の温度上昇値検算
一辺の温度を固定した場合の1次の熱伝導方程式は以下となります。
∂T/δt = αδ2T/δx2
α=k/(ρC)
k:熱伝導率 空気 0.0286[W/m/K]
ρ:密度 空気 1.225[kg/m3]を使用
C:定圧比熱 空気1000[J/(kg・K)]
この方程式の解析解は以下となります(関連文章[1]2.3.3項)。
ΔT=(Th-Te)[1-erf(x/(2√(αt)))]
erf(ξ)=2/√π・∫e-y2dy|y=0~ξ:誤差関数(エクセルの関数に含まれています)
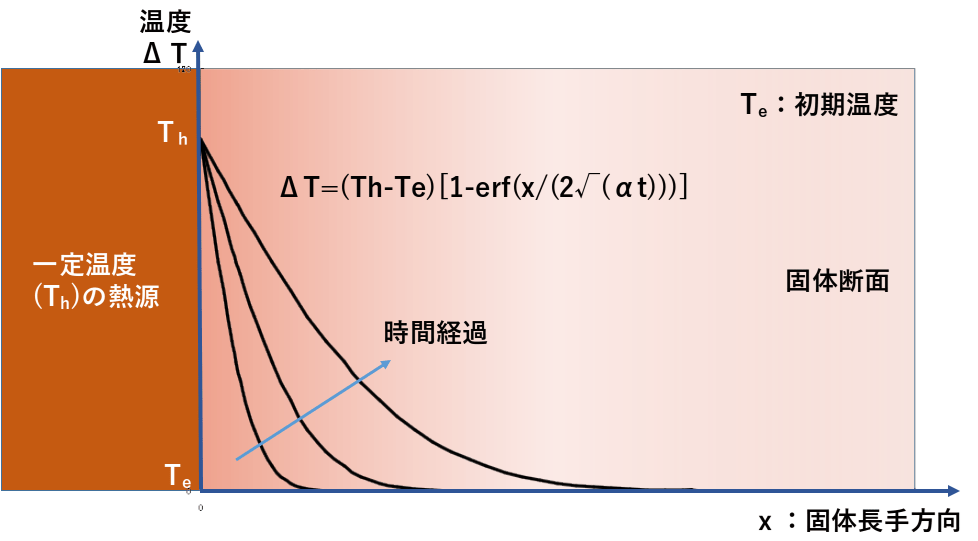
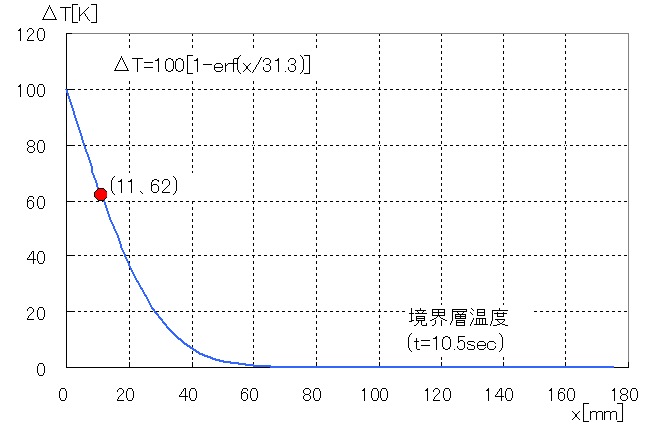
この式を境界層に当てはめてみます。
Te:初期温度300[K]
Th:ヒーター温度400[K]
t:ヒーター回り込み時間 πr/2÷0.3u=10.5[s]
2/√αt=31.3[mm]
エクセル計算より境界層の縁δ=11[mm]での温度ΔTは62[K]となります。
境界層全体の代表温度は0[K]と60[K]の中間で31[K]とします。
(境界層と第2層の境界面では最初0[K]が10.5秒後には62[K]に到達するという状況です)
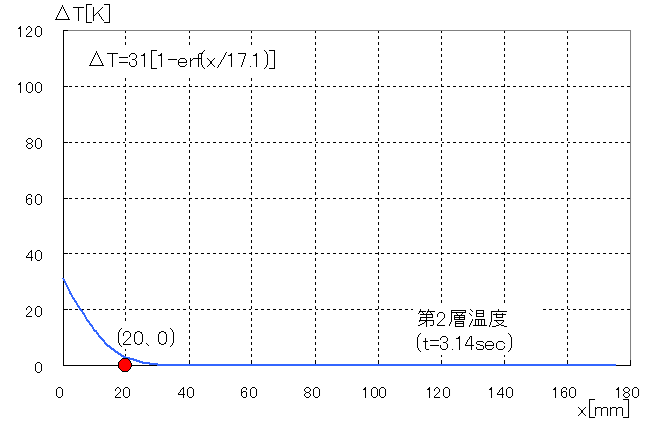
続いて第2層に当てはめてみます。
Te:初期温度300[K]
Th:境界層縁温度331[K]
t:境界層回り込み時間 πr/2÷u=3.14[s]
2/√αt=17.1[mm]
エクセル計算より第2層の縁δ=77mm(下図)での温度ΔTは0[K]となります。
第2層ではδ=20mm程度まで昇温され、それ以上離れた場所は0[K]のままとなることが見て取れます。
第2層のδ=20mmまでの代表温度は0[K]と31[K]の中間で16[K]とします。
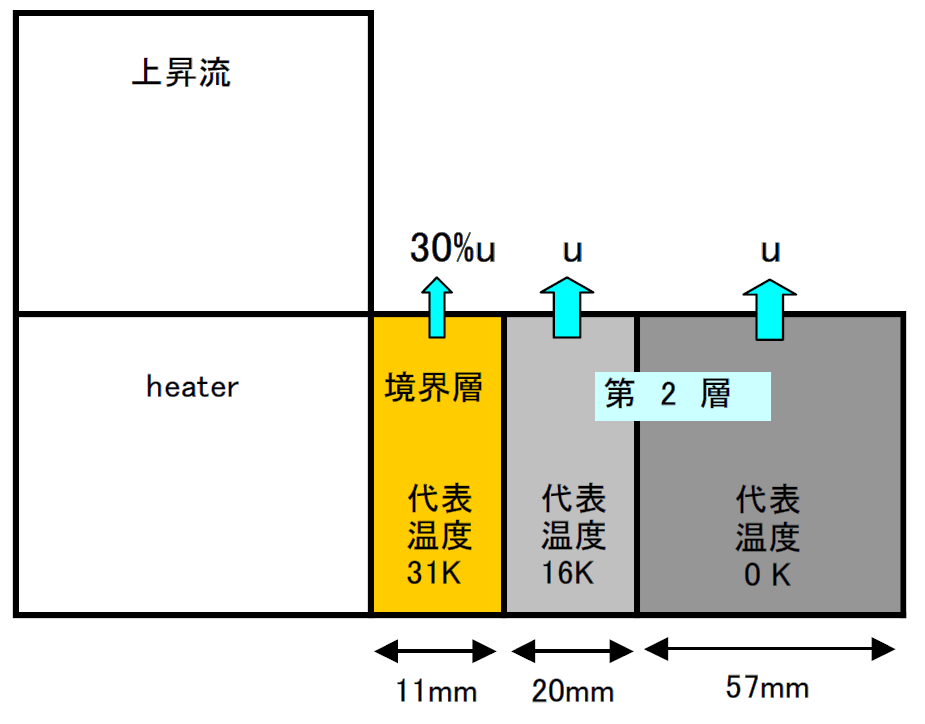
・step3:境界層及び第2層の混ざりこみによる温度検算
step1およびstep2をまとめると下図のような結果となりました。
この層が混ざり合うことにより得られる温度は以下の式から計算され、結果5.3[K]の昇温となります。この結果は1.3項のOpenFoamの計算結果5[K]とよく一致しています。
{31[K]×11[mm]×30%(境界層分)+16[K]×20[mm](第2層の一部)} ÷ {11[mm]×30%+20[mm]+57[mm]} = 5.3[K]
(円周方向の面積変化は無視)
「所感」
かなりな労力をかけてなんとか手計算でOpenFoamの計算値を確認しました。
検算は重要ですが、それにしてもOpenFoam実行の方が簡単です。
参考文献
[1]JSMEテキストシリーズ 伝熱工学 日本機械学会 丸善出版
