１．パラメータの種類

１．１　k 乱流運動エネルギー(turbulent kinetic energy)

　kは単位体積あたりの乱流の運動エネルギーで、流体粒子の平均速度からの変動成分の二乗平均として定義されます。

　　k=1/2*(u’*u’)

　　　u’​：平均速度からの変動成分（時間平均）

　このパラメータにより乱流のエネルギー的な強さは分かるのですが、渦のサイズは分かりません。

　設定値としては下記乱流強度(無次元)で一般的には1～10％程度(乱流の状況による)に設定するようです。

　　　ｋ=3/2*(UI)2

　　　Ｉ：乱流強度

　2.2項の計算結果を例に示します(乱流強度5％)。

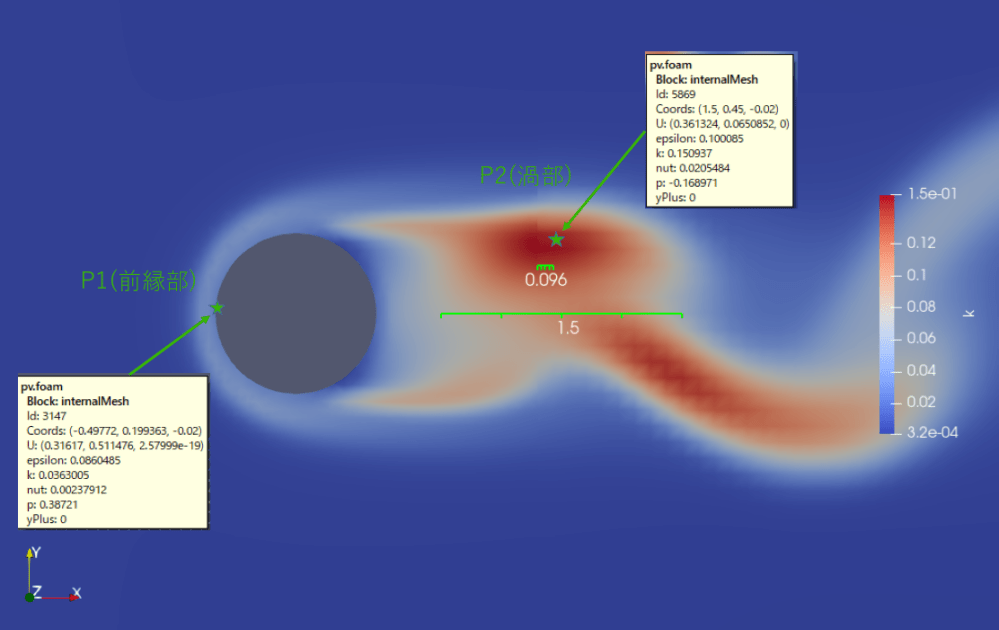
　計算初期値はk=0.00375でしたが、下図の最も大きいところではk=0.15に成長しています。

１．２　ε 乱流エネルギー散逸率(turbulent dissipation rate)

　乱流運動エネルギーkが粘性によって熱に変換される速さを表し、以下で定義されます。

　　　ε=(C_μ^3/4・k^3/2)/ℓ_m

　　　　C_μ：モデル定数=0.09(一般値)

　　　　ℓ_m：混合長=0.07L(一般値)

　　　　L：代表長さ

　εが大きいということはその地点の渦により活発に熱に変換されている様子を示しているそうです。

　計算初期値はε=0.00054でしたが、下図の最も大きいところではε=0.15に成長しています。

　kとεにより乱流モデルの状況が見えてきます。

　　・乱流内渦の寿命のオーダー：k/ε

　　・渦の大きさのオーダー(混合長)：(C_μ^3/4・k^3/2)/ε

	P1	P2
k/ε：寿命	0.42sec	1.5sec
ℓm：混合長	13mm	96mm

　例えばP2での渦の大体の大きさが96ｍｍ、その規模は速度1[m/s]×寿命1.5[sec]で1.5ｍとなり図示したような感じになり、渦の様子がイメージし易くなります。

[ε補足]

　εは乱流エネルギー輸送方程式(ナビエストークスの方程式を変動速度分ｋに焦点を当てたエネルギー収支式)にて以下の式で定義されます。

  ε= ν(∂u’_i/∂x_j)(∂u’_i/∂x_j)

　　　u’_i：時間平均からのi軸速度の変動成分（乱れ）

　　　下線（バー）は時間平均

　εは輸送方程式中[∂ｋ/∂t]と同次元であり、意味合いとしては乱流内部摩擦力によるエネルギー消滅の時間的割合を表していることになります(名前通り乱流エネルギー逸散率)。

　実務上は小さな渦が熱として消えていく領域を可視化していると考えて良いと思います。小さな渦の発生場所はｋで確認され、このεが大きいところほど短時間で消えていくことが判断できます。本文計算例ではεは小さな渦と流れの穏やかな領域との境界面に発達しています。

　尚内部摩擦力のもともとの定義は以下となります。

　　Ｆ=μ・du/dy=ρν・du/dy

　　　μ：粘性係数(OpenFoamではmuと表記)

　　　ν：動粘度(OpenFoamではnuと表記)

　　　ρ：密度

１．３　nut 乱流動粘度(turbulent viscosity：動粘度nuの乱流部分の意)

　乱流が周囲に運動量を拡散しているかを通常の粘性と同単位で示しており、渦が活発にかき乱している指標だそうです。εは乱流以外でも速度勾配の大きなところに発生しますが、nutは乱流のある場所(運動量交換が起きている場所)に発生します。

　以下の式で定義されます。

　　　nut=C_μk²/ε

　本パラメータはk-εモデルでは上式で計算されるそうなのですが、初期値「0」を設定する必要があります。初期設定ファイルを省略するとpisoFoam実行でエラーとなります。

[nut補足]

　以下の式においてｋの部位は乱流運動エネルギー、ｋ/εの部位は寿命を表現しています。

　　nut = C_μk²/ε

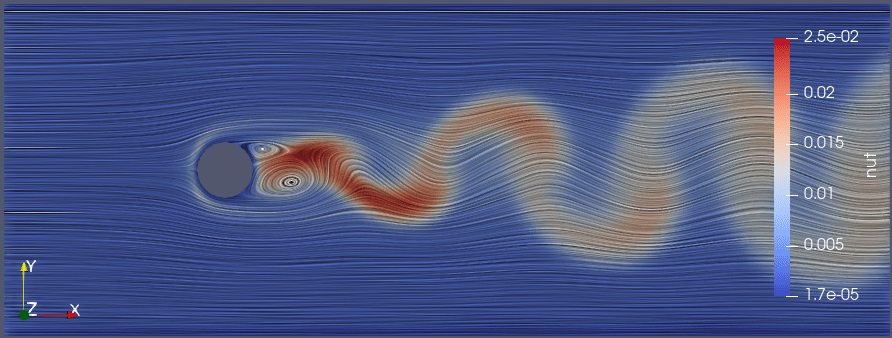
　実務上は小さな渦が消滅しないで下流に伝わっていく領域を可視化しています。

　(例えｋが小さくても、その渦の寿命が伸びることで下流に伝わっていく様子を示しています)

　尚paraviewにはsurfaceLIC(Line Integral Convolution)という表示方法があり、瞬間的な渦の様子が可視化されます。今までのパラメータを見直してみます。

　ｋ及びεは層流に近い領域でも赤く染まるのに対し、nutは乱流の領域で飲み赤く染まっていることが見て取れます。

〇k：乱流運動エネルギー

〇ε：乱流エネルギー散逸率

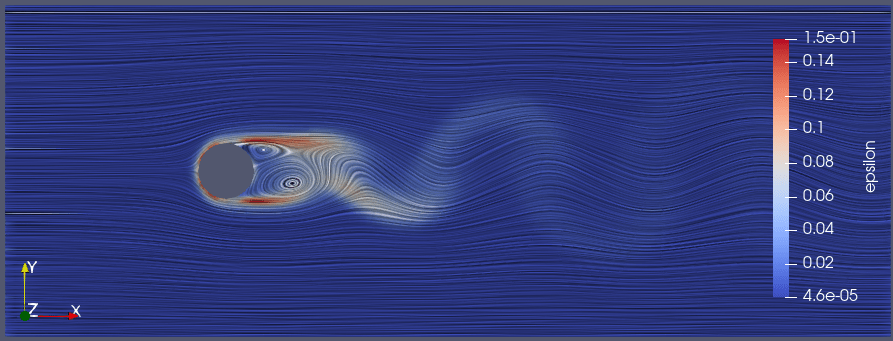
〇nut：乱流粘性係数

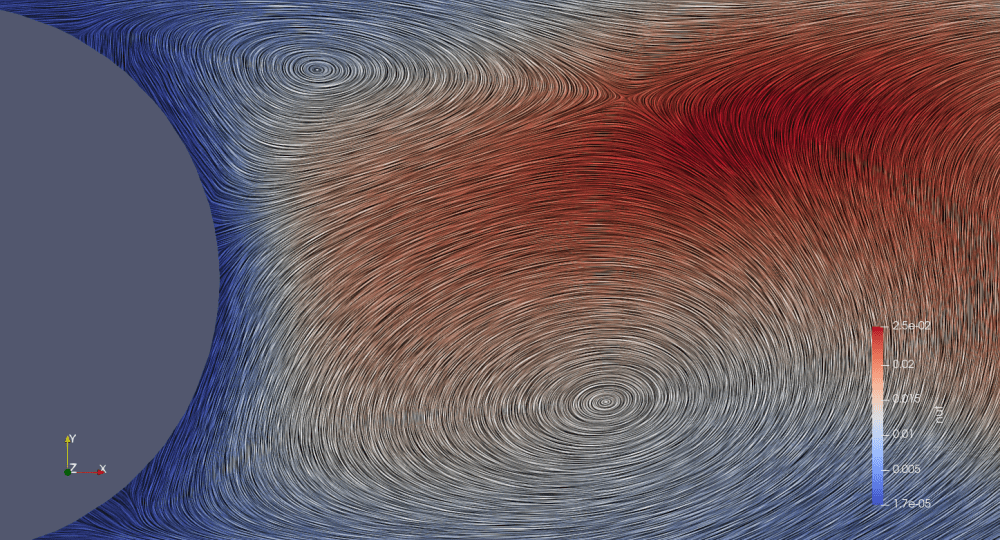
「注意」

　LICで可視化された渦はCFDで計算されたものを補間表現してるため、サイズは当てになりません。

具体的には上記計算結果のうち、円柱後方を拡大してみます。surfaceLICはメッシュサイズよりも小さい渦を表現していますが、それはCFDの直接の計算結果ではありません。

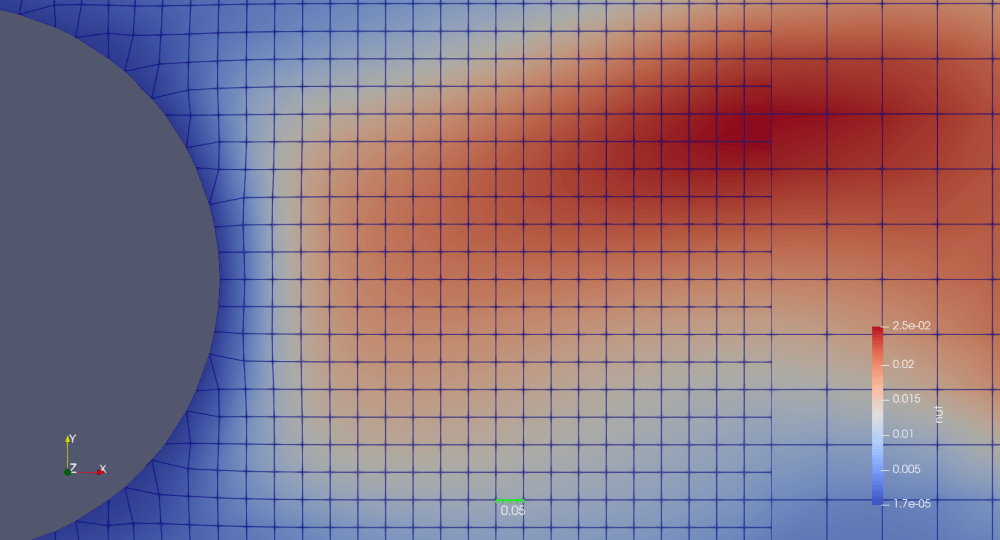
１．４　alphat 乱流熱拡散率(turbulent thermal diffusivity)

　乱流渦による熱拡散能力を示しており、渦が熱を拡散している指標だそうです。

　以下の式で定義されます。式から見てnutと同じ様相を示すことが分かります(下図：サーボ・モータ熱解析結果)。

      alphat=nut/Pr_t

    　Pr_t：乱流プラントル数=0.85(経験的)　本パラメータもk-εモデルでは上式で計算されるそうなのですが、初期値「0」を設定する必要があります。初期設定ファイルを省略するとchtMultiRegionFoam実行でエラーとなります。

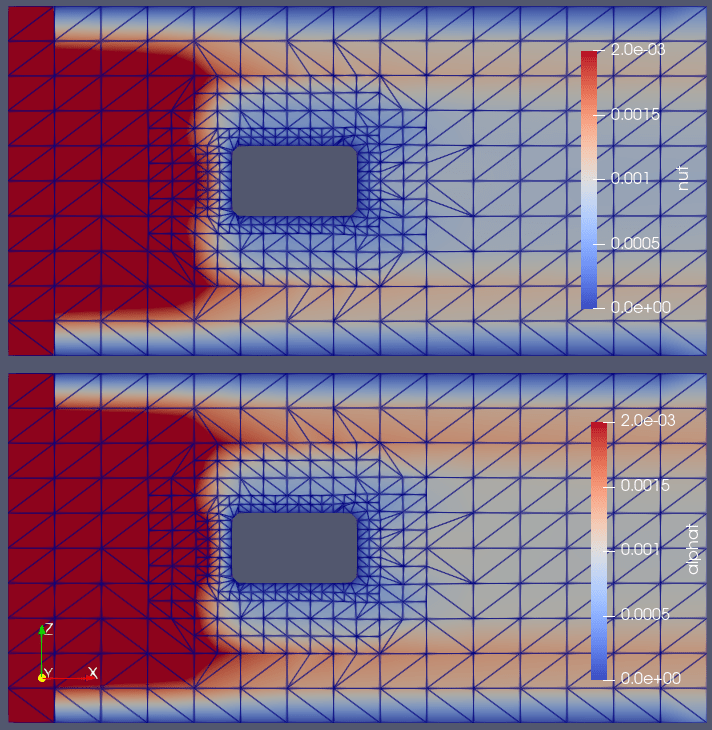
[alpht補足]

　乱流プラントル数の定義式が以下です。

      P_rt = nut / alphat ≒ 0.85(経験値)

　この式の意味するところはnutとalphatは同次元(nut[m²/s]、alphat[kg/m/s]で密度分の違い)ということで、実際alphatの意味は温度変化を解く方程式における減衰項(温度勾配を無くす力)の役割を持っています(nutはナビエストークス方程式における減衰項)。　そしてこの0.85の意味合いは「物体の後流に発生した渦は運動成分よりも温度の方が早く周囲に拡散していく」ということを具現化しているとのことです。

１．５　p_rgh　修正圧力

　重力による圧力を除去した圧力を示しており、以下の式で定義されます。

　　　p_rgh = p – ρgh

　重力が無視出来る場合はp_rgh=pとなります(下図：サーボ・モータ熱解析結果)。

　本パラメータもopenFoamソルバ内で自動計算されますが、初期値「0」を設定する必要があります。初期設定ファイルを省略するとchtMultiRegionFoam実行でエラーとなります。

１．６　cellToRegion

　chtMultiRegionFoamのフォルダの要所要所にcellToRegionというファイルが見られますが、これはコマンド「splitMeshRegions -cellZones -overwrite」によって自動生成されるので事前に用意する必要はありません。

---

２．パラメータ・スタディ

２．１　モデル設定

　乱流強度1％、5%、10％でのｋに対するパラスタを実施してみます。

「計算モデル」(OpenFoamを用いた2D円柱周りの流体解析と同じ)

〇メッシュ設定

・円柱直径1m

・メッシュ：16(長さ) x 6(高さ) x0.04(幅)mを160x60x1の合計9600マスに分割。

・円柱表面のメッシュ粗さはrefinementSurfaces level(0 2)に設定。

 （円柱表面を基本メッシュの20～22に分割）

・円柱周辺の1.5ｍ(長さ)ｘ1.5ｍ(高さ)の区間をrefinementRegions levels(1E15 1)に設定。

　（円柱周辺を基本メッシュの21に分割）

・extrudeMeshコマンドを用いて全領域を1層に修正。

〇Openfoam設定

・積分幅5msec、積分時間100sec

・周囲速度1m/s、上下面はslip条件、円柱表面を0m/s。

・空気動粘性：2.0e-5 m2/s

・解析ソルバーはpisoFoam(非圧縮・非定常乱流解析ソルバー)

・乱流モデルはRAS(レイノルズ平均に基づく乱流モデル)でkEpsilonモデル(標準ｋ-εモデル)

・epsilonは1.2項に示す方法で設定。

・nut初期値は0。

 上記以外のパラメータは以下のOpenFoamチュートリアルの物をそのまま使用。

    tutorials\incompressible\pisoFoam\RAS\cavity

２．２　計算結果

　計算結果を以下に示します。結果、ｋの値(乱流強度)によらず圧力、速度、ｋの様子はほぼ一致しています。つまり初期条件はそこそこ合わせれば計算過程でそれなりに落ち着くようです。

（注意：kとεの関係を1.2項に合わせないと計算結果が大分変化しました）

　

〇乱流強度1％

　設定値：k=0.00015、ε=4.3e-6

　計算結果：Cd=1.0、ｙ+=83.9

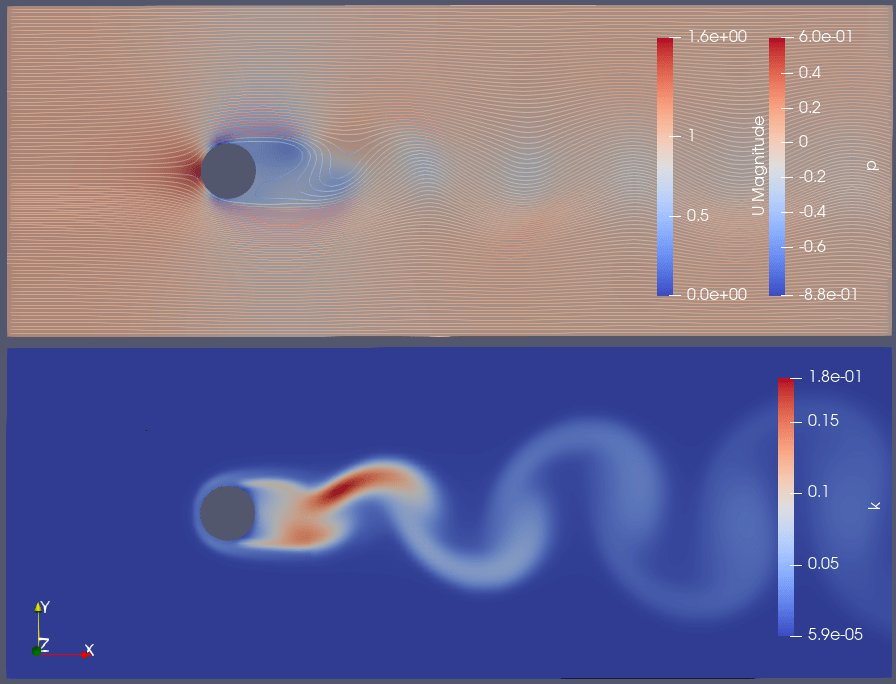
〇乱流強度5％

　設定値：k=0.00375、ε= 5.4e-4

　計算結果：Cd=0.93、y+=91.5

〇乱流強度10％

　設定値：k=0.015、ε=4.3e-3

　計算結果：Cd=0.85、y+=98.6

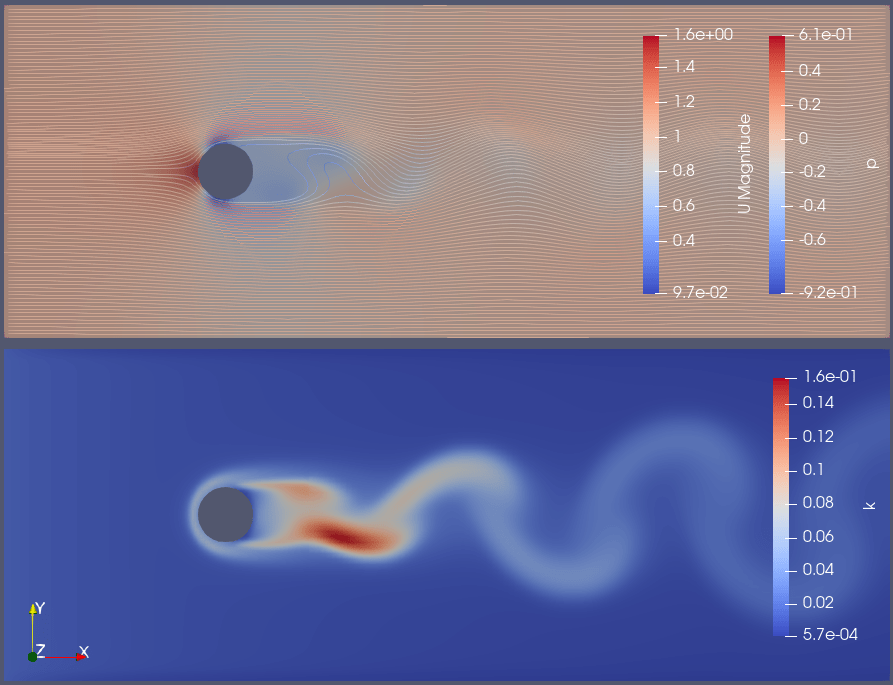
　但し計算の目的である抵抗係数Cdはそれなりに変化してしまっています(乱流強度10％ではCd=0.85となり他計算値であるCd=1.0よりも有意に小さくなってしまいました)。これは乱流境界層に初期値として乱流成分ｋを与えてしまうため、境界層が発達してしまうためと推定します。具体的には円柱背面の本来境界層が発達しそうもないところに乱流成分を与えることで剥離点が円柱後方に後退したためと推定します。　この結果からk及びεの初期値は予定される値に対し、ある程度少ない値に設定しておくことが得策と考えます。

---