鶏むね肉は低価格で脂肪分も少なくヘルシーな食材なのですが、鶏肉ゆえに火を十分通す必要があります。厚生省は「肉の深部で75℃、1分以上の加熱」を推奨しています。
個人的に料理をしてきた経験上、厚み3cm位のむね肉の塊をフライパンで蒸し焼きした場合、10分では深部がなんとなく生色でした。15分後には深部でも十分火が通りました。
このあたりをOpenFoamにて解析してみようと思います。

尚この料理の工程を一応示しておきます。
・フライパンにサラダ油を敷き、むね肉の両面を軽く焦げ目がつくまで焼きます。
・フライパンに水+みりん+お酒(肉が5mm程度浸される量)を加えて蓋をして蒸します。
・15分間蒸します。随時水を追加しないと空焚きになります。
・蓋を除き醤油等の調味料を足して煮詰めていき、両面を再度焦げ目がつくまで焼いて完成です。
尚調理器具等条件が違いますので、各人におかれましては火の通りを十分ご確認下さい。
1.1 モデル設定
鶏むね肉の寸法を設定します。

解析空間
・メッシュ:260(長さ) x 80(高さ) x200(幅)cmを13x4x10の合計520マスに分割。
・鶏むね肉まわりのメッシュ粗さはrefinementSurfaces level(1 2)に設定(基本メッシュの21~22に分割)。
・上面端に半径3cmの1/4円の排出孔を設定。
結果、出来上がったメッシュが以下の図となります(最小5mm四方)。
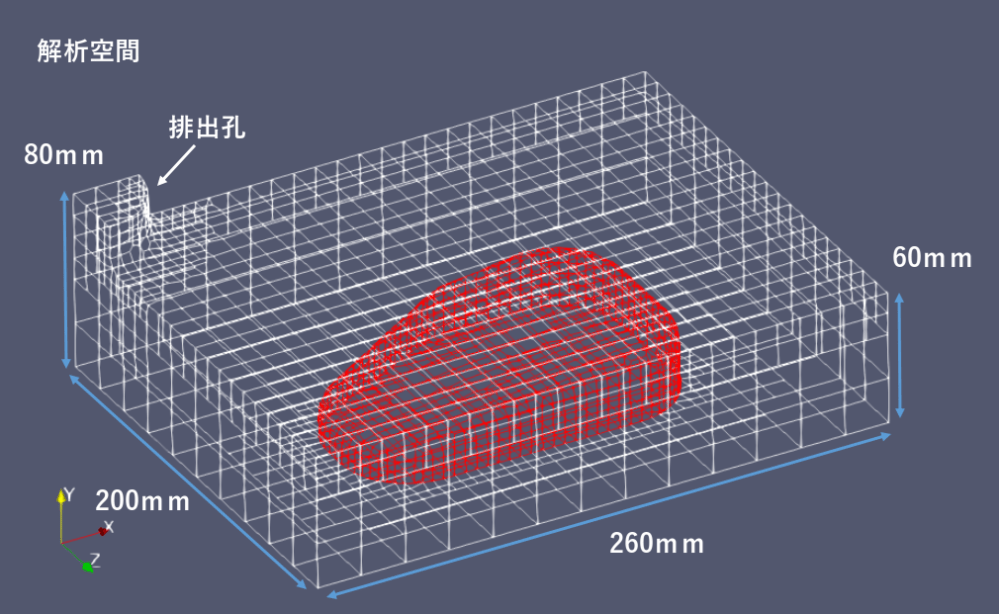
2. OpenFoam設定
Openfoamの設定を以下に示します。
・鶏むね肉材料特性:ほぼ水分としてそれ以外の成分比で以下を設定
熱伝導率:0.5[W/m/K]
比熱:3300[J/kg/K]
密度:10.5[kg/m3](実際の1/100に設定:温度収束時間を1/100にするため)
モル重量:40000[g/mol](適当:たんぱく質で代表。計算には使われていないと考える)
・蒸気特性:比熱以外を空気と同じに設定
比熱:1000000[W/m/K](空気の1000倍:1.3項にて説明)
粘性係数:1.8e-5[Pa・s]
プラントル数:0.7
モル重量:28.9[g/mol]
・鶏むね肉底面を400K(約130℃)に固定
(鍋底を想定:中火160℃と蒸気100℃の中間)。
・鶏むね肉初期温度は280[K](約10℃)に設定。
・蒸気初期温度は370[K](約100℃)に設定。
・解析空間底面の蒸気の初速を0.1[m/s]に設定。出口を除き、他の面は0[m/s]に固定。出口は計算任せ。
・圧力:全域初期値1e+5[Pa]に設定。
・解析ソルバーはchtMultiRegionFoam(pimpleアルゴリズム)
・乱流モデルはRAS(レイノルズ平均に基づく乱流モデル)でkEpsilonモデル(標準k-εモデル)。
これに伴い乱流粘性係数nutファイルを追加。
(チュートリアルはlaminar設定ですが、当事業所でソースコードを理解することなく切り替えました)
・乱流エネルギーk、乱流散逸率epsilonの初期値は[k=1.5e-6、epsilon=1.44e-7]と設定(設定根拠はこちらを参照方)。
上記以外のパラメータは以下のOpenFoamチュートリアルの物をそのまま使用。
tutorials\heatTransfer\chtMultiRegionFoam\snappyMultiRegionHeater
3. 凝縮現象における熱伝達率
蒸気(水蒸気)が低温の固体表面や液体表面に触れると液体に戻り、潜熱(凝縮潜熱)放出され、熱が伝達されます。この様子を凝縮と呼ぶそうで、この際の熱伝達率は気体(空気)に対して数桁違うようです。
今回の鶏むね肉の調理をOpenFoamにて解析する際、chtMultiRegionFoamには凝縮現象を模擬していません。そこでこのあたりを数式で確認し、なんとかchtMultiRegionFoamの既存パラメータの修正で代用を試みます(当事業所オリジナル)。
層流膜状凝縮理論のヌセルト解析では固体表面(垂直面)に生成される液膜(水)の厚さδを以下の式で表現しています(参考文献[1]5.8章)。

δ={[4kℓνℓ(Tsat-Tw)x]/[ρℓgL1ν]}1/4 ・・・(1)
kℓ:液体の熱伝導率(水の場合:0.652[W/m/K])
νℓ:液体の動粘度(水の場合:0.457e-6[m2/s])
Tsat:飽和温度(水の場合:約370[K])
Tw :固体表面温度(今回は280[K]と設定)
x :液膜付着開始点からの距離
ρℓ:液体の密度(水の場合:981.9[kg/m3])
g :重力定数9.807[m/s2]
L1ν :蒸気の凝縮潜熱(水の場合:2256.9[kJ/kg])
この時、点xにおける局所熱伝達率hxは以下の式となります。
hx=kℓ/δ ・・・(2)
鶏むね肉の代表高さb=3cmにおける平均熱伝導率を計算するため(1)式の平均を計算します。
δ=1/b*∫{[4kℓνℓ(Tsat-Tw)x]/[ρℓgL1ν]}1/4 dx
=1/b*C*∫x1/4dx=1/b*C*4/5*b5/4=(4/5)*{[4kℓνℓ(Tsat-Tw)b]/[ρℓgL1ν]}1/4 ・・・(3)
=0.088mm
よって熱伝達率hxは以下のような簡略が可能と考えます。
hx = kℓ/δ = 7390[W/m2/K] ・・・(4)
一方凝縮がない場合の熱伝達率は円柱周りの熱伝達率の下式を代表として用いることとします(参考文献[1]3.5章)。
(chtMultiRegionFoamが下式と概ね同じ様相を呈することを円柱周りの解析にて確認しています)
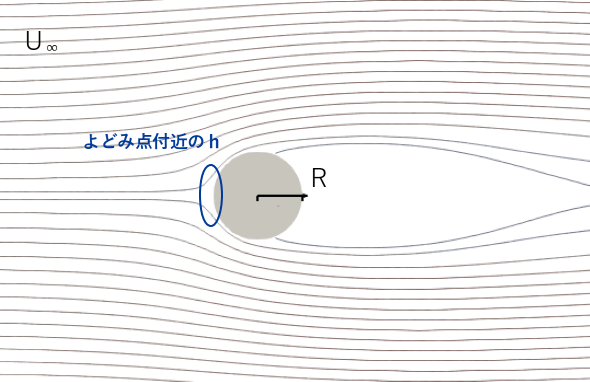
h=0.57*Pr0.385 *k/R*(2*R*U∞/ν)1/2・・・(5)
Pr:プラントル数 空気0.7
k:熱伝導率 空気0.0286[W/m/K]
R:鶏むね肉代表長さの半分として75[mm]
U∞:遠方周囲流速0.15[m/s]
(Openfoam解析結果より初期速度0.1[m/s]から
0.3[m/s]程度に増速。円周模擬のため半分とした)
ν:動粘性 空気2e-5 [m2/s]
∴h=0.57*0.70.385 *0.0286/0.075*(2*0.075*0.15/2e-5)1/2*0.5(※1)=3.18[W/m2/K] ・・・(6)
※1:上式(5)はよどみ点での熱伝達率であり、側面ではおよそ半分程度に落ち込むようです。
結果、蒸気の有無で熱伝達率は約2300倍の差があることが推定され、これは一般工学書の記述と桁が一致します。
hx:h = 7390 : 3.18 ≒ 2300
今回の計算では切りよく1000倍とします(注目する場所が肉上面で、水平のため半分位とした)。
これをOpenFoamの熱流体計算に取り込みたいのですが、chtMultiRegionFoamソルバーではフーリエの法則に基づく熱流束連続条件の式を用いており、熱伝達率の式を使用していないようです(openfoamwiki.netより)。つまりOpenfoamでは熱伝達率計算式のような理論計算ではなく、あくまで固体表面と周りの空気の間の熱伝導式を時々刻々計算してるそうです。
そうなると上記(4)(6)の計算結果をOpenFoamに取り込むことは出来ません。この解決案として物理的には意味のない式の修正を行って、熱流体計算をトライしてみます(当事業所オリジナル)。
具体的にはフーリエの式に出てくる熱伝導率を1000倍にしてみたいと考えます。ところがOpenFoamのchtMultiRegionFoamソルバーの空気側熱特性ファイルには熱伝導率が定義されていなく、その代わりに以下が定義されています。
Cp:比熱 1000[J/kg/K]
mu:粘性係数1.8e-5[Pa・s]
Pr:プラントル数 0.7
よってOpenFoamでは以下の式より熱伝導率を求めていると推定されます。
ka=mu*Cp/Pr :プラントル数の定義式
このkaを1000倍にしたい訳ですが、粘性係数1000倍は流体計算に影響が大きすぎるため、プラントル数1/1000または比熱1000倍を考えます。どちらも熱拡散に用いられているため、影響は同じと考え、ここでは比熱1000倍を選びました(いずれを選んでも物理的にあり得ない状況です)。
4. 計算結果
900秒後の計算結果を示します。
肉表面は温度を、壁は中央断面温度をずらして表示しました。 また流線は速度を示しています。

・およそ全体が蒸気温度370K(100℃)に達しています。
・出口での流速6.4[m/s]と底面初期速度0.1[m/s]はそれぞれの面積(底面393cm2:出口7.0cm2)の比56に
およそ一致します(この相違は出口速度のムラに依存していると考えられます)。
次に加熱開始より5分、10分、15分後の断面を示します(上から順に5,10,15分経過時)。
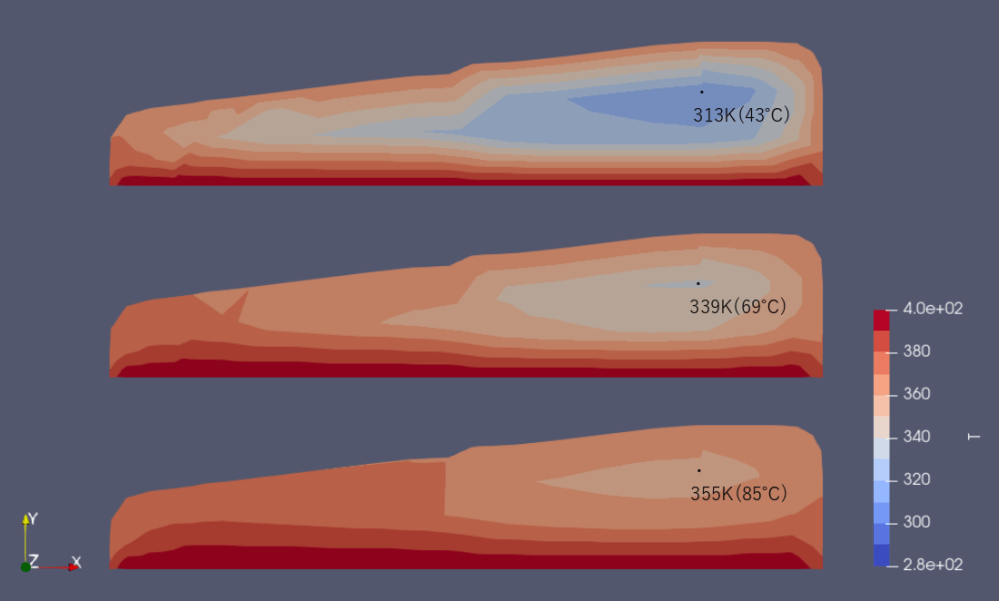
・5分では肉の深部は40℃程度でまだまだ火が通っていません。
・10分後でも深部は70℃程度で十分ではありません。
・15分後では深部でも80℃に達しており、安全に食べることが出来ると考えます。
以上OpenFoamによる計算結果は鶏むね肉調理の実経験とよく一致しました。
「計算条件の振り返り」
・レイノルズ数Re=0.15[m/s]*0.15[m]/ 2e-5 = 1125:乱流モデルはlaminarでも良かったようです。
・積分幅 0.1msec(クーラン数2e-3):Cp1000倍による計算発散を防ぐため、積分幅を小さくしました。
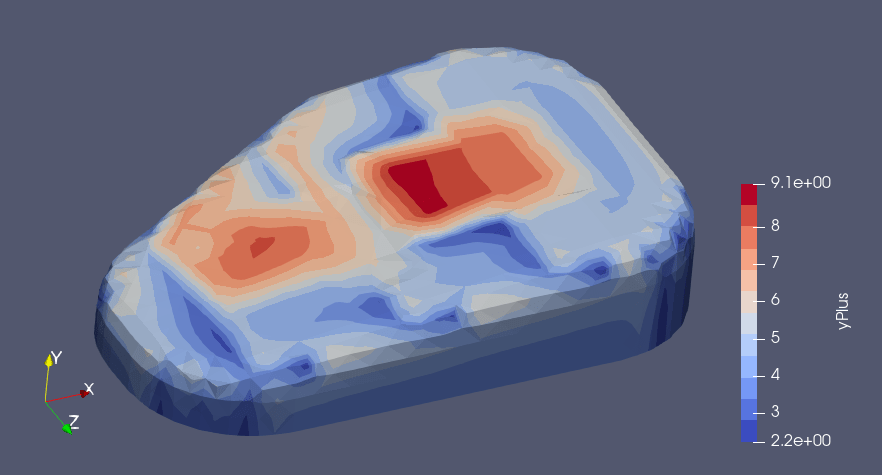
・壁関数の計算結果は下図(最大9.1、最小2.2)でこれもRASの適切範囲(30~1000)の領域外でした。
もう少しメッシュを大きくする必要があるようです。
「注意点」
本計算では以下の大きな仮定のもと、計算を実施しており実際現象への適応は試験値との比較が重要となります。
・肉の熱伝導率は肉質、温度により相当なばらつきがあるようです。
・肉の比熱を一定値としています(実際には火が通りだすとタンパク質の変性が発生し、物性値が変化する)。
・比熱を1000倍に修正しているため、流体計算に少なからず影響を与えています。
・比熱1000倍という数値自身も2300倍からの適当な設定です。
参考に比熱1倍(無修正)の時の計算結果を以下に示します。気体流れに関しては無修正の方が若干遅くなっているようです(最大速度Cp1000倍6.4[m/s]、Cp無修正5.7[m/s])。

参考文献
[1]JSMEテキストシリーズ 伝熱工学 日本機械学会 丸善出版
