「テーマ」
・OpenFoam円柱周りの熱伝導の解析結果を実験値と比較する。
「方針」
・幾つかのレイノルズ数において2D円柱周りの熱流体解析をRAS※1で実施し、実験値と比較する。
「背景」
・サーボ・モータの解析にて熱伝導率の実験式と挙動が一致しなかった(実験式からは熱伝導率は速度の平方根に比例)。
・使用した乱流モデルはlaminar(層流)用で、低レイノルズ数にしか対応出来ない。
・乱流モデルをRASにすることで適用出来るレイノルズ数を上げようと試みる。
※1 RAS:Reynolds Averaged Simulationの略。RANSと同じ。
1.1 モデル設定
下記のような2D円柱を設定します。
・円柱直径10cm
・メッシュ:110(長さ) x 60(高さ) x1(幅)cmを55x30x1の合計1815マスに分割。
・円柱表面のメッシュ粗さはrefinementSurfaces level(0 1)に設定。
(円柱表面を基本メッシュの20~21に分割)
結果、出来上がったメッシュが以下の図となります(最小1cm四方)。

1.2 OpenFoam設定
Openfoamの設定を以下に示します。
・円柱の材質は銅。
・銅の密度を8960[kg/m3]から89.6[kg/m3]に変更。これにより温度収束時間は1/100となる。
・円柱上下面からそれぞれ2[W]で加熱。
・初期温度は全て300[K]
・周囲速度0.1、1、10、40m/sの4ケース、上下面はslip条件、円柱表面を0m/s。
・疑似2Dとするため厚み方向の面はsymmetryPlaneと設定。
・圧力:出口をゲージ圧1e+5で固定
(この方が安定します。但し円柱後流領域を十分取る必要があります)。
・空気動粘性:2.0e-5 m2/s
・熱流束q[W/m2]は追加機能関数wallHeatFluxを使用。
・解析ソルバーはchtMultiRegionFoam(pimpleアルゴリズム:OpenFoamユーザーガイド)
・乱流モデルはRAS(レイノルズ平均に基づく乱流モデル)でkEpsilonモデル(標準k-εモデル)。
これに伴い乱流粘性係数nutファイルを追加。
(チュートリアルはlaminar設定ですが、当事業所でソースコードを理解することなく切り替えました)
・乱流エネルギーk、乱流散逸率epsilonの初期値は[k=0.1、epsilon=0.01]を基本とし、適宜調整。大きすぎると解析空間が不安定、小さすぎると乱流成長せず。
上記以外のパラメータは以下のOpenFoamチュートリアルの物をそのまま使用。
tutorials\heatTransfer\chtMultiRegionFoam\snappyMultiRegionHeater
1.3 計算結果
ケース2、3、4、1の順に計算結果を示します。
〇ケース2:周囲速度1m/s
// レイノルズ数Re=1[m/s]*0.1[m]/ 2e-5 = 5000 / 壁関数y+=平均34(適正値30~500位) //
// 積分幅 2e-3秒(クーラン数0.2) / 解析空間内計算時間 短縮措置で500秒(50000秒相当) //
// k=0.1、epsilon=0.01 //
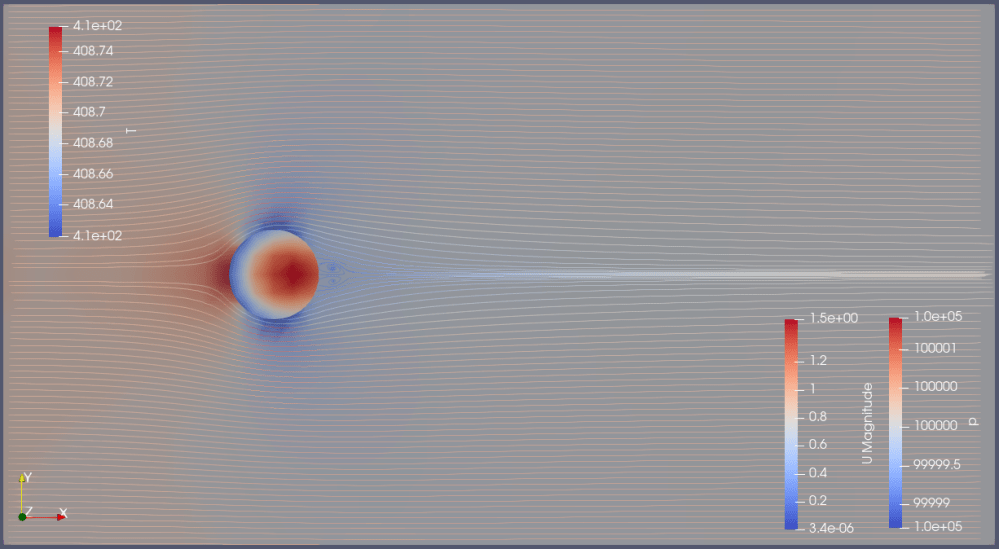
・周囲速度1m/sが円柱側面で最大1.50m/sまで増速。
・円柱温度はおよそ408.8K。前後で若干の温度差が発生。
・円柱後方に渦が見て取れる。但しカルマン渦列までは成長していない
(メッシュの粗さとpimpleFoamのために平均化されていると推定します)
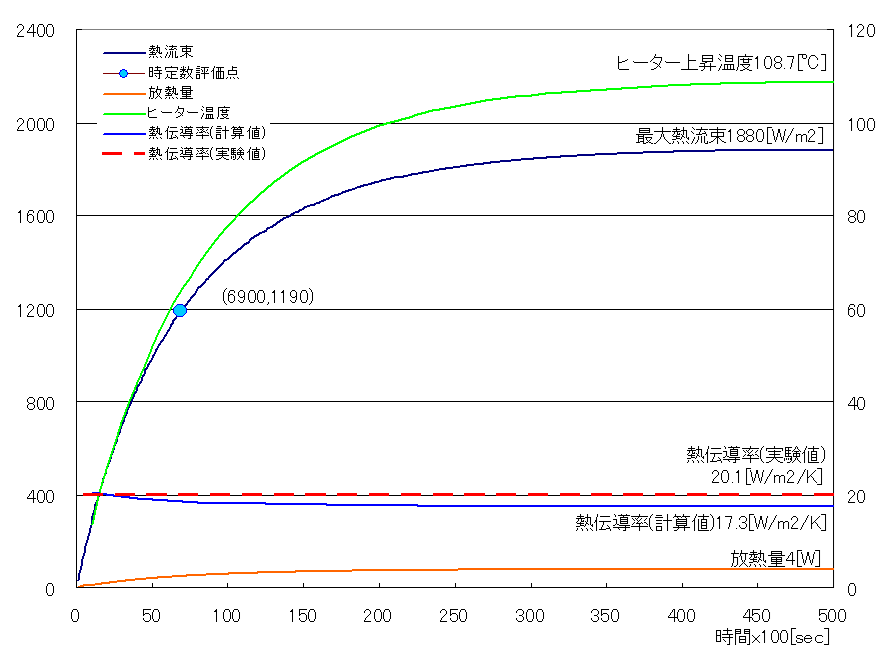
続いて熱伝導の様子をグラフに示します。
・放熱量4[W]は加熱量4[W]と一致。
・熱伝導率(計算値)17.3[W/m2/K]※4は熱伝導率(実験値)20.1[W/m2/K]※1と大体一致。
・収束温度108.7℃と熱伝導率(計算値)17.3[W/m2/K]より求められる放熱面積は
円柱側面積の68%※2。
・熱流束曲線から得られる時定数約6900秒と計算値7950秒※3が大体一致。
周囲速度1m/sで直径10cmの円柱に対し大体実験値との一致を得られました。
※1 熱伝導率h[W/m2/K]=20.1(実験値)
h=0.57*Pr0.385 *k/R*(2*R*U/ν)1/2 :参考文献[1]の3.4.2項より
Pr:プラントル数 空気0.7
k:熱伝導率 空気0.0286W/(mK)
R:円柱半径 5mm
U:遠方周囲流速 1m/s
ν:動粘性 空気2e-5 m2/s
※2 収束温度ΔT=Qin/hs=108.7℃(計算値)
Qin:加熱量 4[W]
∴ s=4/17.3/108.7=2.13e-3(円柱側面積の68%)
※3 時定数τ=cρV/hs=7950秒
c :銅比熱 419[J/kg/K]
ρ:銅密度 8900[kg/m3]
s :冷却面積 2.13e-3(上記計算値)
※4 熱伝導率(計算値) OpenFoam関数wallHeatFluxを用いて熱流束q[W/m2]の最大値を計算。
その値を円柱平均温度で割った。上記※1の実験値よどみ点近傍の値に対応する。
〇ケース3:周囲速度10m/s
// レイノルズ数Re=10[m/s]*0.1[m]/ 2e-5 = 50000 / 壁関数y+=平均221(適正値30~500位) //
// 積分幅 2e-4秒(クーラン数0.2) / 解析空間内計算時間 短縮措置で150秒(15000秒相当) //
// k=0.1、epsilon=0.01 //
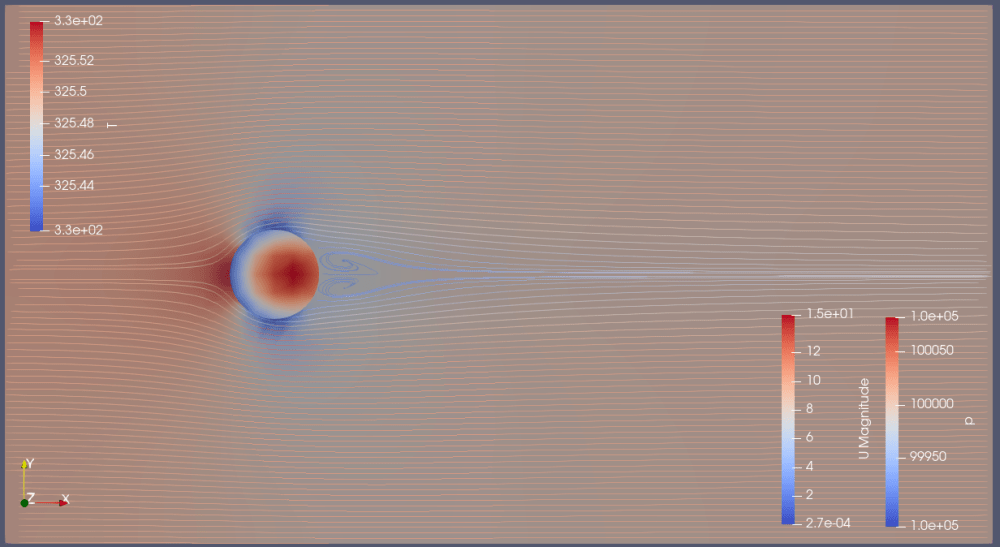
・周囲速度10m/sが円柱側面で最大14.6m/sまで増速。
・円柱温度はおよそ325.5K。前後で若干の温度差が発生。
・円柱後方に渦が見て取れる。但しカルマン渦列までは成長していない
続いて熱伝導の様子をグラフに示します。
・放熱量4[W]は加熱量4[W]と一致。
・熱伝導率(計算値)69.3[W/m2/K]は熱伝導率(実験値)63.6[W/m2/K]※1と大体一致。
・収束温度25.5℃と熱伝導率(計算値)69.3[W/m2/K]より求められる放熱面積は円柱側面積の72%※2。
・熱流束曲線から得られる時定数約1900と計算値1870※3が大体一致。
周囲速度10m/sで直径10cmの円柱に対し大体実験値との一致を得られました。これは一般生活に活かせそうなレベルと考えます。

※1 熱伝導率h[W/m2/K]=63.6(実験値)
h=0.57*Pr0.385 *k/R*(2*R*U/ν)1/2 :参考文献[1]の3.4.2項より
Pr:プラントル数 空気0.7
k:熱伝導率 空気0.0286W/(mK)
R:円柱半径 5mm
U:遠方周囲流速 10m/s
ν:動粘性 空気2e-5 m2/s
※2 収束温度ΔT=Qin/hs=25.5℃(計算値)
Qin:加熱量 4[W]
∴ s=4/69.3/25.5=2.26e-3(円柱側面積の72%)
※3 時定数τ=cρV/hs=1870秒
c :銅比熱 419[J/kg/K]
ρ:銅密度 8900[kg/m3]
s :冷却面積 2.26e-3(上記計算値)
〇ケース4:周囲速度40m/s
// レイノルズ数Re=40[m/s]*0.1[m]/ 2e-5 = 200000 / 壁関数y+=平均162(適正値30~500位) //
// 積分幅 5e-5秒(クーラン数0.4:最小メッシュ5mm四方に変更) //
// 解析空間内計算時間 短縮措置で60秒(6000秒相当) //
// k=0.01、epsilon=0.01 //
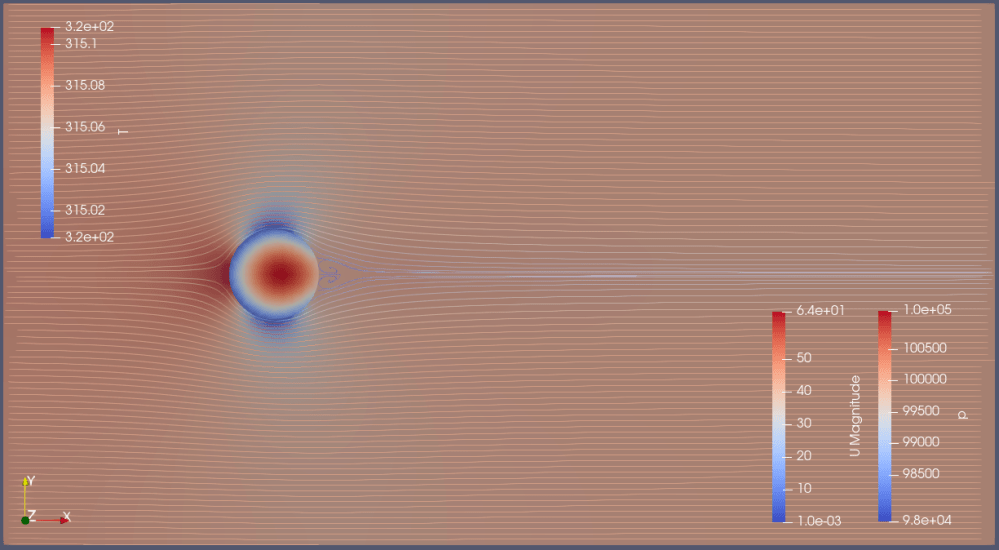
・周囲速度40m/sが円柱側面で最大64.3m/sまで増速。
・円柱温度はおよそ315.1K。前後で若干の温度差が発生。
・円柱後方に渦が見て取れる。但しカルマン渦列までは成長していない
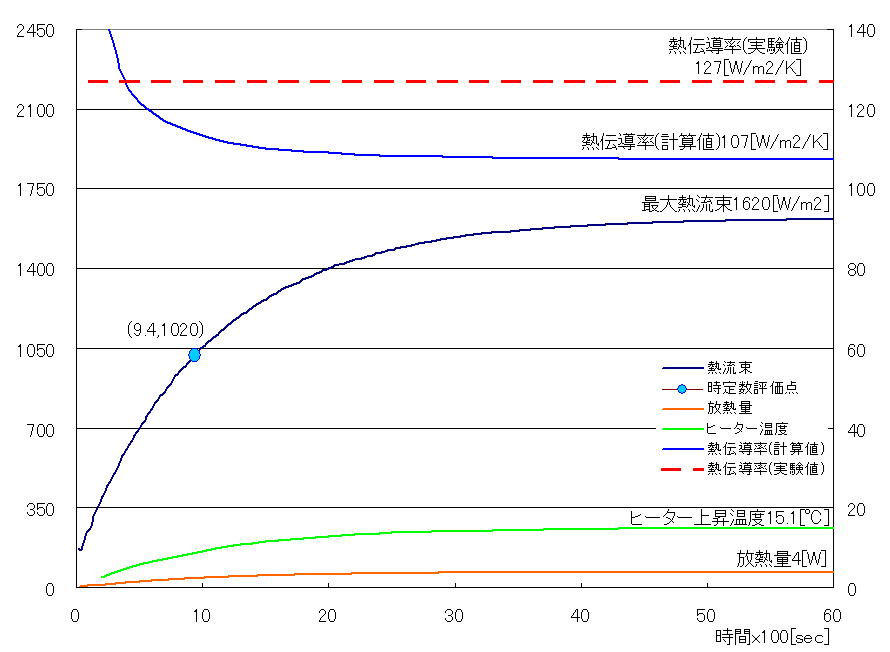
続いて熱伝導の様子をグラフに示します。
・放熱量4[W]は加熱量4[W]と一致。
・熱伝導率(計算値)107[W/m2/K]は熱伝導率(実験値)127[W/m2/K]※1と大体一致。
・収束温度15.1℃と熱伝導率(計算値)107[W/m2/K]より求められる放熱面積は円柱側面積の79%※2。
・熱流束曲線から得られる時定数約1020秒と計算値1100秒※3が大体一致。
周囲速度40m/sで直径10cmの円柱に対し大体実験値との一致を得られました。 またレイノルズ数2*10^5は亜臨界上限であり、ここまで一致すればRASによるpimpleFoamでは十分と考えます(1.4項にて後述)。
※1 熱伝導率h[W/m2/K]=127(実験値)
h=0.57*Pr0.385 *k/R*(2*R*U/ν)1/2 :参考文献[1]の3.4.2項より
Pr:プラントル数 空気0.7
k:熱伝導率 空気0.0286W/(mK)
R:円柱半径 5mm
U:遠方周囲流速 40m/s
ν:動粘性 空気2e-5 m2/s
※2 収束温度ΔT=Qin/hs=15.1℃(計算値)
Qin:加熱量 4[W]
∴ s=4/107/15.1=2.48e-3(円柱側面積79%)
※3 時定数τ=cρV/hs=1100秒
c :銅比熱 419[J/kg/K]
ρ:銅密度 8900[kg/m3]
s :冷却面積 2.48e-3(上記計算値)
〇ケース1:周囲速度0.1m/s
// レイノルズ数Re=0.1[m/s]*0.1[m]/ 2e-5 = 500 / 壁関数y+=平均3.4(適正値30~500位) //
// 積分幅 2e-2秒(クーラン数0.2) / 解析空間内計算時間 短縮措置で1500秒(150000秒相当) /
// k=0.01、epsilon=0.001 //
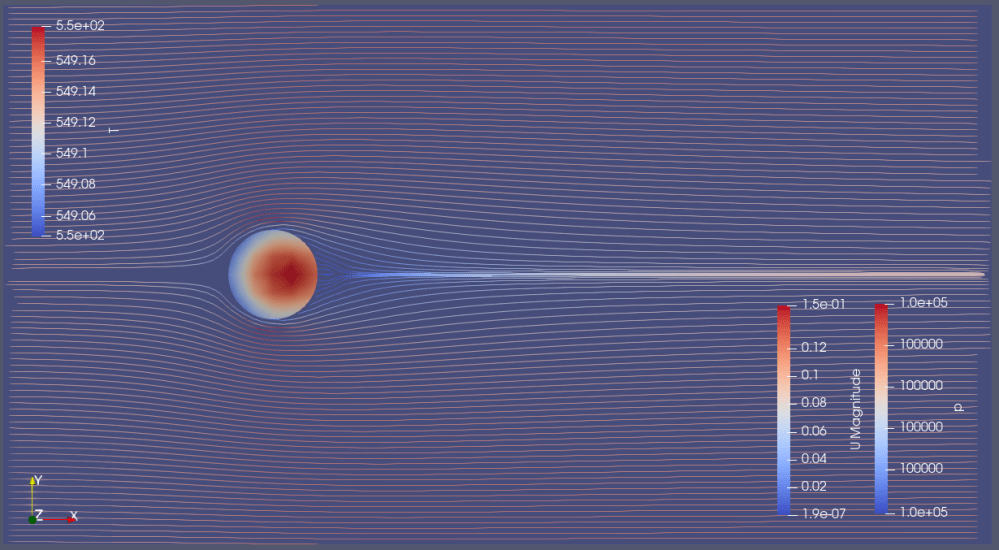
・周囲速度0.1m/sが円柱側面で最大0.15m/sまで増速。
・円柱温度はおよそ549.2K。前後で若干の温度差が発生。
・円柱後方に渦が見て取れる。但しカルマン渦列までは成長していない
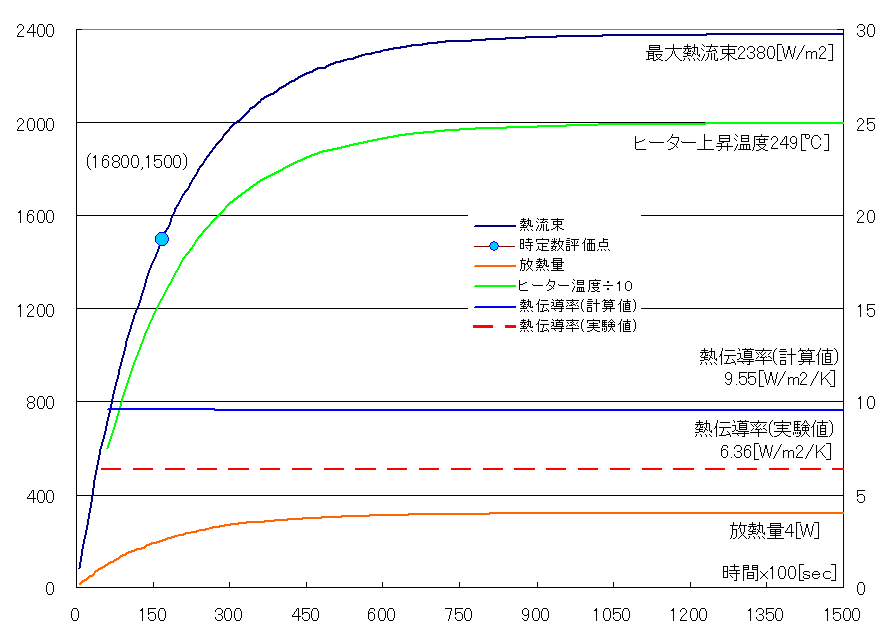
続いて熱伝導の様子をグラフに示します。
・放熱量4[W]は加熱量4[W]と一致。
・熱伝導率(計算値)9.55[W/m2/K]は熱伝導率(実験値)6.36[W/m2/K]※1と他ケースに比べるとずれている。
・収束温度15.1℃と熱伝導率(計算値)9.55[W/m2/K]より求められる放熱面積は円柱側面積の54%※2。
・熱流束曲線から得られる時定数約16800秒と計算値18300秒※3が大体一致。 しかしそもそもレイノルズ数500という低い領域を乱流モデル(RAS)で且つ壁関数y+=3.4では無理があるかもしれません。
※1 熱伝導率h[W/m2/K]=6.36(実験値)
h=0.57*Pr0.385 *k/R*(2*R*U/ν)1/2 :参考文献[1]の3.4.2項より
Pr:プラントル数 空気0.7
k:熱伝導率 空気0.0286W/(mK)
R:円柱半径 5mm
U:遠方周囲流速 0.1m/s
ν:動粘性 空気2e-5 m2/s
※2 収束温度ΔT=Qin/hs=249℃(計算値)
Qin:加熱量 4[W]
∴ s=4/9.55/249=1.68e-3(円柱側面積の54%)
※3 時定数τ=cρV/hs=18300秒
c :銅比熱 419[J/kg/K]
ρ:銅密度 8900[kg/m3]
s :冷却面積 1.68e-3(上記計算値)
1.4 計算結果の考察
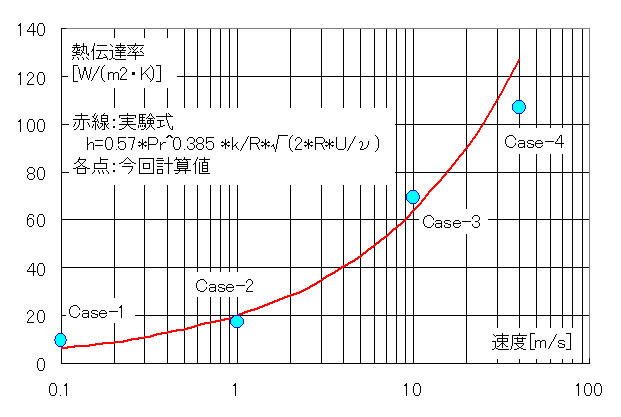
detail2では出来なかった速度の平方根に比例した熱伝導率の変化を再現出来きました(下図)。
また冷却面積を円柱周り面積の割合で示したが、これはdetail2で示した有効面積倍数に相当します。
よって今回と同じ方法でサーボ・モータの冷却解析が出来る目途が立ちました。
尚ここで計算した熱伝達率は局所的な最大値であり、計算上下図(ケース2での熱伝達率の分布。単位は[W/m2/K])のように分布しています(実際も分布しているそうです(参考文献[1]3.4.2項))。 主に円柱前面で放熱され、円柱背面での放熱はかなり少ない様子です。このため円柱背面は前方に比べ高温になるのだと考えられます。

一方本計算過程から以下の注意点を認識しました。
・円柱解析で示した通り、レイノルズ数2e+5以下ではカルマン渦列が円柱後方に発生します。しかしpimpleFoamのRASモデルでは発生していません。剥離点が円柱背面側まで移動しており、あたかも超臨界領域の挙動を示しています。
(超臨界では円柱前方に乱流境界層が現れ、剥離を遅らすそうです。)
(但し1.3項の計算(pimpleFoamのRASモデル)では円柱前方に乱流境界層はk値からは見て取れませんでした。)
・この影響(剥離点が後退)として実際は冷却効率が1.3項で示したものよりも下がる可能性があります。
ケース2からケース4までの冷却面積は円柱側面積の68~79%で、これは角度にすると122~142°に対応し超臨界での剥離点に対応しています。亜臨界での剥離点は一般的に80°位だそうで、例えばケース3の剥離点130°が80°まで前進すると最大62%(=80/130)の冷却ダウンの可能性があると考えます。
円柱側面積比(剥離点角度)
ケース1:0.1m/s 54%(97°)
ケース2: 1m/s 68%(122°)
ケース3:10m/s 72%(130°)
ケース4:40m/s 79%(142°)
実験ではレイノルズ数が臨界領域(2e+5~2e+6)では一旦抵抗係数が下がり、超臨界(2e+6以上)では再び抵抗係数が増加するそうです(円柱解析)。超臨界でのカルマン渦列は更に不規則なるそうで、このレベルを模擬することは当事業所のパソコン・レベルでは難しい領域と考えられます。
参考文献
[1]JSMEテキストシリーズ 電熱工学 日本機械学会 丸善出版
