「テーマ」
・OpenFoam円柱周りのCd及びストロ-ハル数の解析結果を実験値と比較する。
「方針」
・幾つかのレイノルズ数において2D円柱周りの流体解析をRAS※1で実施し、実験値と比較する。
※1 RAS:Reynolds Averaged Simulationの略。RANSと同じ。
1.1 モデル設定
下記のような2D円柱を設定します。
・円柱直径1m
・メッシュ:16(長さ) x 6(高さ) x0.04(幅)mを160x60x1の合計9600マスに分割。
・円柱表面のメッシュ粗さはrefinementSurfaces level(0 2)に設定。
(円柱表面を基本メッシュの20~22に分割)
・円柱周辺の1.5m(長さ)x1.5m(高さ)の区間をrefinementRegions levels(1E15 1)に設定。
(円柱周辺を基本メッシュの21に分割)
結果、出来上がったメッシュが以下の図となります。

1.2 OpenFoam設定及び計算結果(その1)
Openfoamの設定を以下に示します。
・周囲速度0.01、0.1、1、5、10m/sの5ケース、上下面はslip条件、円柱表面を0m/s。
・圧力:出口をゲージ圧0で固定
(この方が安定します。但し円柱後流領域を十分取る必要があります)。
・空気動粘性:2.0e-5 m2/s
・抵抗係数Cdの計算は追加機能関数forceCoeffsを使用。
・解析ソルバーはpisoFoam(非圧縮・非定常乱流解析ソルバー)
(もう一つの非圧縮・非定常ソルバーであるpimpleFoamではカルマン渦発生と共にCdが振動しながら実験値から外れていきました。)
・乱流モデルはRAS(レイノルズ平均に基づく乱流モデル)でkEpsilonモデル(標準k-εモデル)
・epsilon、k及びomegaの初期値は参考文献[1]4.5.5章の計算値の約1/5を設定。
・nutの初期値は0とし、nuTildaは無視(使われていない。たぶんomegaも使われていない)。
上記以外のパラメータは以下のOpenFoamチュートリアルの物をそのまま使用。
tutorials\incompressible\pisoFoam\RAS\cavity
ケース別に計算結果を以下に示します。
〇ケース1:周囲速度0.01m/s(レイノルズ数500)
積分幅 5e-1秒(クーラン数0.1) / 解析空間内計算時間 12000秒 / Y+(円柱周り) Ave 1.73
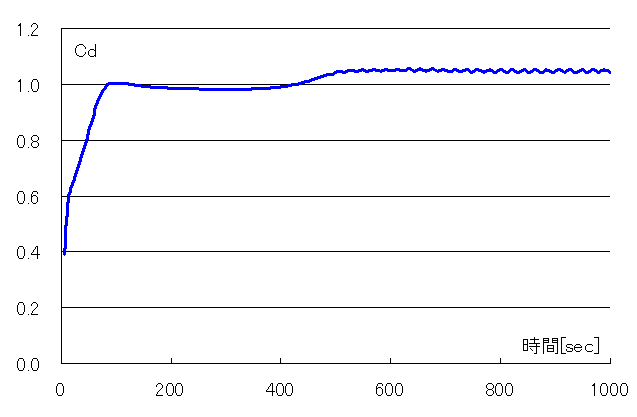
結果、Cd=1.21、ストロ-ハル数=1/4.1=0.24(直径と山間の距離の比)
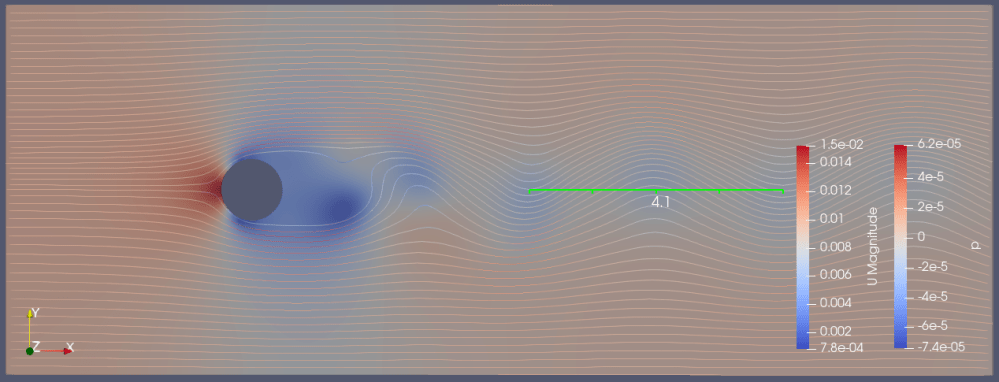

〇ケース2:周囲速度0.1m/s(レイノルズ数5000)
積分幅 5e-2秒(クーラン数0.1) / 解析空間内計算時間 1000秒 / Y+(円柱周り) Ave 7.03
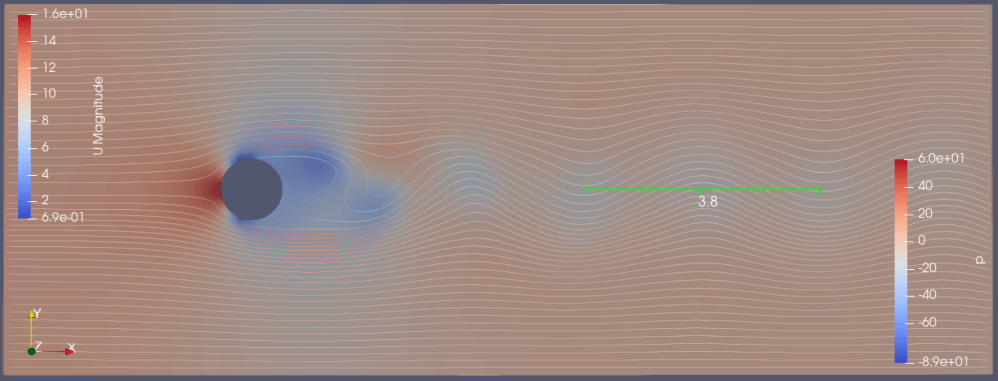
結果、Cd=1.05、ストロ-ハル数=1/3.9=0.26

〇ケース3:周囲速度1m/s(レイノルズ数5e+4)
積分幅 5e-3秒(クーラン数0.1) / 解析空間内計算時間 100秒 / Y+(円柱周り) Ave 83.9
結果、Cd=1.02、ストロ-ハル数=1/3.85=0.26


〇ケース4:周囲速度5m/s(レイノルズ数2.5e+5)
積分幅 1e-3秒(クーラン数0.1) / 解析空間内計算時間 20秒 / Y+(円柱周り) Ave 405
結果、Cd=1.01、ストロ-ハル数=1/3.7=0.27


〇ケース5:周囲速度10m/s(レイノルズ数5e+5)
積分幅 5e-4秒(クーラン数0.1) / 解析空間内計算時間10秒 / Y+(円柱周り) Ave 823
結果、Cd=0.98、ストロ-ハル数=1/3.8=0.26

1.3 計算結果の考察(その1)
(1)抵抗係数
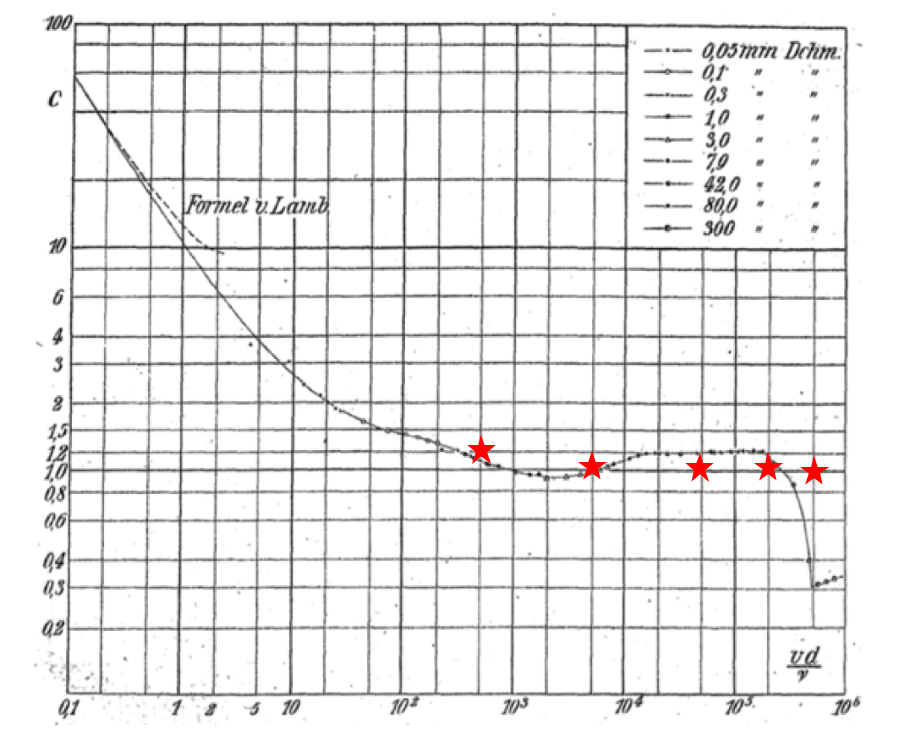
以下に1921年Wieselsbergerによって示された円柱のレイノルズ数別Cd値の実験値を示します。
その図上に今回計算した結果を赤い☆印で重ね書きします。
2*105以降の非線形部分を模擬することは出来ていないようです。
(2)ストロ-ハル数
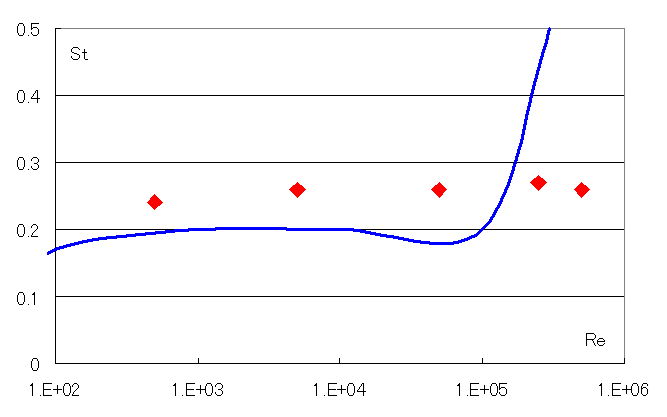
以下に幾つかの専門書に記載されている円柱のレイノルズ数別ストロ-ハル数の実験値(青線)を示します。
その図上に今回計算した結果を◆印で重ね書きします。
St = f*d/U
St:ストロ-ハル数
f :カルマン渦の振動数[Hz]
d :円柱直径[m]
U:一様流速[m/s]
全般的に若干数値が高く、また105以降の非線形部分を模擬することは出来ていないようです。
1.4 OpenFoam再設定及び再計算結果(その2)
(その1)の計算では計算積分幅をクーラン数0.1を満足する値としました。通常流体解析ではクーラン数0.6以下が望まれまており今回は十分それを満足してます。一方今回使用しているpisoFoamは乱流モデルを扱っているため更に細かいクーラン数0.01出の計算(計算積分幅を一桁小さくする)を念のため実施して見ます。
(他の設定はすべて(その1)と同じとします)
結果を(その1)と同じ実験値の図上に青い☆印で示します。

今度は105以降の非線形部分を模擬出来ているのに、他がずれてしまいました(ケース1は例外で後述します)。
この事象を詳しく見ていくためケース5の計算結果を以下に示します。
下図は解析空間で4秒経過後で、十分収束した状態です。
特徴的な点としてカルマン渦が見てとれません。専門書によると臨界レイノルズ数(2*10^5以上)では円周前方に乱流境界層が成長しその乱流境界層のおかげて円柱流れの剥離点が後退するそうです。確かに(その1)での解析では剥離点が前方80度位だったものが、下図では130度位まで後退しています。この剥離点の後退のおかげで円柱後方の背圧が低くならないで済んでいます(色が青くないです)。すなわち前後の圧力差による形状抵抗が小さくなります。

それでは乱流境界層の様子を確認してみます。
乱流境界層を可視化するためケース5のk(乱流運動エネルギー)を下図に示します。kは乱流内での平均速度からのずれ分速度による運動エネルギーを示しています。
(一般的には下式となりますがOpenFoam内での定義は未確認です)。
k= 1/2*(ux2+uy2+uz2)
ux、uy、uz:局所平均速度からのずれ速度成分
確かに円柱表面に下流と同じくらい乱れている部分(赤色)を確認出来ます。この乱流境界層のおかげで剥離が遅れるそうです。乱流は水平方向+垂直方向にも流れがあるため、円柱表面のはがれかけた気流に運動エネルギーを供給するのだそうです。但しOpenFoamがそれを模擬しているかは不明です。

またカルマン渦は外見上無くなって見えますが、渦は存在するそうです。それを可視化するためnut(乱流粘性係数)を下図に示します(乱流の影響度合いを示すもので乱流そのものではありません)。
速度流線では見えない周期的な振動が見て取れます。この図から読み取れるストロ-ハル数は1/2.1=0.48となります((その1)の計算で示した高レイノルズ数におけるストロ-ハル数の増加に対応していそうです)。

このようにケース5では積分間隔を1桁小さくすることで抵抗係数の非線形部分を模擬出来ているのですが、残念なことにケース2~4でも同じように乱流境界層が発達してしまい、抵抗係数が0.3辺りを示してしまいます。
一方ケース1では抵抗係数が実験値に近い値を示しています。ケース1での計算結果(k及びU&P)を以下に示します。
速度が遅いためk(乱流運動エネルギー)が円柱前に十分な乱流境界層を作れていないようです。
このため剥離点が前方に移動し、円柱後方の背圧が下がっています(青色になっています)。


1.5 まとめ
結論から申し上げますと1.2項(その1)と1.4項(その2)の解析結果のどちらを使うべきかは、これだけでは決められないと考えます。一般的にクーラン数を小さくする(積分幅を小さくする)方が解析精度が上がるはずなのですが、1.4項ではむしろ実験値から外れてしまいます。
(その1)では積分幅が大きすぎるため、乱流境界層が十分発達出来ず、振る舞いが層流境界層に近いものになり(剥離点が80度付近)、抵抗係数が実験値に近くなったと考えられます(但しクーラン数は0.1で一般的には十分な値です)。
一方(その2)では積分幅を細かくすることで臨界レイノルズ数辺りでは乱流境界層が発達し、剥離点を後退させたことで実験値に近くなったのだですが、それ以外の領域では実験値から離れてしまいました。(クーラン数は0.01です)。
今回の場合、検討する速度のレイノルズ数から亜臨界の場合は1.2項のクーラン数0.1を、超臨界の場合は1.4項のクーラン数0.01を用いることで実験値との一致を試みる事が必要と考えます。もちろん計算結果kを注意深く観察し、適切な乱流境界層になっているかを確認する必要があると考えます。
今後Openfoamを用いて他モデルの計算を行う際は以下の区別が必要と考えられます。
レイノルズ数 解法
~数百以下 laminar(層流)
数百~2*105 RAS(乱流)or LES(未検証)
但し乱流境界層を円柱前方で発達させないように
積分幅またはメッシュサイズで調整必要
2*105~106 RAS(乱流) or LES(未検証)
尚laminar(層流)でレイノルズ数が数百以上の計算を行っても円柱後方の圧力減少を表現出来ないため、抵抗係数が実験値と一致しません(計算値が0.3程度にしかなりませんでした)。乱流モデルは円柱後方の目に見えない渦を表現するために必要な物と考えられます(目に見えないレベルの渦が圧力損失を表現しているようです)。
以上のように複雑な事象を扱う流体解析は専門性が高く、当事業所で実施する検討は限られたレイノルズ数範囲(公知の実験値と計算値が比較可能な領域)での解析となります。
この観点から円柱周り強度計算に用いた速度70m/sはその範囲を大きく超えており、あくまで参考として計算したものであることをご了解下さい。
[追記]
① 一言でカルマン渦列と呼んでも、レイノルズ数に応じて更に小さな渦が内包されるそうです。このような乱流を扱うことはそもそも数値計算に困難な領域だそうです。粘性の影響する境界層を脱すれば、非粘性として扱うことが可能となるため、数値計算の対象となる形状が極力渦を出さないことが数値計算と実験値の一致を見れると考えます。
② RAS乱流モデルを用いる場合、メッシュは細かすぎるのもよくないそうです。一般的に壁関数y+が30~300の間に設定すべきそうです。今回の1.2項及び1.4項共にのケース1、2ではメッシュが小さすぎてy+<30となっています。
参考文献
[1]OpenFOAMによる熱移動と流れの数値解析第2版 一般社団法人オープンCAE学会編 森北出版
