1.1 想定モデル
Scilabモデルはせいぜい10x10マスのモデルであり、実際に現場で問題となる局所的な応力議論に対応出来ません。そこでFreeCADを用いて局所的な解析を試みます。
以下のような状況を想定します。若干無理くりな設定ですが、あくまで例題としてご参照下さい。

「モデル想定」
・500x500x0.5mm リベットで固定されたアルミ薄板
・直径1mの円柱に70m/s(250km/h)の気流が当たるときの風下側の気流がはがれだしているあたりにおける乱流を外力に想定。
「想定荷重」
・円柱周りの風速は70m/s(250km/h)。よって円柱後方に発生するカルマン渦の周波数は以下。
f=0.2*V/D=0.2*70m/s/ 1m = 14Hz
・風速70m/sでの動圧は1/2*1.225*702=3001Pa。このうち5%程度の変動が円柱前方で発生すると仮定すると3001*5%=150Pa(この5%に関しては当HPのOpenFoamを用いた円柱周りの流体解析をご覧ください)。
・以上より円柱後方には圧力0~150Paが14Hzの周期で付加させると仮定。
・Scilab共振解析(Step2)より、固有振動数17.16Hzに対し14Hzの加振では定常の2.99倍の共振が発生。FreeCADでは上記150Paを2.99倍することで表現する。
以上の設定からまずはstep1、step2で用いたモデルに150Pa x 2.99倍の負荷を与え、変形量と応力を計算します。結果を以下に示します。
応力σx=155MPa(最大変位43.94mm)となりました。理論値は138MPa、44.2mm(薄板解析Step2)であり、比較的一致していると考えます。

リベット周りには応力集中が発生するため上記155MPa(22.5ksi)の数倍がリベット周りに発生するものと予想されます。一方アルミ材料特性として以下を用います。仮に数倍の応力が印加されると短時間で疲労に至ることが推定されます。
アルミ2024-T42材(参考文献[1])
Ftu(引っ張り終局応力):393Mpa(57ksi)
Fty(引っ張り降伏応力):234Mpa(34ksi)
Fsu(せん断終局応力):234Mpa(34ksi)
1.2 リベットを含めた全体モデル
Step1、Step2で用いたモデルに以下のようなリベットを組み込みます。
・リベット穴数:30x4辺
・リベット穴径:#5(0.156inch)
・リベット間隔:4D(16mm)
・リベット頭径:0.312inch
・縁距離(穴中心-縁):10mm
・メッシュ:Max5mm「中程度」
・空力負荷:150Pa x 2.99倍=449Pa
・拘束条件:リベット穴120度分を拘束(次項で確認)



計算結果を以下に示します。
リベットによる固定点が内部に移動したため、変形量は39.5mmと減っています。

この変形における応力σxが以下となります(板の裏面を拡大)。

1.1項では155MPaだった応力σxが穴周りで460MPaにまで増加しています。
ただその値は拘束条件の切れ目であり、実際に考慮すべきは穴周辺の黄色の領域、約250MPaと考えられます。
この約250Mpaの根拠は以下と考えられます。
・穴周りの応力を受けている黄色の領域はリベット穴間距離4Dのおよそ1/3程度。
・図中リベット穴前方の緑色領域の応力がおよそ80MPa
・80MPaの3倍で約250MPaに達していると推察される。
1.3 局所モデル
1.2項の計算結果である250MPa荷重を、リベット周りを拡大したモデルにて更に解析してみます。
・薄板、リベット、座面を用意
・リベット穴3.9624mmに対し、リベット直径3.86mmとして100μのがたを設定。
・メッシュ:Max2mm「中程度」、2次精度なし
・接触剛性:アルミ2024-T42材のベアリング降伏応力500MPaを設定
・負荷:端部に上下155MPa(安全側として1.2項縁最大を使用)
負圧による面直方向荷重は少ないため、ここでは省略。

計算結果を以下に示します(σxを表示)。
結果、1.1項と同じにすると様相はほとんど同じとなりました。x方向リベット前後に干渉による応力が立ち、リベット側面には1.1項と同じようなテンションが発生しています。
実は1.1項でリベット一部120度分を拘束したのもこの結果を睨んでの拘束でした。すなわち薄板裏面の状況を一致させるために1.1項ではリベット後半120度の拘束としました。

尚応力表示をσxからフォン・ミーゼス応力に変更したものを以下に示します。
薄板とリベットの接触部の応力は405MPaに達しており、挫滅が発生し始めるレベルと推定されます。但しFEMでは角張った接触部には大きな応力が立ちやすいので、これにより直ちに問題となる訳ではないと考えます。

2.1 疲労計算
以下にシンプルな疲労計算を示します。
アルミ2024-T4材の疲労曲線は以下の条件で約1x106cycle程度(B改訂2025.4.1)と参考文献[1]から読み取れます。
・σ=36ksi(250MPa):1.2項及び1.3項のFreeCADによる計算値
・Kt=1.6 :ノッチ係数。この程度と仮定(1.6 or 2.4 or 3.4から選択)
・stress ratio=0.06:現状の想定は0のため近い値を選定
以上より疲労が始まる時間は以下となります。
T = 1×106 ÷ 14Hz = 20時間(B改訂2025.4.1)
この値にスキャッター・ファクター※1を4とすると推奨される寿命は以下となります。
寿命 = 20 ÷ 4 = 5時間(B改訂2025.4.1)
得られた寿命は意外に短いものとなりました。
尚一般的に応力解析ではフォン・ミーゼス応力や主応力を扱う事が多いと思いますが、理論値との比較の関係からここではσxで検討しました。
また今回はリベットを1列に打鋲しましたが、2列(千鳥)に打つことで強度不足を補うことがよく行われているようです。
※1スキャッター・ファクター:
疲労計算に用いる時間軸の設計マージンで、一部の産業ではだいたい3~4が使われているようです。
3 応力集中の考察
応力集中の様子を下記のような簡単なサンプル・モデルで確認してみます。1項、2項とはモデル形状の違う単純な板の引っ張りでの応力集中を計算してみました。
・入力負荷(左端面) 85Mpa
・右端面拘束
結果は以下で円の中央縁部で大体250MPa位で入力負荷の3倍くらいになっています。
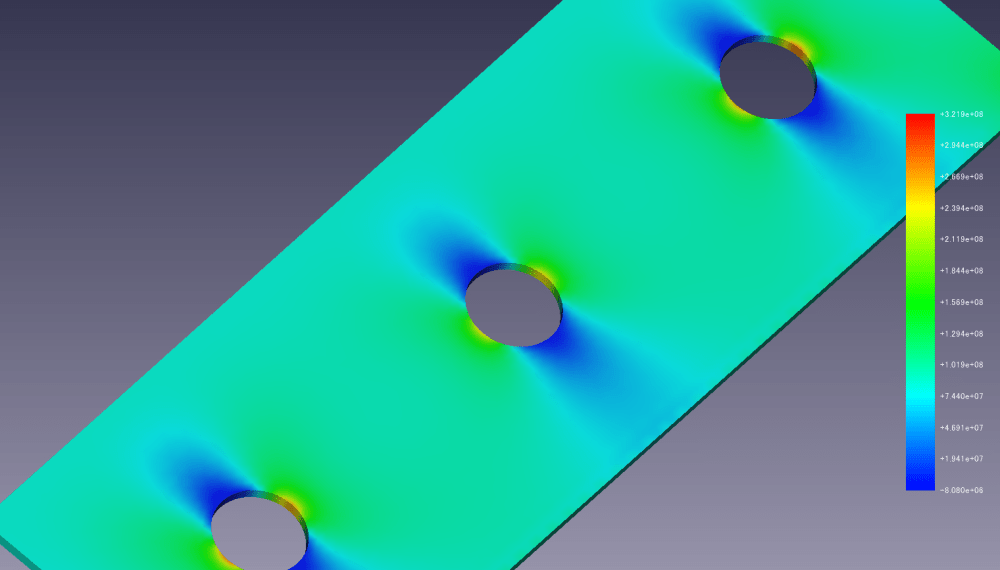
上記計算の応力の流れをParaview※1を用いて可視化してみます。
この流れの様子から分かることは上流側応力は穴によりせき止められ、その分の穴の脇を抜けていきます。そしてその脇に抜ける量が円の直径に対して約1/3位に見て取れます。このため印加した応力85MPaの約3倍の応力が円の縁に加わっていると考えられます。
※1ParaView:データ可視化用の米国製オープンソース

参考文献
[1]MIL-HDBK-5J 31 January 2003 METALLIC MATERIALS AND ELEMENTS FOR AEROSPACE VEHICLE STRUCTURES
改訂記録
A改訂 2025.3.22:円柱外板位置を後方から前方に移動
B改訂 2025.4.1:疲労曲線から読み取る疲労サイクルの変更。これに伴い寿命の変更。
