強度解析にて必要となる以下の項目をFreeCADを用いて確認してみます。
・モールの応力円を用いた主応力
・曲げとねじりの組合せ応力
1.応力の定義確認
検討すべき応力の確認を行います。
強度解析にて微小要素にて定義される応力は以下の9個となります。
・x面に関し:σxx x方向への垂直応力、σxy y方向へのせん断力、σxz z方向へのせん断力
・y面に関し:σyx x方向へのせん断力、σyy y方向への垂直応力、σyz z方向へのせん断力
・z面に関し:σzx x方向へのせん断力、σzy y方向へのせん断力、σzz z方向への垂直応力
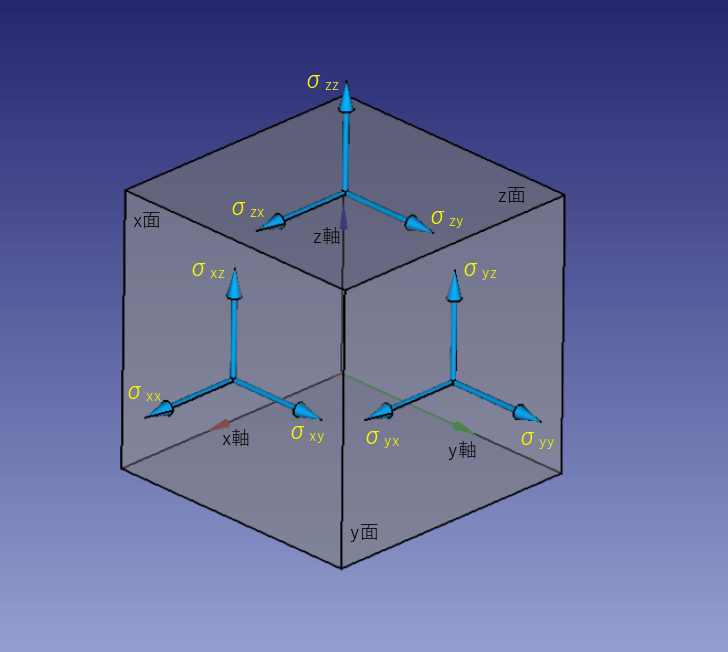
上図は表面を示しましたが、裏面にはこれらを打ち消すように9個の応力が働きます。 一方この状況をz面の上方から見た状態が以下です。
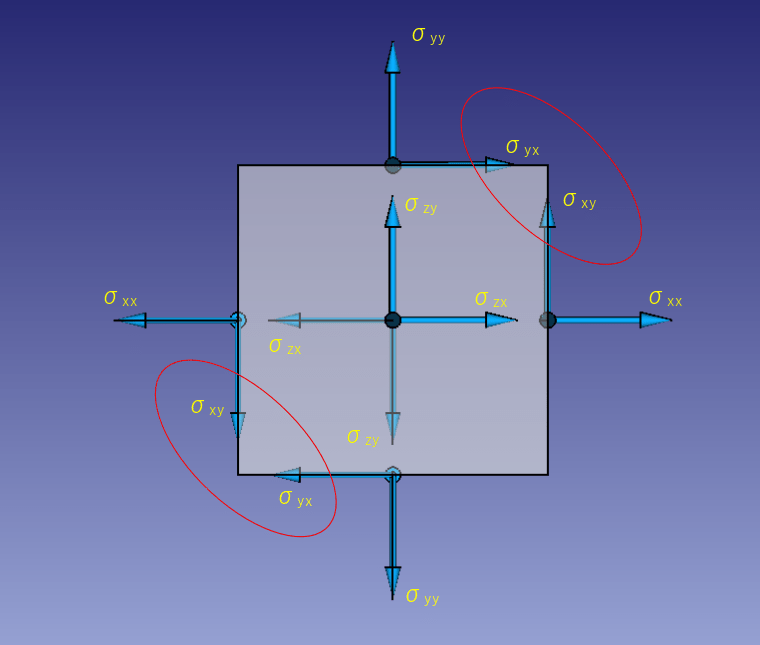
微小要素は静的に釣り合っている状態を考えます。このため上図の微小要素がz軸周りに回転しないための条件として
・σxy=σyx
同様にして
・x方向に関し:σyz=σzy
・y方向に関し:σxz=σzx
以上より静的に釣り合っている微小要素における独立した応力(応力テンソル)は以下の6つとなります。
σxx、σyy、σzz、σxy(τxy)、σyz(τyz)、σzx(τzx)
これ以降、三角形の斜辺における応力を議論しますが、FreeCADにおける応力はあくまで上述6個となります(物体の斜面でも上述6応力となり、斜面に沿った応力ではない点を注意する必要があります)。
2.モールの応力円を用いた主応力
2.1 三角柱の表面応力
主応力を確認する前にまずσxxとσyyの様子をFreeCAD(下図)で確認します。
〇解析条件
・直角二等辺三角形の三角柱:二等辺の一辺10mm、高さ10mm
・直角三角形の二等辺の面に100kPa印加
・斜辺の面を固定
・メッシュ:Netgen 最大サイズ1mm、非常に粗い
・材質:一般鉄

〇解析結果 フォンミーゼス応力(後述)
FreeCADでは変形を考慮するため、斜面の縁に応力が集中しています。印加応力が100kPaに対し、縁では200kPaに達しているようです。しかしそれはあくまで局部的であり、全般的には100kPaとなっています。

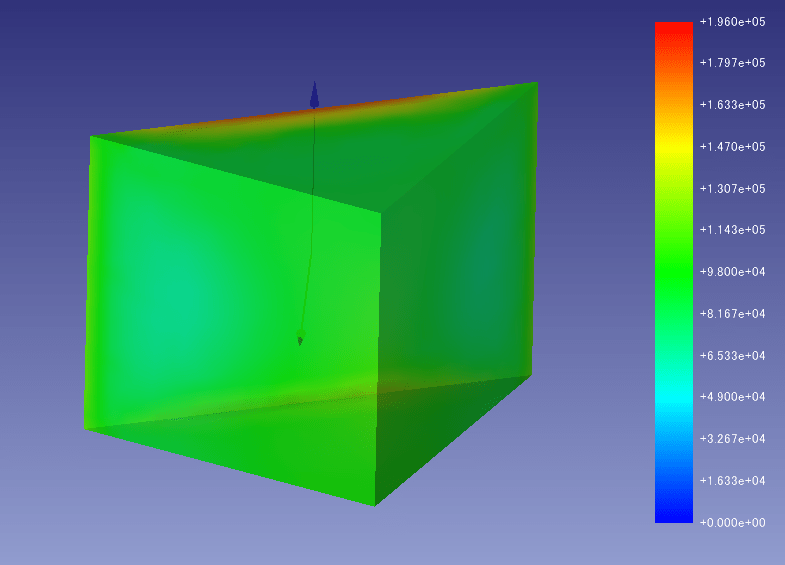
〇解析結果 σyy(三角柱を真ん中で切り落として表示)
斜辺の面と二等辺の面が100kPaの応力でつながっていることが見て取れます。
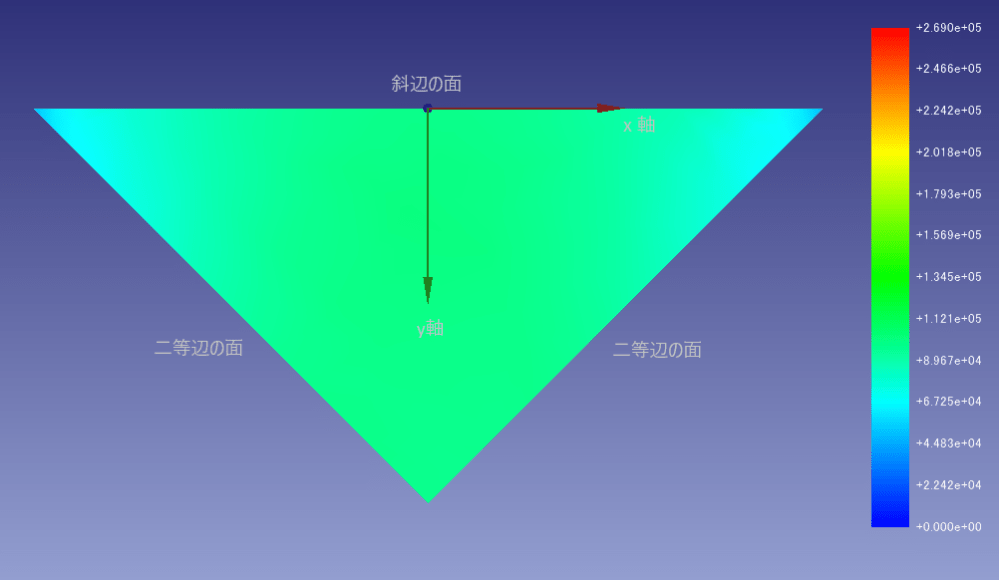
〇解析結果 σxx
斜辺の面にσxxは発生していませんが、二等辺の面には100kPaの応力が発生しています。

斜辺の面にはσxxとσyyとして100kPaの応力が発生しているため、合力としては面に√2倍の応力が発生しそうに感じますが、面積も√2倍となるため、結果斜辺の面に垂直な応力は100kPaとなります。結局、三角柱に発生する表面に垂直な応力はすべて100kPaとなりました。
2.2 三角柱の表面応力その2
2.1項で計算した三角柱を20°位傾けることで敢えてせん断力を発生させてみます。
〇解析条件
・直角三角形の二等辺の面に100kPa印加
・斜辺の面を固定
・メッシュ:Netgen 最大サイズ1mm、非常に粗い
・Z軸まわりに20°回転。
〇解析結果 フォンミーゼス応力(後述)
計算結果は当然ながら2.1項と同じ結果となります(Z軸回りに20°回転しただけです)。
〇解析結果
σyy、σxx 2.1項とは変わり、座標系が傾いた分、応力に偏りが見られます。
2.1項ではほとんど発生していなかったσxyが数値を上げています。



「モールの応力円」は検査面次第で応力が変わるということを示していると言えます。
2.1項と2.2項の計算結果はまさしくその様子を示しています。
ここでは「モールの応力円」の公式を用いて、上述2.2項の結果から2.1項の計算結果を求めてみます
FreeCADの計算結果をParaviewに移行して斜辺中央辺りの数値を読み取ってみます。
(FreeCADでは任意の点の応力を読み取れないようです。)
σyy=98055Pa
σxx=50073Pa
σxy=-19082Pa

ここで以下のモールの応力円の公式を用いて主応力を計算してみます。
σ1,σ2 = 1/2*(σxx+σyy) ± 1/2*√((σxx-σyy)2+4*σxy2)
∴σ1,σ2 = 1/2*(98055+50073) ± 1/2*√((98055-50073)2+4*190822) = 105kPa、43kPa
また別のモールの応力円の公式より傾き2θを計算してみます。
tan2θ=2σxy/(σxx-σyy)
∴tan2θ=2*19082/(98055-50073) θ=19.2°
結果、2.1項とほぼ同じ応力105kPaの計算値が得られ、また本項で設定した傾き20°とほぼ同じ19°が得られました。 参考までに下図にparaviewで可視化した変位ベクトル流線(変位ベクトルの方向に沿った線)を示します。この計算では主応力が斜辺の辺に垂直に伸びることは自明なので、これよりparaviewの変位ベクトル流線と主応力の方向は一致すると考えて良さそうです。

2.3 モールの応力円
前項2.1項と2.2項の内容がモールの応力円の様子(参考文献[1]9.2項)を示しています。
具体的には三角柱の斜辺の面がy軸と直行するモデル(2.1項)では応力はσyyしか発生しないのに対し、y軸と20°傾きを持つモデル(2.2項)では応力σyy、σxx、σxyが発生しています。つまり座標軸が変わることで内部応力(応力テンソル)が変化する様子を確認出来たことになります。
モールの応力円を下図に示します。 ある点での応力(σxx,σyy,σxy)から作成された円上(下図)に存在する点が主応力面からθ°傾けた検査面にて計測される応力(σxx,σyy,σxy)を示します。例えばσ軸との交点は大きい方がσ1(最大主応力:x方向)、小さい方がσ2(最小主応力:y方向)を示しており、この場合はせん断応力σxy=0となります。

今一度2.1項計算値と2.2項計算値を用いてモールの応力円(上図)を確認してみます。
・2.1項
σxx=0Pa、σyy=100kPa、σxy=0Pa
・2.2項(2.1項をθ=20°回転)
モールの応力円公式より
σyy=50kPa*(1+cos2θ)=88.3kPa vs σyy=98kPa(FreeCAD)
σxx=50kPa*(1-cos2θ)=11.7kPa vs σxx=50kPa(FreeCAD)
σxy=50kPa*sin2θ=32.1kPa(符号無視) vs σxy=-19kPa(FreeCAD)
モールの応力円公式による理論値とFreeCAD計算値とはかなりずれています。モールの応力円で表現すると半径30.6kPa、中心74kPaに変化しています。
イメージとしてはσyyの応力100kPaがσxxに43kPa移行した感じです。これはy軸変形がx軸方向に逃げたことを示していると考えられます。そこでFEM計算のポアソン比を0にしてみます(上記計算では0.29でした)。
結果は以下で、上記理論値とかなり近い値になりました。それでも違いがあるのは固定面でも荷重分布にムラ(下図フォンミーゼス応力)ためと推察します。
σyy=88.3kPa(公式) vs σyy=117kPa(FreeCADポアソン比0)
σxx=11.7kPa(公式) vs σxx=15kPa(FreeCADポアソン比0)
σxy=32.1kPa(公式) vs σxy=-42kPa(FreeCADポアソン比0)
逆に考えますと机上計算では扱うことの難しいポアソン比の影響をFreeCADは取り扱えることが伺えます。

3.1 曲げとねじりの組合せ応力
2項までの議論は主応力が検査面次第では垂直応力とせん断力に分解されることを確認してきました。
本項ではその逆で曲げとねじりにより発生する垂直応力とせん断力の組合せをモールの応力円から主応力にまとめることを確認します。
以下のような曲げとねじりの組合せを考えます。
・直径20mm、高さ100mmのアルミ棒
・10N×20mm(=0.2Nm)の曲げモーメント(端面に局所的に10Nを上下に印加)
・5N×4×10mm(=0.2Nm)のねじりモーメント(端面に局所的に5Nを4個所に印加)
・メッシュ:Netgen 最大サイズ2mm、非常に粗い
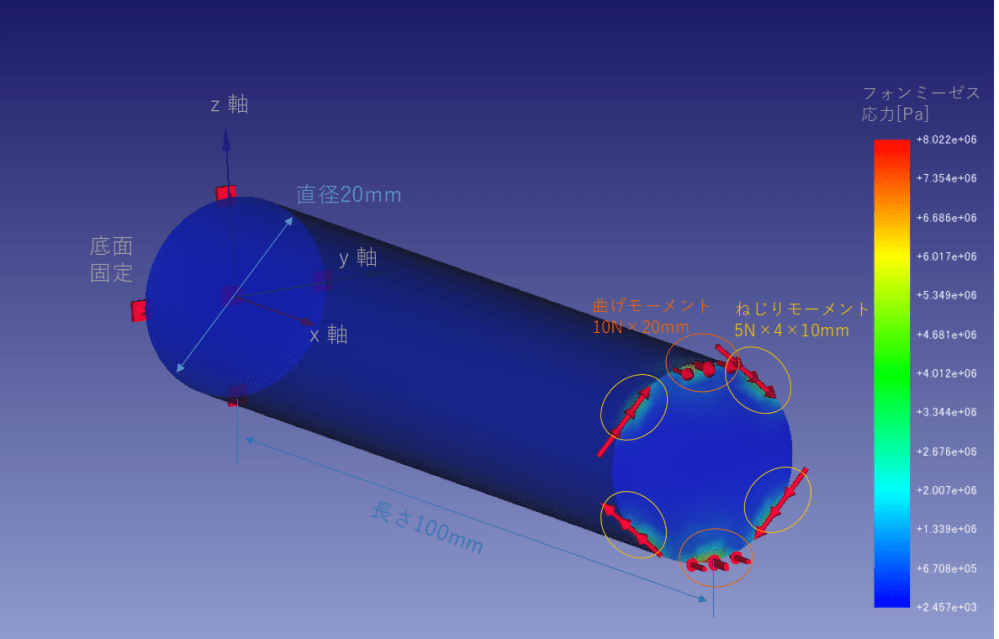
机上計算(基本的な材料力学公式)より発生する応力は以下となります。
・曲げモーメントによる垂直応力σxx
σxx=M*(d/2)/I=0.2*0.01/(π*0.024/64) = 255[kPa]
M=0.2Nm:印加曲げモーメント
d=20mm:棒の直径
I=πr4/4=πd4/64:棒の断面2次モーメント
・ねじりモーメントによるせん断応力σxy(τxy)
σxy=T*(d/2)/J=0.2*0.01/(π*0.024/32) = 127[kPa]
T=0.2Nm:印加ねじりモーメント
d=20mm:棒の直径
I=πr4/2=πd4/32:棒の断面2次極モーメント
モールの応力円より
σ1,σ2 = 1/2*(σxx+σyy) ± 1/2*√((σxx-σyy)2+4*σxy2)
∴σ1,σ2 = 1/2*(2.55+0) ± 1/2*√((2.55-0)2+4*1.272) = 307kPa、-52.5ekPa (σyy=0とした)
また以下の公式より傾き2θを計算してみます。
tan2θ = 2σxy/(σxx-σyy)
∴tan2θ = 2*1.27/(2.55-0) θ=22.5°
一方FreeCADの計算結果を以下に示します。

FreeCAD計算より
σxx=235k[Pa] <=机上計算値 255k[Pa]
σxy=118k[Pa] <=机上計算値 127k[Pa]
σmajor=284k[Pa] <=机上計算値 307k[Pa]
σminor=-48.9k[Pa] <=机上計算値 -52.5k[Pa]
これらは机上計算とほぼ一致しています。
(若干のずれは2.3項で示したポアソン比の影響と推定されます。)
続いて検査面の傾きθについて確認してみます。
2.2項よりparaviewによる変位ベクトルの流線が主応力の方向に一致しそうなことを確認しています。そこで今回の組み合わせ応力の計算結果をparaviewで観察しました。 下図のようにねじりモーメントによる変位円が曲げモーメントにより傾ている様子が見て取れます。
下図のようにねじりモーメントによる変位円が曲げモーメントにより傾ている様子が見て取れます。その角度は図からの読み取りで約24°(2θ=48°)となり、机上計算22.5°とおよそ一致します。

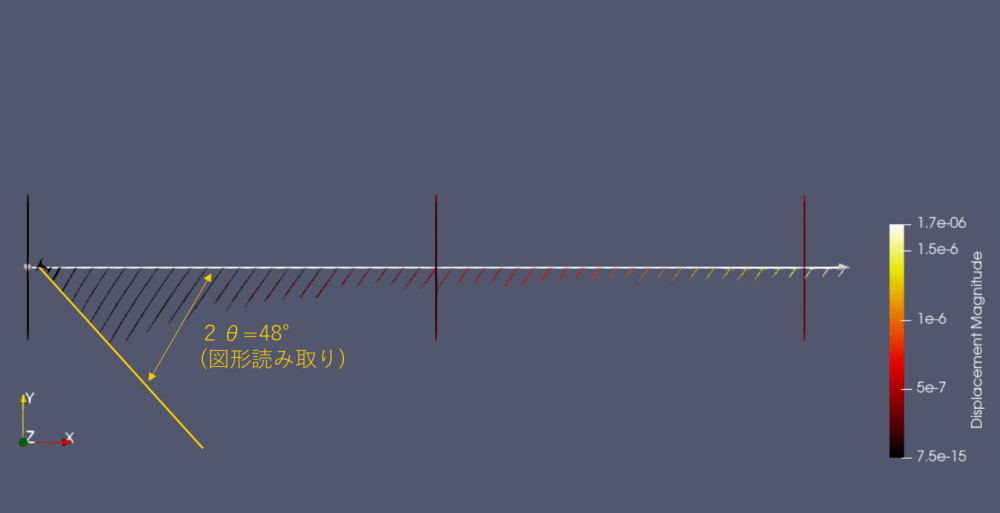
これはねじりモーメントにより発生した応力が曲げモーメントによって傾くことを示しています。
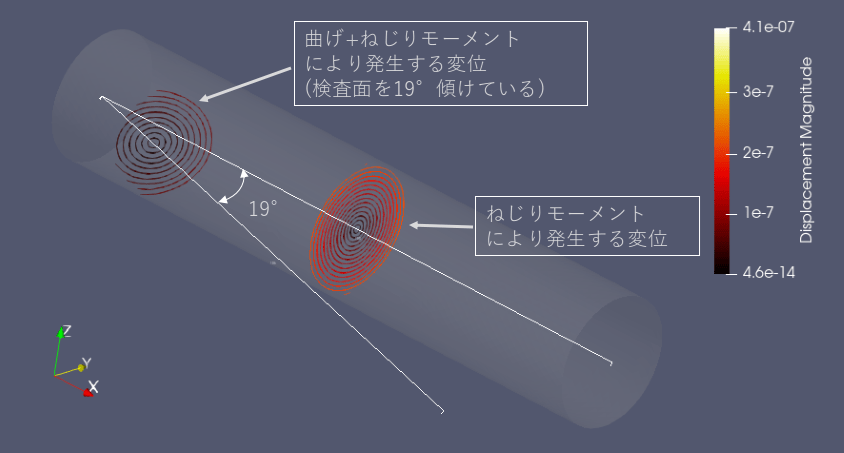
そこでpaviewの検査面を傾けて実際応力面が傾てい要るかを確認しました。
下図に示す通り確かに変形面が傾ています。但しここでは19°位の傾きで、また少し違った数字となっています(実際の応力は理論通りにはいかないようです)。
それにしてもねじりモーメントに曲げモーメントが加わると思いもよらない方向に応力面が傾くようです。
「補足」
構造解析において今まで検討した主応力とは別にフォンミーゼス応力というものがあります。
こちらは延性材料の降伏点の評価基準によく用いられ、CAE解析ソフトウエアの出力に多くの場合存在します。
延性材料ということで金属製品を設計する場合はこちらが有望となります。
式は以下となります(参考文献[2]2.2項)。
応力テンソルはベクトル表示ですが、フォンミーゼス応力はスカラーとなります。
σeq = √{ (σxx-σyy)2/2+(σyy-σxx)2/2+(σzz-σxx)2/2+3(σxy2+σyz2+σzx2)}
または
σeq = √{ (σ1-σ2)2/2+(σ2-σ3)2/2+(σ3-σ1)2/2} σ1、σ2、σ3:主応力
仮に主応力がσ1以外0の場合、フォンミーゼス応力σeqは主応力σ1と一致します。
4.三次元での主応力
4.1 主応力は応力テンソルの対角化(固有値)
モールの応力円を別の観点から復習します。
モールの応力円を作成するのは、微小三角形での垂直応力とせん断力の釣り合いから求めています。
この点を単なる応力テンソルの対角化として考えてみます。
前項の三角柱を20°回転したときの応テンソルはモールの応力円より以下となります。
σ
=
| σxx | σxy |
| σyx | σyy |
=
| 11.7 | 32.1 |
| 32.1 | 88.3 |
σxx = 50kPa*(1-cos2θ) = 11.7kPa
σyy = 50kPa*(1+cos2θ) = 88.3kPa
σxy = 50kPa*sin2θ = 32.1kPa
上記応力テンソルσの固有値及び固有ベクトルを計算(対角化)してみます。
ここでは手を抜いてScilabのeingenコマンドで求めてしまいます。
(細かい計算はScilabにまかせてしまいます。)
[V,D]=spec(σ);
結果、 (単位kPa)
D
=
| 0.027 | 0 |
| 0 | 99.97 |
V
=
| -0.9398 | 0.3417 |
| 0.3417 | 0.9398 |
固有値Dを見るとおよそ100kPaになっています。
また傾きも固有ベクトルVの傾きを計算すると20°となっています。
傾きθ = tan-1(0.3147/0.9398) = 19.98
以上、主応力を求める行為は応力テンソルの固有値を求めることと同じということが推定されます。固有値を求める行為は解析空間で回転を行うことと同じとなりますが、主応力を求める際もせん断力を分解して垂直応力と同等に扱っています。よって本質的には同じことのようです。
次項では3次元での応力テンソルを扱ってみます。
4.2 三次元での主応力
3次元応力テンソルにおける主応力を計算してみます。
ここでは2.1項で計算した三角柱をFreeCADを用いてz軸に20°、x軸に30°回転してみます。
実施した結果が以下です。
〇解析条件
・直角三角形の二等辺の面に100kPa印加
・斜辺の面を固定
・メッシュ:Netgen 最大サイズ1mm、非常に粗い
・z軸まわりに20°回転、のちにx軸に30°回転。
・回転を明確にするため、ポアソン比は「0」。
・上図:FreeCAD フォンミーゼス応力、下図:Paraview フォンミーゼス応力

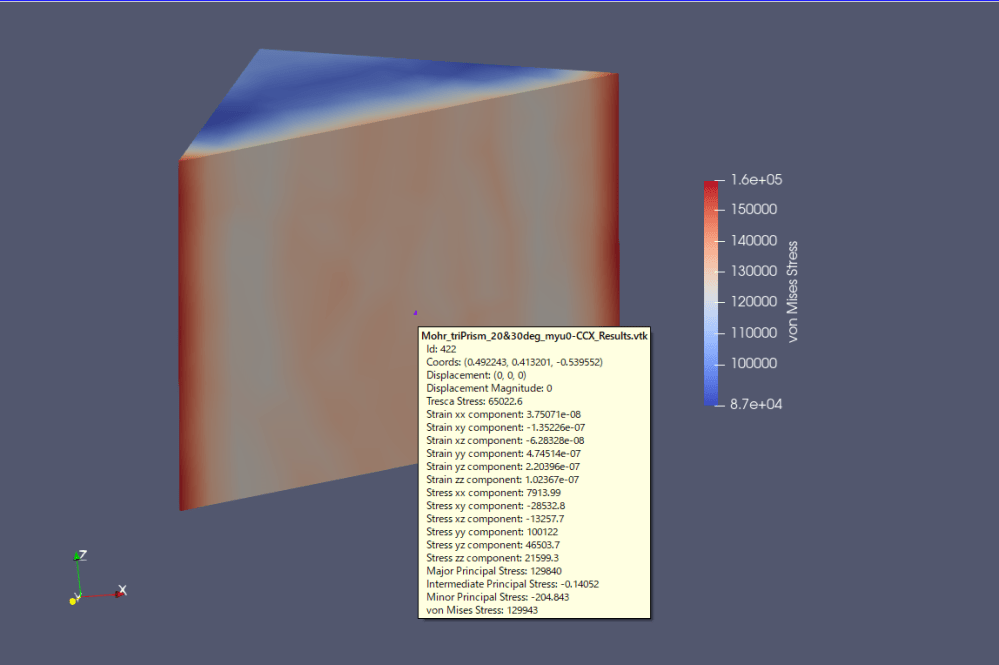
ここで4.1項と同じように応力テンソルの対角化を考えて見ます。
上図FreeCAD計算結果から読み取ると
σ
=
| σxx | σxy | σxz |
| σyx | σyy | σyz |
| σzx | σzy | σzz |
=
| 7.91 | -28.5 | -13.3 |
| -28.5 | 100 | 46.5 |
| -13.3 | 46.5 | 21.6 |
この応力テンソルσの対角化を以下のScilabコマンドで実施します。
[V,D]=spec(σ);
結果、
D
=
| -0.219 | 0 | 0 |
| 0 | -0.009 | 0 |
| 0 | 0 | 129.7 |
V
=
| 0.946 | 0.207 | -0.250 |
| 0.131 | 0.460 | 0.878 |
| 0.297 | -0.863 | 0.408 |
固有値Dを見ると、主応力として129.7kPaともともとの100kPaから増えてしまっています。
しかしこれは2.3項と同様に三角柱固定面に応力のむら(フォンミーゼス応力129.9kPa)が発生しているためと考えられます。この点を鑑みれば、対角化で十分主応力を抽出出来たと考えられます。
実際FreeCADの示している主応力ベクトルを計算結果(上図)から読み取ると以下で、Scilab計算と十分一致します。
[σ1、σ2、σ3] = [ 129.8、-0.000141、-0.205]
またy軸方向単位ベクトルをz軸に20°、x軸に30°回転した場合のベクトルは以下。
rotation [ 0; 1; 0] = [-0.342; 0.814; 0.47]
最大主応力σ1に対応する固有ベクトルV(Scilab計算値)は以下である程度の一致が見られます。
Vσ1 = [-0.25; 0.878; 0.408]
(x成分に違いが大きいん点は変位ベクトル流線の様子を見ると固定面から若干放射上に広がっていることが影響していると考えます。)
以上より主応力の計算は応力テンソルの対角化と同じということが3次元でもおおよそ確認出来ました。
アプローチを変えて出発点であるσyy=100kPaをz軸に20°、x軸に30°回転してみます。
σ
=
| σxx | σxy | σxz |
| σyx | σyy | σyz |
| σzx | σzy | σzz |
=
| 0 | 0 | 0 |
| 0 | 100 | 0 |
| 0 | 0 | 0 |
Rotz20
=
| cos20 | -sin20 | 0 |
| sin20 | cos20 | 0 |
| 0 | 0 | 1 |
Rotx30
=
| 1 | 0 | 0 |
| 0 | cos30 | -sin30 |
| 0 | sin30 | cos30 |
z軸に20°回転し、その後x軸に30°回転します。
σ’ = Rotx30×Rotz20×σ×Rotz20T×Rotx30T
=
| 11.7 | -27.8 | -16.1 |
| -27.8 | 66.2 | 38.2 |
| -16.1 | 38.2 | 22.1 |
この値はFreeCADの計算値とほぼ一致しています(σyyだけは小さいですが)
σFreeCAD =
| σxx | σxy | σxz |
| σyx | σyy | σyz |
| σzx | σzy | σzz |
=
| 7.91 | -28.5 | -13.3 |
| -28.5 | 100 | 46.5 |
| -13.3 | 46.5 | 21.3 |
この点から応力テンソルは主応力の回転であると言えますし、それが故に対角化することが主応力を計算することにつながると考えます。
「補足」
上述応力テンソルの回転では対象テンソルを回転の行列で挟んでいます。
σ’ = Rot×σ×RotT
この点を補足します。
両辺にRot×Vを足します。
σ’×Rot×V = Rot×σ×RotT×Rot×V
= Rot×σ×V
この式の右辺は応力テンソルに任意のベクトルVをかけた後に回転(Rot)することを意味し、左辺は任意のベクトルVを回転(Rot)した後に回転済応力テンソルをかけています。
意味としてはある空間の物理量(応力)はその対象面(任意ベクトルV)を回転してから応力テンソルにかけても(左辺) 、応力テンソルをかけてから回転(右辺)しても同じ値となるという当たり前のことを示しています。
参考文献
[1]これならわかる図解でやさしい入門材料力学 有村隆著 技術評論社
[2]製品開発のための疲労破壊事故の解析と強度対策 鯉渕興二・小久保邦雄・初田俊雄・坂田光児 著 日刊工業新聞社
