「テーマ」

・レーシングカーにおけるフラットボトム・フロアによるダウンフォースの検討

「方針」

　OpenFoamのpisoFoam(RASモデル)によりフロア・ダウンフォースを計算する。

　尚円柱周りの流体解析detail1よりpisoFoamでは乱流の扱いに注意する必要があり、実験値のある亜臨界領域(レイノルズ数2*10⁵以下)が安心な領域ということを確認しました。一方レーシングカーにおけるレイノルズ数は超臨界(2*10⁶)以上の場合が主な設計領域と考えられます。これ以降は実験値との比較が出来ないため、あくまで参考となりますがレーシングカーの領域(超臨界領域)を計算してみます。

---

１．OpenFoamによるフラットボトム・フロアの流体解析

１．１　レーシングカーの形状設定

　レーシングカーと言えばF-1が最も興味の引く領域ではありますが、形状が複雑すぎて今回の試算には適していません。そこで今回はスポーツプロトタイプカーであるGroupCカーをイメージしてみます。有名どころではポルシェ956(下写真)、JAGUAR XJR-14やMERCEDES-BENZ C291といったものをイメージし、簡略化した以下の２つの形を考えていきます(あまりにも貧弱な簡略化は当事業所パソコン性能のためです。ご容赦下さい)。

© ERIC SALARD (Paris, France), via Wikimedia Commons  

Licensed under CC BY-SA 2.0  

https://creativecommons.org/licenses/by-sa/2.0/

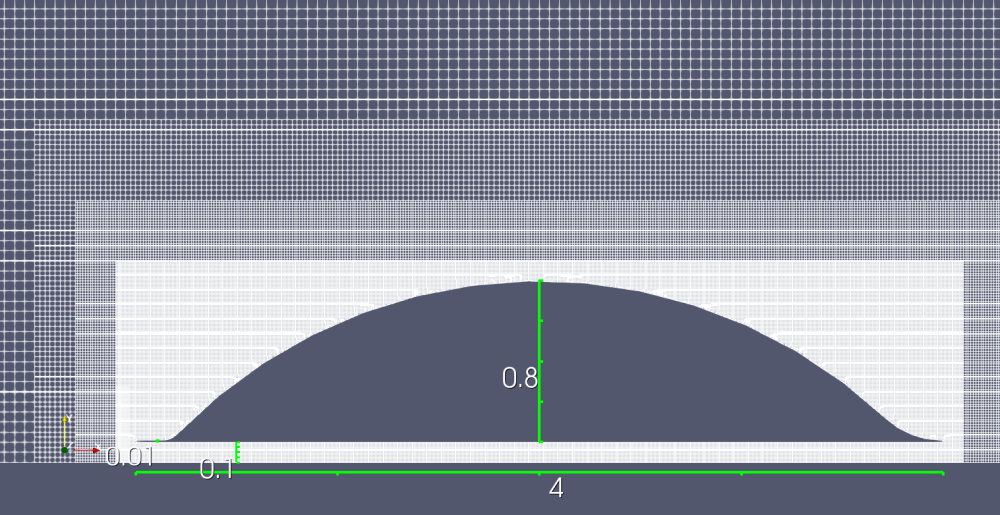
〇Type-1　フラットボトム(デヒューザなし)

・解析空間17ｍ(長さ)ｘ2.5ｍ(高さ)の細長空間(2D)

・車体全長4ｍｘ全高80cm(2D)

・床下地上高　10cm

・前方しきり板厚1cm(多くのレーシングカーのフロントに装着されている平板)

・周囲風速：50 m/s(時速180km)

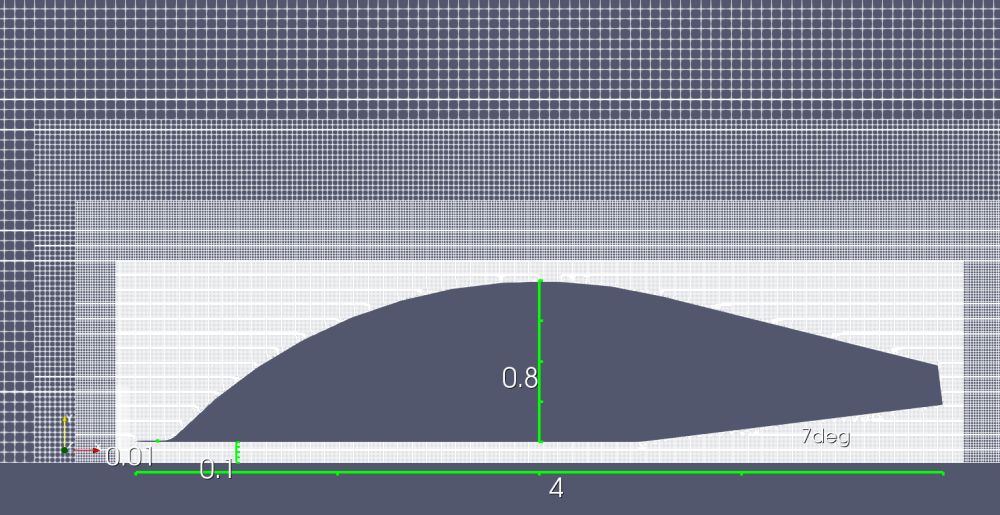
〇Type-2　フラットボトム(デヒューザ装備)

・７度の角度をもったデヒューザを装備(その他はType-1と同じ)

---

１．２　レイノルズ数確認

　代表点のレイノルズ数を計算しておきます。

・先端平板部

　Re=50[m/s]*0.01[m]/ 2e-5 = 2.5*10⁴

・車体(ボディー)

　Re=50[m/s]*0.8[m]/ 2e-5 = 2*10⁶

　先端部は亜臨界(Re<2*10⁵)の領域であり安心して模擬出来そうですが、ボディー部は超臨界(RE>2*10⁶)の領域にいます。よってボディー部の挙動は詳しく見る必要があります。

---

１．３　OpenFoam設定。

　CFD計算条件を以下に示します。

・メッシュ：17(長さ) x 2.5(高さ) x0.04(幅)mを340x50x1の合計17000マスに分割(２次元)。

　車体周りを更に3段階で8倍細密化(1メッシュサイズは6.25mmｘ6.25mm)。

・積分幅：Type-1=2.5e-5秒(5e-5では計算発散)、Type-2=5e-5秒

・クーラン数：Type-1=0.2(=50[m/s]*2.5e-5[s]/0.00625[m])、Type-2=0.4　

・周囲速度50m/s、上面slip条件、下面は50m/s。

・圧力：出口をゲージ圧0で固定。

・空気動粘性：2.0e-5 m²/s

・解析ソルバーはpisoFoam(非圧縮・非定常乱流解析ソルバー)

・乱流モデルはRAS(レイノルズ平均に基づく乱流モデル)でkEpsilonモデル(標準ｋ-εモデル)

・乱流散逸率epsilon、乱流エネルギーk及び乱流比散逸率omegaの初期値は参考文献[1]4.5.5章の計算値の約1/5を設定。

・乱流動粘性係数nutの初期値は0とし、nuTildaは無視(使われていない。たぶんomegaも使われていない)。

 上記以外のパラメータは以下のOpenFoamチュートリアルの物をそのまま使用。

    tutorials\incompressible\pisoFoam\RAS\cavity

---

１．４　Openfoam計算結果

　上述条件で計算した結果を以下に示します。

〇Type-1：解析空間計算時間　0.5秒　/　壁関数Y+　Ave 333(妥当な範囲)

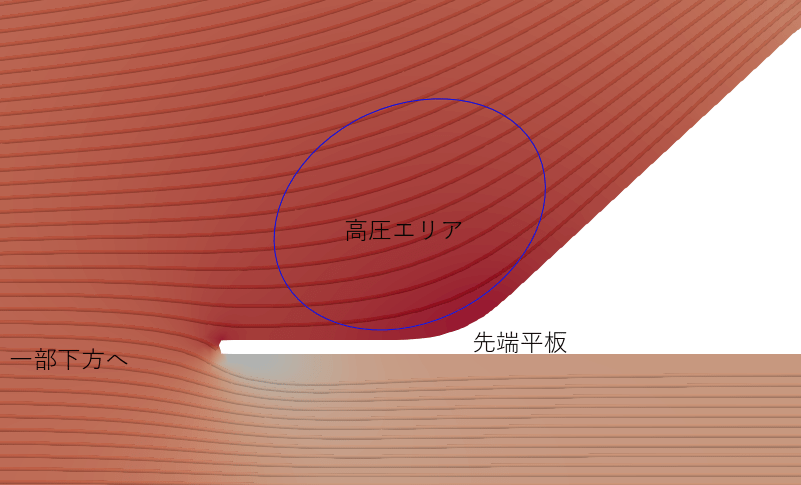
・床下の速度は若干増速(周囲速度50[m/s:]に対して56[m/s]位)

（これは前方からの気流の一部が先端の平板上面にて発生した高圧エリアを下側に避けた為と考えられます。）

・車体上部では速度が100[m/s]まで増速

（相当な増速のため車体頭頂部を超えて早々に気流が剥がれだしています。）

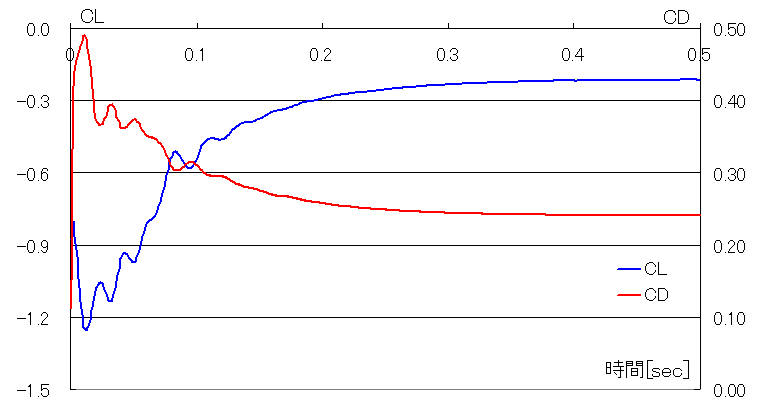
・揚力係数Cl=+0.69(浮揚する方向)、抵抗係数Cd=0.21位に収束

（尚Clの代表面積は上方投影面積、Cdの代表面積は前方投影面積を用いています。）

・後流の脈動が少ない。本計算がちょうど臨界領域の計算になっている可能性がある(詳しくはこちら)。この場合Cl、Cdは実験値から離れている恐れあり。実験値との比較が必要。

（超臨界のCdが臨界値のおよそ2.5倍に増加している円柱実験値(インターネット情報)があります。このため今回の計算値であるCd値もその程度の変動が起こりえます。Clに関しても上面負圧領域が剥離により増加することで相当な変動(浮力増加)が考えられます。)

〇Type-2：解析空間計算時間　0.5秒　/　壁関数Y+　Ave 386(妥当な範囲)

・デヒューザの効果で床下の速度は周囲速度50[m/s]に対して約1.5倍の76[m/s]に増速。

・車体上部では速度が97[m/s]まで増速

（頂上部を超えたあたりから車体形状をなだらかにしたため、気流剥がれは起きていません。）

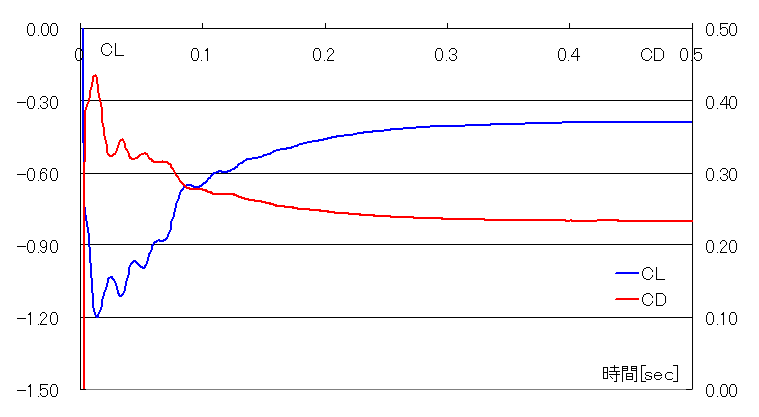
・揚力係数Cl=-0.39(ダウンフォース)、抵抗係数Cd=0.23位に収束

（Type-1に比べてCdがほとんど増えていないのに、Clは一転してダウンフォースに切り替わっています。）

・車体上部、及びデヒューザ部の流れに剥離はなく、安定した性能が維持出来る見込み

　(剥離はしてませんが、境界層検討時kの比較からフロア下はほぼ全域乱流境界層に成長しているようです。)

・Type-1と同様に後流の脈動が少ない。この場合Cdは実験値から離れている恐れがあり、実験値との比較が必要。　

　(Cdは最大2.5倍になる恐れがあり、Clもダウンフォースが増加する可能性があります)。

　デヒューザによって得られたClは-0.39で大きく見えませんが、抵抗がほとんど増えていません。更に床下面積はリアウイングの数倍(3倍位)あるため、実質Clは-1.2の価値があります。

---

１．５　まとめ

　デヒューザーにより僅かな抵抗増加で大きなダウンフォースを得られることを確認出来ました。

一方実際に設計する際には以下を考慮すべきと考えます。

　(レーサーの設計経験がないのに恐縮ですが述べさせて頂きます)

・3次元ではフロア下の低圧領域が外気と圧力差及び速度差(粘性せん断力)のために混ざりだす。

　(1970年代のF-1ではスライド・スカートが装備されていた(ロータス78))

・ダウンフォースを発生させる際、ピッチダウンのモーメントも発生する(リアウイングが必要)。

・走行中は外乱が入り込んでくるので、その都度ダウンフォース及びピッチダウン・モーメントは脈動する。

・路面ギャップ等の外乱でノーズが跳ねた時、空気力によってバク転しないかを静的及び動的に確認する必要あり。

　(動的の意味は跳ね上がり角度を予想することです)。

・ノーズが跳ね上がった状態での空力的横及び方向安定を考慮する必要がある。

　(最後まで安定させるか早々に不安定にするかを考える必要があると思います)。

---

[補足]

　敢えてデヒューザー部に1cmのギャップを付けた場合、ダウンフォースにどの程度悪影響が出るかを見積もってみました。

　・フロアとデヒューザー部の境界に1cmのギャップを設定。

　・デヒューザー出口部面積を維持したデヒューザー傾斜とする。

結果、空力性能は以下のように悪化しました。

　Cl　-0.39　⇒　-0.21

　Cd　0.23　⇒　 0.24

　フロア負圧　-2000Pa　⇒　-1700Pa　

　僅か1cmのギャップでダウンフォースは半減してしまいました。図から見た負圧はそれほど変わっていない(15％減)のに大きな変化に見えます。しかしデヒューザー無しのCl＝+0.69からの比率で考えると(-0.39-0.69)*0.85+0.69=-0.23で妥当と考えられます。

---