「Detail3」変形法による薄板FEM応力解析詳細

１．１　応力計算

　Deail2にて作成した下記Scilabモデルの赤矢印の部分が入力{δ}={ω、ω_x、ω_y}に対応した{F}={F、M_x、M_y}となります。Scilabを用いて計算してみたいと思います。

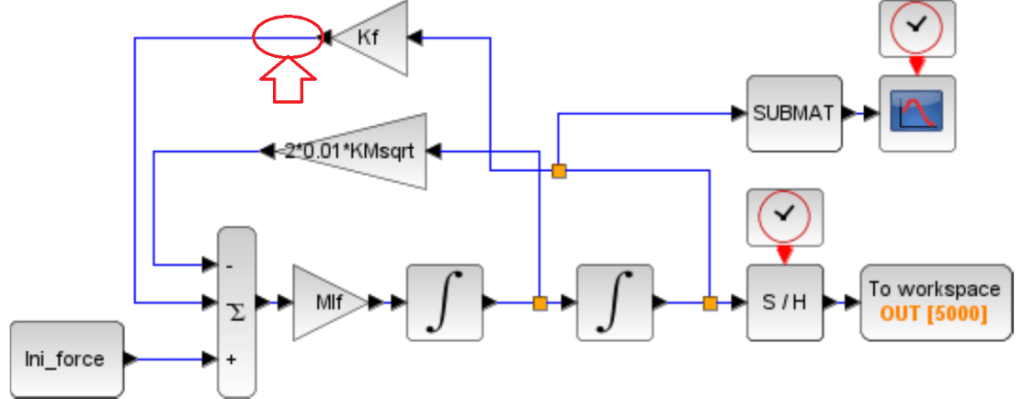
・E：ヤング率 　　　70G[Pa]

・ρ：密度      　　2800[kg/m³]　　　　　　　　

・Ｌ：要素の縦長さ  50[mm](全体で500ｘ500mｍ)　・・・(1)

・ｔ：厚さ　　　　 0.5[mm]

・ν：ポアソン比　　0.3

・Ini_force：150Pa(適当)全面印加

計算結果（変形量）：中央部で15.1mm

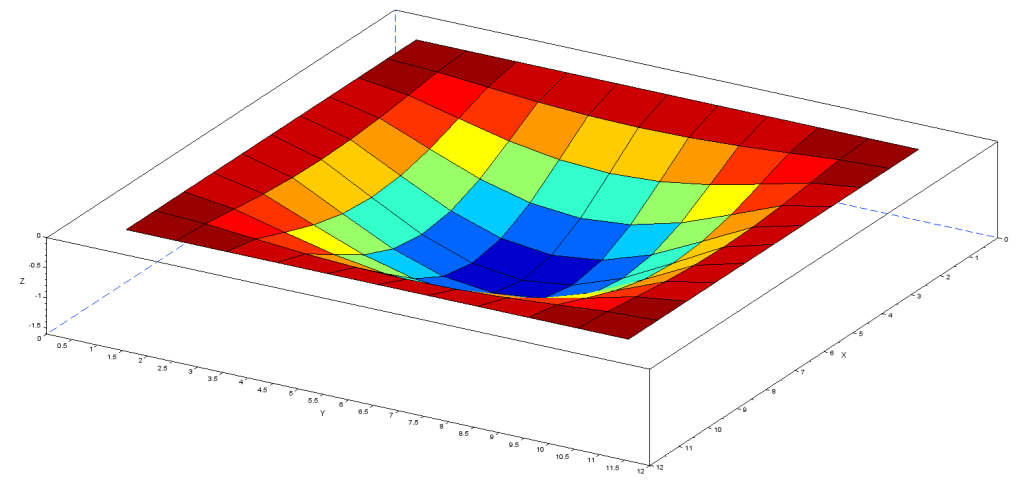
計算結果（曲げモーメントMx）：最大0.75μNm

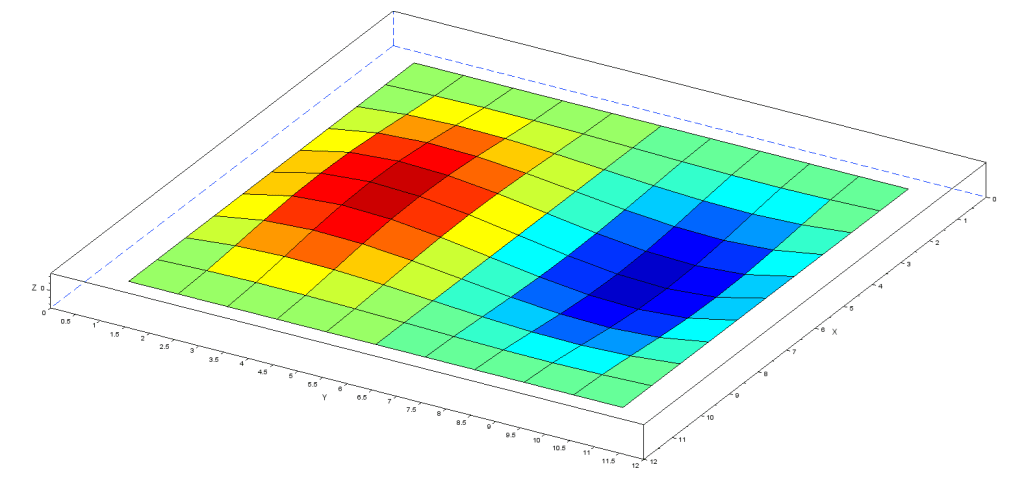
上記計算結果の検証のため理論式による薄板曲げモーメント及び応力（参考文献[1]）を以下に示します。

　ωmax=0.0138 *q * a⁴ / (E*t³)=14.8mm

　M_xmax=0.0513 *q * a² = 1.924Nm(注意：単位長さ辺りの曲げモーメント)　　　・・・(2)

    E：縦弾性係数　70GPa(アルミ)

　q：面圧 150Pa

    a：１辺長さ 0.5m

　t：板厚0.5mm

　変位はScilab計算結果と理論値がほぼ一致するのですが、曲げモーメントM_xは全く一致していません。というよりもScilab計算結果は全面的にほぼ「0」となっています。そもそも本モデルは100個の四角要素を重ね合わせて作っています。このため定常的には隣り合う要素の曲げモーメントが相殺していると考えられます。

　相殺する前の曲げモーメントを計算するにはDetail2において求めた下式まで戻る必要があります。

　　　{M_x,M_y,M_xy}^T =[D]{ε}＝[D] [Q][C]^-1{δ} ・・・(3)

各要素ごとに[D]、[Q]、[C]^-1を用意し、そこに{δ}をかけ合わせることで当該要素内の応力が計算出来ます。各要素の端点は隣の要素と重なりますが、そこは連続していると考えます(著しく不連続の場合は各要素の辺の中点を選ぶことも出来ます)。

　ここでは各要素毎の[D][Q][C]^-1を用意し、そこに各要素に対応した{δ}を掛けあわせ、左上点の{M_x,M_y,M_xy}^Tを求めました。それを全要素に実施することで曲げモーメントを計算しています(最終列および最終行は右上点及び左下点の追加計算で求めています)。

計算した結果を以下に示します(注意：単位長さ辺りの曲げモーメント)。

曲げモーメントMx最大：端部で1.897Nm、凹部で-0.8849Nm。

これは理論値1.924Nmと良く一致しています。

　尚ここでは左上の点を基準に計算しましたが、基準を左下、右上、右下に変えてもほぼ同じ値になることを確認しています(打ち消しあってはいません)。

　以上より今回用意したScilab応力解析の妥当性を示すことが出来たと考えます。

　次に応力に着目します。

　応力が厚みZ方向に線形に分布していると仮定した場合、単位長さ辺りの曲げモーメントと応力の関係は以下となります。

　応力σ＝単位長さ辺りの曲げモーメントMx*6/t²  ・・・(4)

上記計算からは応力σ＝45.5MPa(6.6ksi)となります。

例えばアルミ2024-T42材(米国基準品)の場合、以下の特性となり静的には十分耐えられる状況です。

　Ftu(引っ張り終局応力)=393Mpa(57ksi)

　Fty(引っ張り降伏応力)=234Mpa(34ksi)

　Fsu(せん断終局応力)=234Mpa(34ksi)

FreeCADの解析で薄板を固定しているリベット周りを更に解析することで疲労強度を検討してみようと思います。

---

１．２　曲げモーメント補足

　1.1項で計算した下記値についてもう少し調べてみます。

　　{F}={F_z、M_x、M_y}：Scilabモデル[Kf]の出力値

　上記計算値は全面的にほぼ「0」となっています。それは隣合う要素が打ち消しあうからですが、ここでは打ち消しあいが発生しない四角の縁を計算してみます(Scilabモデルでは四角の縁は境界条件「0」としているため計算していません)。

　最もM_x：曲げモーメントが大きくなる下図の点⑥(要素5と要素6の間)を選んでみます。

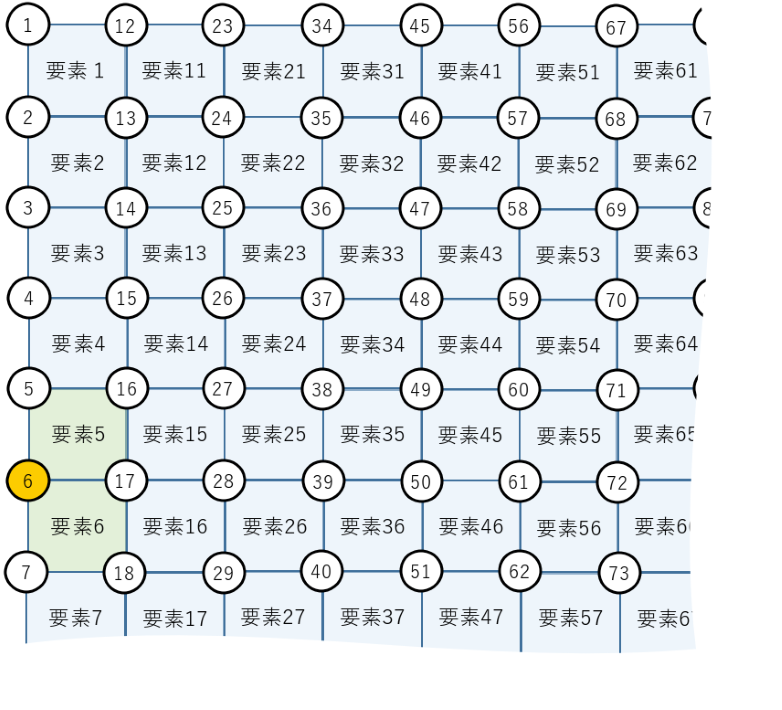
今変数を以下で表現します。

　{F_i}={F_zi、M_xi、M_yi}

　{δ_i}={ω_i、ω_xi、ω_yi}　・・・(12)

要素５、6に関し剛性行列[K₅]、[K_6]を用いることで

{F₅、F₆、F₁₆、F₁₇}=[K₅]{δ₅、δ₆、δ₁₆、δ₁₇}

{F₆、F₇、F₁₇、F₁₈}=[K₆]{δ₆、δ₇、δ₁₇、δ₁₈}　・・・(13)

実際に計算した結果を以下に示します。

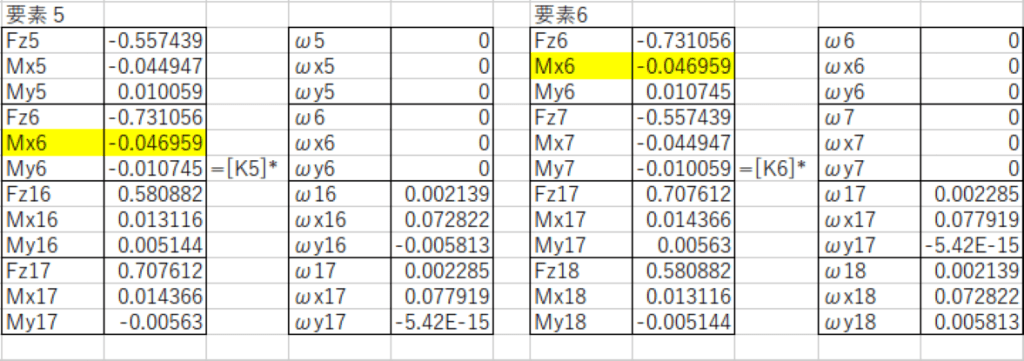
求めるべき点⑥での曲げモーメントM_x6は合計-0.0939Nmとなり、(2)式で計算した1.897Nmと大きく異なります。

　この違いは曲げモーメントM_xの定義の違いによります。(2)式で計算したM_xは対象要素の微小体積dvに対する曲げモーメントを計算しています。このため応力を計算する際は(10)式に従った計算を行います(曲げモーメントは単位長さ辺りの値が計算されています)。

　一方上記Mxは要素５、6(1辺５cmの正方形)を一つの剛体とした場合にx面に作用する曲げモーメントを示しています。このため曲げモーメントは材料力学より以下の式に従います(違いは幅5cm分で単位長さの場合は20倍)。

　σ_x= M_x*(t/2)/I　・・・(14)

　t：板厚み

　I：x面断面2次モーメント　bt³/12

(14)式に従い曲げモーメントを計算してみます。

　σx = 0.0939*(0.0005/2)/(0.05*0.0005³/12) = 45MPa

結果、(10)式の45.5MPaとほぼ一致します。

　本FEMにおける曲げモーメントは扱われる場所により意味合いが違うことが分かりました。

　尚点⑥は四角の縁のため計算出来ましたが、内部の点ではキャンセルしあうため計算値を良く吟味しないといけなくなります。

---