「Detail2」変形法による薄板FEM動的解析詳細

１．１　動的解析モデル作成

Detail1で示しました下記方程式はニュートン方程式の行列版となっています。

このような形の方程式はMatlab(有料数値解析ソフトウェア)やScilab(オープンソース)によって時間変化を解析することが出来ます。

　Scialbの使い方を習得していれば、下図モデルによって簡単に計算が出来ます。

　(尚私の場合、この習得にかなりな時間が必要でした。)

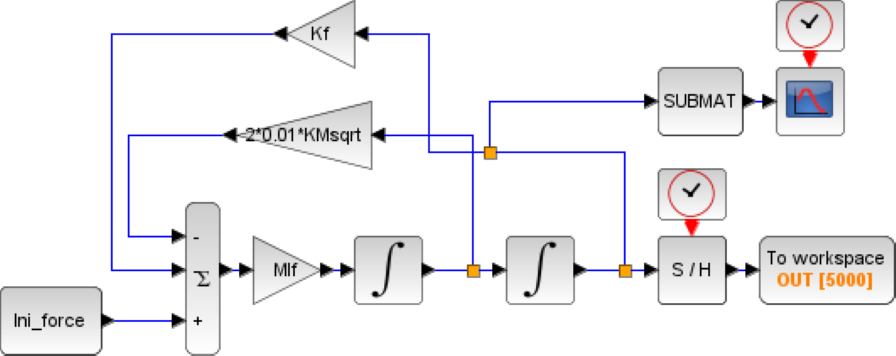
モデルの特徴を羅列してみます。

　・図中の「Kf」が剛性行列[K]、「MIf」が質量行列[M]の逆行列に対応します。

　・「∫」は１回の時間積分を意味します。

　・「Ini-force」により外力が定義出来ます。

　・時計マークのある２つのブロックは出力ポートとなります。

　・モデルの構成は「変位」に剛性行列[Kf]をかけることでばね荷重を計算し、それを質量行列[Mf]で割ることで「加速度」を算出します。加速度を2回積分することで「変位」を算出します。これを一定時間刻みでループさせることでモデル上の時間を変化させて行きます。

　このモデルで注意すべき点として減衰力があります(図中2*0.01*KMsqrtの部分)。一般的には減衰力Fは下記形がよく用いられます。

　F=-[２*ζ*√(KM)]*[dx/dt] ・・・(2)

  ζ：減衰率　積極的減衰デバイスがない場合、目安として1%程度。

　K：剛性

　M：質量

  dx/dt：速度

　今回の薄板運動方程式(1)の変動するωは要素間で擦れる訳でもなく、減衰力をどう定義すべきか悩むところです。現実的には試験を実施し、(2)式に適当な値を入れて合わせこんでいくしかないと考えます。しかし(1)式は行列のため、(2)式を行列で表現する必要があります。

　そこで以降に減衰力の行列表現を検討してみます。

---

１．２　固有ベクトルと基底

　Detail1にてScilabにて計算した固有ベクトルを[P]とし、その際の変位行列を[δ]とした場合、以下の式を満足する[ξ]を仮定します。

　　　{δ} = [P]*{ξ}　　　　　・・・(3)

例えば4次の行列の場合、

ここで変位行列{δ}の時間成分を抽出して以下の式で表現します。

　{δ(t)}={δ}*e^iωt ・・・(5)

(1)式に(4)(5)式を代入すると

　　 [K]{δ} – ω²[M]{δ}

     = [K][P]*[ξ] – ω²[M][P]*[ξ] = 0　・・・(6)

左側より[P]^Tを掛ける。

       [P]^T[K][P]*[ξ] – ω²[P]^T[M][P]*[ξ] = 0　　　・・・(7)

ここで[K]と[M]は対称行列のため、[P]^T[K][P]と[P]^T[M][P]は対角化されます。

対角化された行列を[K’]、[M’]と表すと

       [K’][ξ] – ω²[M’][ξ] = 0　　　・・・(8)

対角化されているため、(8)式は以下のように書き下せます。

　　K₁₁ξ₁ – ω²M₁₁ξ₁ = 0

　　K₂₂ξ₂ – ω²M₂₂ξ₂ = 0　　　　　・・・(9)

　　K₃₃ξ₃ – ω²M₃₃ξ₃ = 0

　　K₄₄ξ₄ – ω²M₄₄ξ₄ = 0

但しK₁₁は[K’]の1行1列要素を示しています。

(9)式の意味するところは{ξ}空間では行間の干渉項がなくなり、独立した運動となることです。

具体的には(4)式において{ξ₁、ξ₂、ξ₃、ξ₄}={1、0、0、0}とおくと

{δ₁、δ₂、δ₃、δ₄}　＝　{P₁₁、P₂₁、P₃₁、P₄₁}　・・・(10)

となり、固有値ベクトルの第1列を示しています。

これは実空間で(10)式の運動をしているものは(9)式の空間ではξ₁が1単位動くだけで、他のξは動かないことを意味しています。

この状況ならば(2)式の減衰力の定義が適用出来ます。

以上より以下のステップで行列を扱った運動方程式の減衰力を定義してみます。尚この試みは当事業所オリジナルの1案であり、対象物の状況により変わるものとなるところはご注意下さい。

(1)　固有ベクトル[P]を用いて[K]と[M]を対角化する([K’][M’])。

(2)　[K’]*[M’]の対角成分の平方根を求める。それを対角行列[√(KＭ’)]と表記しておく。

(3)　上述対角行列を元の{δ}空間に戻すため、左右から[P]^-Ｔ、[P]^-1を掛ける。

(4)　KMsqrt=[P]^-Ｔ[√(KＭ’)][P]^-1としてScilabのモデルに組み込む。

このKMsqrtをScilabモデルに使用します。

---

２．１　動的解析

　1.1項のモデルを用いて実際に10ｘ10マスの薄板動的挙動を解析してみます。

Scilabモデルに使用する変数は以下となります。

・[Kf]：剛性行列　静解析にて計算したもの

・[Mf]：質量行列　静解析にて計算したもの

・[KMsqrt]：1.1項に従い固有ベクトル[P]、[Kf]、[Mf]より計算

・ζ：減衰率。リベット固定構造物における一般的な値として1％を使用

・Ini_force：負荷する外力初期値

・(補足)筆者の好みで積分法はルンゲ-クッタ法、積分幅は100～10μsecで実施しています。

静解析にて使用する変数

・E：ヤング率 　　　70G[Pa]

・ρ：密度      　　2800[kg/m3]　　　　　　　　

・Ｌ：要素の縦長さ  50[mm](全体で500ｘ500mｍ)　・・・(11)

・ｔ：厚さ　　　　　0.5[mm]

・ν：ポアソン比　　0.3

　Ini_forceとして板の自重分を負荷します。その分布は以下としました。

各節点に密度2800kg/m3ｘ厚み0.5ｍｍ分である350gを等分分配します。

但し全重量を400で割り、分配するのは81*4の324です。残り76分は固定節点に負荷されるものとしています。これは1要素の四隅に質量が４等分されるという当事業所の仮定のためです。

F=-0.35*9.807/400*4;

Ini_force=[

F;0;0; F;0;0; F;0;0; F;0;0; F;0;0; F;0;0; F;0;0; F;0;0; F;0;0;

F;0;0; F;0;0; F;0;0; F;0;0; F;0;0; F;0;0; F;0;0; F;0;0; F;0;0;

F;0;0; F;0;0; F;0;0; F;0;0; F;0;0; F;0;0; F;0;0; F;0;0; F;0;0;

F;0;0; F;0;0; F;0;0; F;0;0; F;0;0; F;0;0; F;0;0; F;0;0; F;0;0;

F;0;0; F;0;0; F;0;0; F;0;0; F;0;0; F;0;0; F;0;0; F;0;0; F;0;0;

F;0;0; F;0;0; F;0;0; F;0;0; F;0;0; F;0;0; F;0;0; F;0;0; F;0;0;

F;0;0; F;0;0; F;0;0; F;0;0; F;0;0; F;0;0; F;0;0; F;0;0; F;0;0;

F;0;0; F;0;0; F;0;0; F;0;0; F;0;0; F;0;0; F;0;0; F;0;0; F;0;0;

F;0;0; F;0;0; F;0;0; F;0;0; F;0;0; F;0;0; F;0;0; F;0;0; F;0;0];

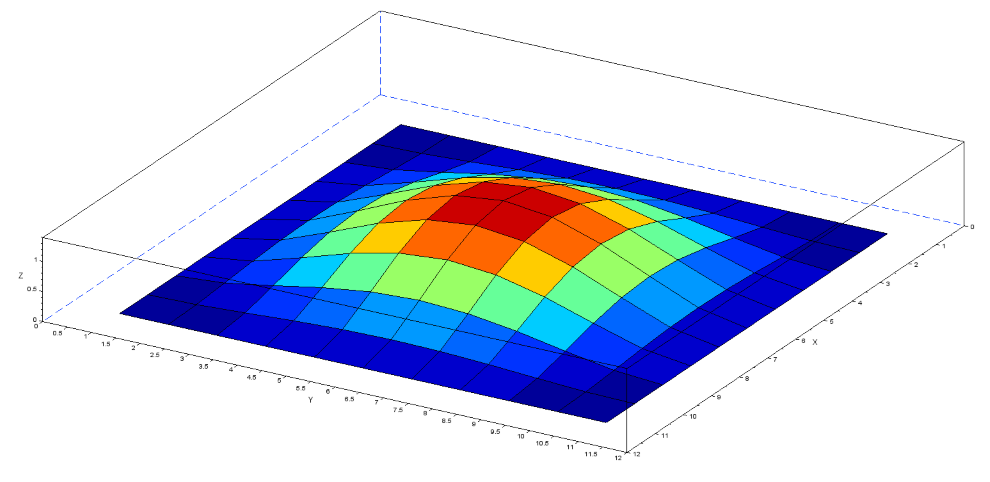
計算結果を以下に示します。最も大きな変位は中央部で1.4ｍｍとなりました。

上記FEM計算結果の検算として以下の理論式により自重変形量（参考文献[3]）を求めます。

　ωmax=0.0138 *q * a4 / (E*t3)=1.35mm

    q：面圧 13.7Pa（密度2800㎏/m3*板厚0.0005mm*G)

    a：１辺長さ 0.5m

    E：縦弾性係数　70GPa(アルミ)

　　t：板厚0.5mm

理論式1.35mmに対しFEM計算結果が1.4ｍｍと十分な一致を見ることが出来ました。

---

２.２　動的解析(振動荷重)

　まずは1.1項で設定した減衰力が妥当かを確認するため、前述Scilabモデルを用いてDetail2で計算した１次モードの様子を調べてみます。

　最初に1次モードになる外力を加え、その収束の様子を見ます。今回のScilab計算では1次モードに対応する{ξ₁}は固有ベクトル[P]の第191列でした。剛性行列[Kf]に{ξ₁}を掛けることで1次モードに変形する外力を計算します。計算結果をScilabモデル中のIni_forceとします。

　計算した結果が以下です。中央部の凸部量は25ｍｍで、１次モードと一致しています。

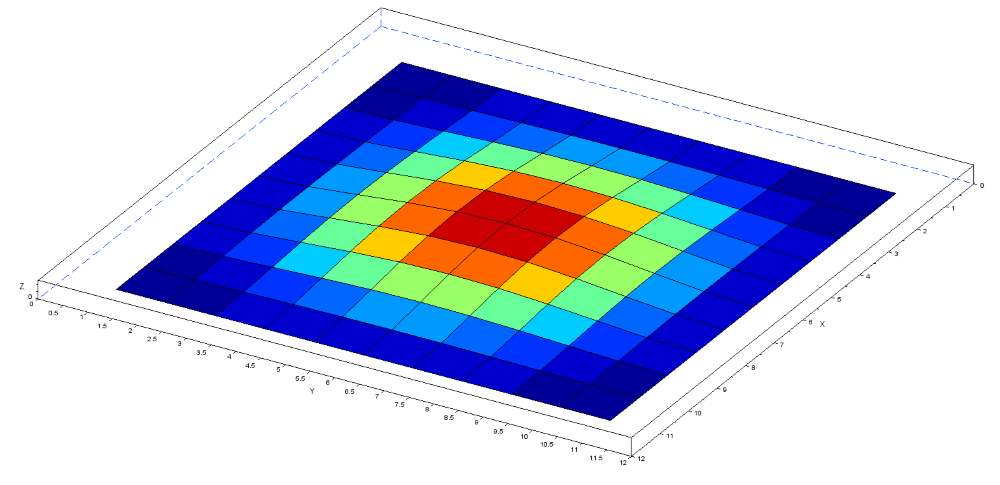
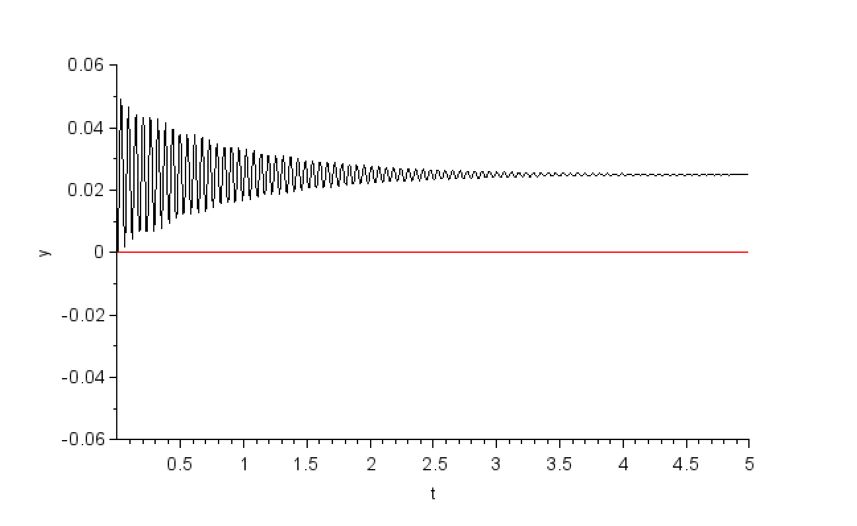
また動的解析の収束の様子を示します。

収束具合は理論上e^-ζωtとなりますので、今回の時定数は

    1/(ζω)=1/(0.01*2π*17.16)=0.93秒

となります。下図は振動しているので見ずらいですが、おおよそその程度の時定数と見て取れます。

　続いて下図Scilabモデルを用いて１次モードに共振周波数17.16Hz(固有値)を加えた場合の様子を調べてみます。前回モデルとの変更点は「Ini_force」の部分に正弦波ブロックを加えただけとなります。

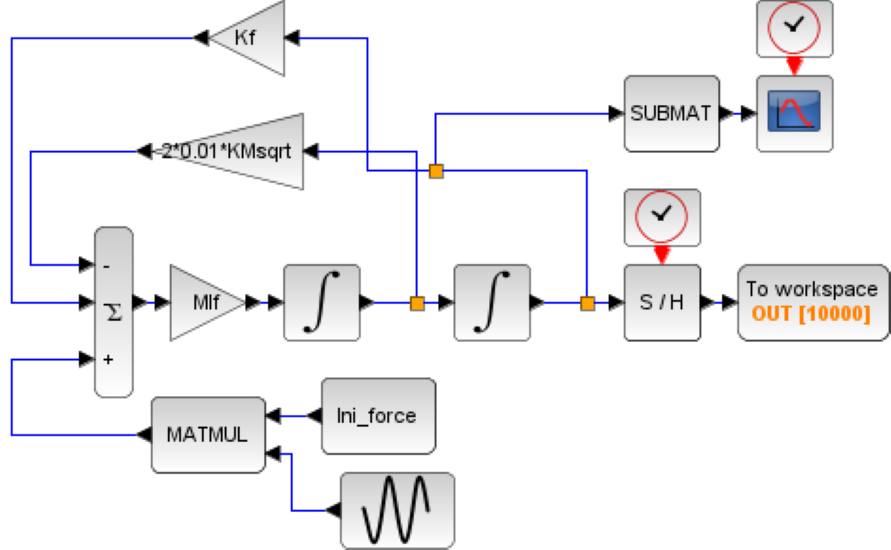
　計算した結果が以下です。共振点の理論上のピークは1/(2ζ)=50倍となります。計算結果では、中央部の凸部は1120mm位(振動の中間位)で静的25mmの約45倍で理論とおよそ一致しています(ピーク値で見ると約50倍となっています)。

　また収束時定数もおよそ理論と一致しているようです。

　ここまでの検討により上述Scilabモデルの動的妥当性が確認出来ました。

　実際の現場では構造物が破壊するか否かが問題となるため、動的挙動中の内部応力が重要な解析対象となります。detail3にて動的挙動中の内部応力を求めたいと考えます。

---

参考文献

[１]機械構造 振動学 MATALBによる有限要素法と応答解析　小松敬冶 著　森北出版株式会社

[２]機械振動学　岩田佳雄・佐伯暢人・小松崎俊彦 共著　数理工学社

---