1.1 chtMultiRegionFoamの性能確認
Detail1にて設定した前方投影面積の有効倍数3.0について検討する前にそもそものOpenFoamの熱流体計算(chtMultiRegionFoam)の確からしさを検討してみます。
本文に用いた以下の式より熱伝達率hは速度の平方根に比例することが知られています。
h=0.57*Pr0.385 *k/R*(2*R*U/ν)1/2 (関連文書[1])・・・(1)
この点をサーボ・モータの計算で確かめてみます。
サーボ周辺の速度を1m/s、5m/s、10m/sと変えた場合の平衡温度を計算してみます。
(1)式によれば10m/sでは1m/sよりも√10倍熱伝導率が増加し、温度としては1/√10倍になるはずです。
尚本文と同じ解析モデルを使用すると計算時間が2週間掛かると推定されるため、以下の大幅な改修を行います。
・メッシュ粗さ
本文のモデルでは最も小さいメッシュサイズが1mm四方でしたが、6.6mm四方に変更
・クーラン数
本文モデルではクーラン数Max0.3とし、時間間隔はOpenFoamの自動調整にしていたものをクーラン数0.7で時間間隔を直接固定指定。これにより部分的に小さいメッシュ部分ではクーラン数が1を超えている。
・個体物性値密度修正
計算時間短縮のため、個体物質の密度を1/5にし、収束にかかる時間を1/5に短縮。計算結果は時間軸を5倍にして修正表示。
1.2 速度別計算
まず前項にて作成したモデルと本文モデルの違いを明確にするため1m/sでの計算結果を比較します。結果、新しいモデルでは本文モデルよりも10℃程度平衡温度が上がってしまいました。メッシュを粗くしたためと考えられます。
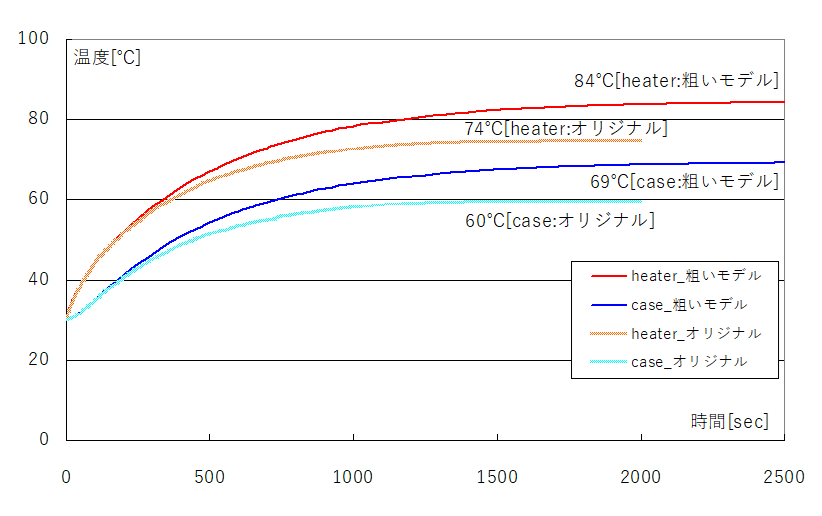
この結果を踏まえて、新しいモデルを用いた速度別計算結果を以下に示します(上側:1m/s、下側:10m/s)。
結果、流れの様子は同じようで、速度上昇により乱流が増えている様子はありません。
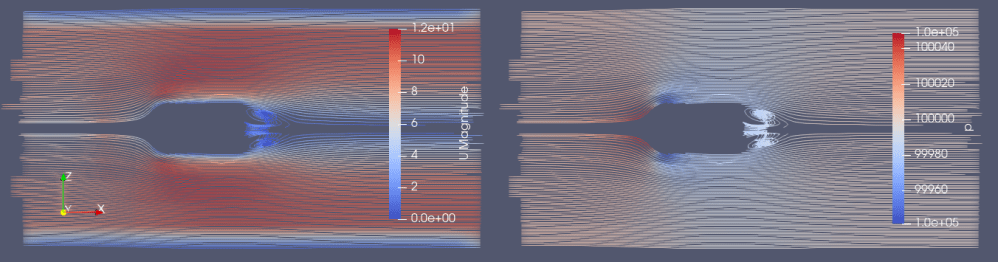
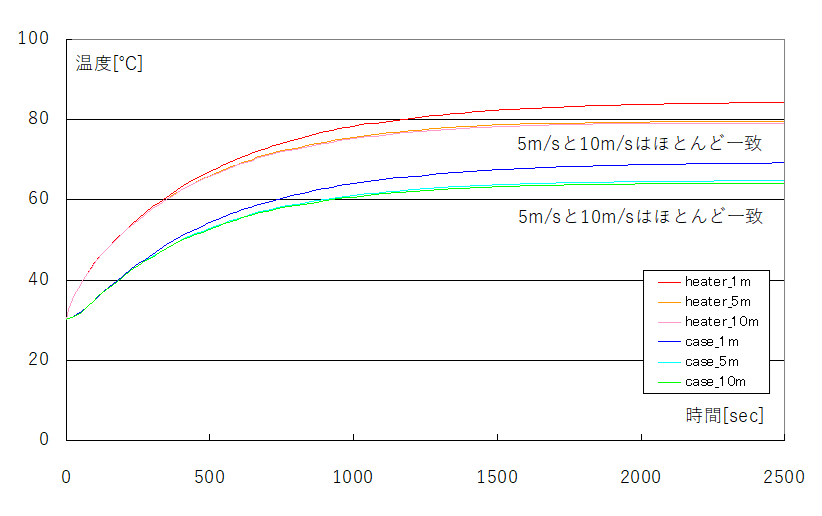
エクセル結果より速度別のヒーター部の平衡温度は84℃(1m/s)、80℃(5m/s)、79℃(10m/s)といった結果となりました。
これは当初予想した1/√10を全く満足していません。
(この比較を行う際はcase温度と周囲温度の差分を見る必要があります。)
・1m/s ΔT=69-30=39℃
・5m/s ΔT=65-30=35℃
・10m/s ΔT=64-30=34 ←速度が反映されているのならば、39/√10=12℃になってほしい値
結果、当事業所で実施した計算条件ではchtMultiRegionFoamが実験式である(1)式を十分反映出来ていないと考えられます。
1.3 熱計算
前項結果の原因を考えるため、外気流による冷却の仕組みを考えてみます。
伝熱には以下の3つの型があるとされています。
・伝導 例:個体同士の接触による熱伝搬
・伝達 例:気体による個体表面の熱伝搬
・輻射 例:物体の温度による熱放射
本モデルにおいてheater-case間は伝導、case-周囲空気間は伝達と言えます。
ここで伝達においても周囲速度が「0」で自然対流も発生しなければ、それは気体による伝導と言えます。
サーボ周りの冷却を極端な概略図で示すと下図のごとく、サーボ周りの境界層では静止空気による伝導が起こり、境界層端まで熱伝導率kに従った温度降下が発生し、境界層を超えると周囲気流が急速に熱を奪っていくという状況と考えられます。
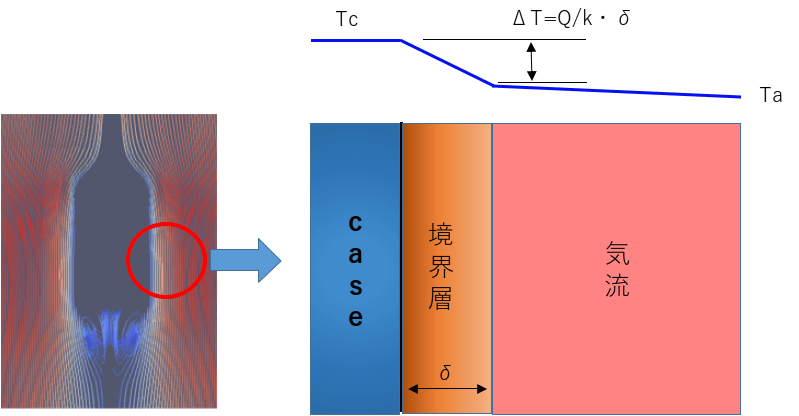
上図のように気体による冷却のシミュレーションでは境界層の模擬が非常に重要となる訳ですが、以下が主な原因となって今回の計算では速度を変えても冷却効果が速度の平方根に比例していないと考えられます
・境界層の模擬
解析のメッシュ粗さ6.6mmでは速度に応じた境界層の模擬が出来ていない。
・乱流境界層の模擬
流体の計算方法が層流(laminar)方式であり、乱流境界層を模擬していない。
(乱流境界層の方が層流境界層よりも相当大きな熱を伝導するそうです。)
例えば境界層δが1mmとすると今回の解析では
ΔT=2W/[0.0286W/(mK)・S]*1mm=47℃ (S=2cm*2.5cm*3))
この時Ta=30℃とするとケース温度は77℃。
もし境界層δが2mmの時はケース温度が123℃と概算されます。
境界層の厚さに非常に敏感になる様子が見て取れます。
(参考:chtMultiRegionFoamで熱伝導率は粘性係数と定圧比熱及びプラントル数から計算している模様。)
1.4 有効面積倍数3について
前述の検討より本文で実施したOpenFoamのchtMultiRegionFoamは十分な速度模擬が出来ていません。
そもそも1m/sの計算結果の確からしさも確認出来ていません。
この観点から有効面積倍数3についても熱伝導率を実験式(1)を用いたい場合のフィッティングであり、速度が変われば変わってしまう値となります。
以上より当事業所で行う計算のメッシュ粗さでは非常に限られた条件(メッシュ粗さに対し境界層が十分厚い)のみ有効で、実用性に乏しいものとなっています。
[追記]
chtMultiRegionFoamのソルバーをlaminar(層流モデル)からRAS(乱流モデル)に変え、形状を円柱にすることで実験値との比較を検討してみました(detail3)。結果、レイノルズ数の範囲限定はありますが速度模擬が出来るようになりました。
尚この変更は当事業所独自の試算のため、試験による検証が必要です。
以下に乱流モデルの変更を行った場合のサーボ・モータの熱解析をやり直した結果を示します。結果、上昇温度が速度の平方根に逆比例していることを確認出来ました。

・メッシュ粗さ:6.6mm四方(変更なし)
・クーラン数:クーラン数0.7で時間間隔を直接固定指定。
・乱流モデルをlaminarからRASに変更(詳細はdetail3に従う)。
・個体物性値密度修正:計算時間短縮のため、
個体物質の密度を1/100にし、収束にかかる時間を1/100に短縮。
計算結果は時間軸を100倍にして修正表示。
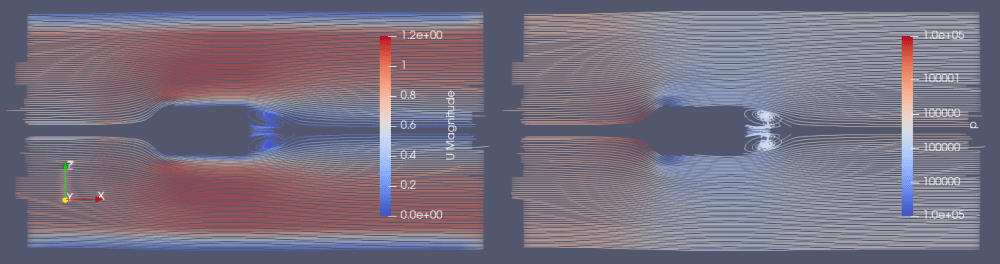
10m/sと1m/sの流れの様子に大きな違いは見られません。
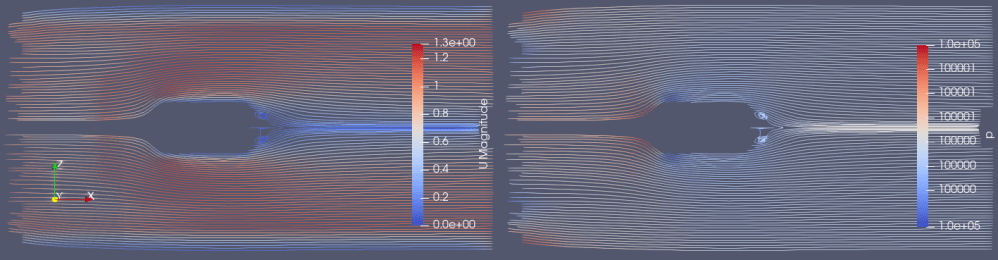
〇速度1m/s:y+関数10
(適正30~300を外れているが共通メッシュのためにそのままとした)
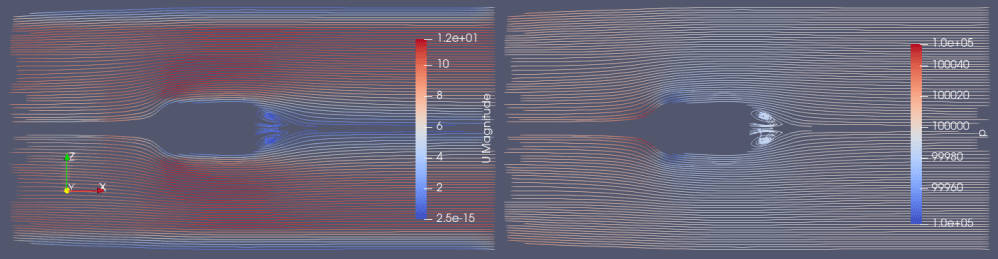
〇速度10m/s:y+関数70(適正30~300)
参考文献
[1]JSMEテキストシリーズ 電熱工学 日本機械学会 丸善出版
改訂記録
A改訂 2025.4.18 全面改訂
