１．解析解(机上計算)による検証

１．１　1次熱伝達の解析解

　OpenFaomの検証を行う上で、まず最も単純な熱モデルを作成して熱解析の基本を振り返りたいと思います。

上図における熱伝達の式は以下となります。

　(cρＶ)dT/dt = Q_in-Q_out　・・・(1)

　  c：比熱[J/kg/K]

　　Q_in：発熱量[W]

　  Q_out：放熱量[W]

放熱量Q_outは一般的に以下の式で表現出来ます。

  Q_out = hSΔT = hS(T-T_a)　・・・(2)

　　ｈ：熱伝達率[W/m²/K]^※１

　　Ｓ：放熱面積

　　T_a：雰囲気温度

Q_inが定数の場合、(1)(2)より以下の式が熱伝達の式となります。

　(cρＶ)dT/dt = Q_in-hS(T-T_a) ・・・(3)

この式は時間に関する1次微分方程式であり、解くと以下となります。

本文のサーボ・モデルをこの式に当てはめて見ます。

  Q_in = 2[W]

  ｈ=50.2[W/m²/K] ^※１

  S = 0.8cm*π*1.2cm = 3.02e-4

  c = 419[J/kg/K]

  ρV = 8900*(0.8cm)²*π*1.2e-6

　　※１：参考文献[1]の3.4.2項より

　　h=0.57*Pr^0.385 *k/R*(2*R*U/ν)^1/2

　　　Pr：プラントル数　空気0.7

　　　ｋ：熱伝導率　空気0.0286W/(mK)

　　　Ｒ：円柱半径 8mm

　　　U：遠方周囲流速 1m/s

　　　ν：動粘性　空気2e-5 m²/s

よって最終到達温度差ΔTは

　ΔT=Q_in/hS = 132K

時定数τは

  τ= cρV/(hS) = 593秒

(4)式はエクセルでも表示出来ますが次項の兼ね合いからScilabで解いて見ます(初期温度30℃)。

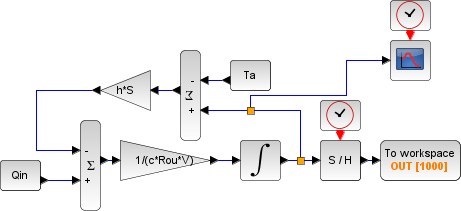
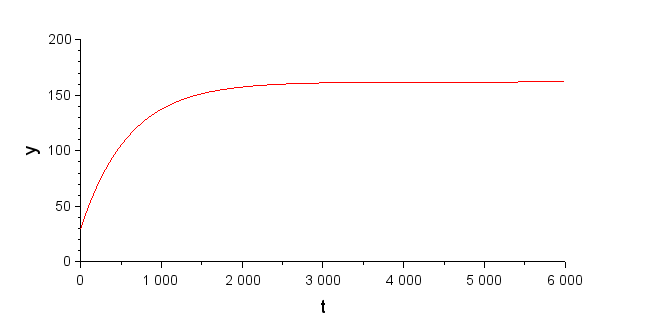
時定数約593秒(63％に到達する時間)で最終的に162℃に収束していく様子が伺えます。

但しこの結果では昇温が早すぎてOpenFoamの結果とは乖離した結果となっています。

---

１．２　連立熱伝達式の解

　1.1項の計算は非常に簡略したモデルのため、ケースを模擬出来ていません。ここではケースをモデルに組み込んでみます。

上図における熱伝達の式は以下となります。

　(c_mρ_mＶ_m)dT_m/dt = Q_in-Q_cont　・・・(5)

　(c_cρ_cＶ_c)dT_c/dt = Q_cont-Q_out　　

  Q_cont=h_cS_c(T_m-T_c)　　　　　　　

  Q_out = h_oS_o(T_c-T_a)　　　　　　　

　  c_m=419：モータCu比熱[J/kg/K]

　  c_c =880：ケースAL比熱[J/kg/K]

　 ρ_m=8900：モータCu密度[kg/m³]

　 ρ_c=2770：ケースAl密度[kg/m³]

　 V_m=0.008²*π*0.012：モータ体積[m³]

　 V_c=((20+36)*2*25*2+20*36*2)*1e-9：ケース体積[m³]　厚み２㎜

　 Q_in=2：発熱量[W]

　  Q_out：放熱量[W]

　 ｈ_c=0.0286/.0001：モータ-ケース間熱伝達率[W/m²/K]　

　　　　空気の熱伝導率x空気0.1mm(JISすきまばめ緩合９等級を想定)を仮定

　 Ｓ_c=(0.013+0.016+0.013)*0.012：モータ-ケース間接触面積(FreeCADモデルと同じ)

　 ｈ_o=44.9：ケース-雰囲気間熱伝達率[W/m²/K]　1.1項と同じ

　　　h=0.57*Pr^0.385 *k/R*(2*R*U/ν)^1/2

　　　Pr：プラントル数　空気0.7

　　　ｋ：熱伝導率　空気0.0286W/(mK)

　　　Ｒ：ケース幅の半分 10mm(円柱の式を直方体に拡大適用)

　　　U：遠方周囲流速 1m/s

　　　ν：動粘性　空気2e-5 m²/s

　 Ｓ_o=0.02*.025*3.0：ケース放熱面積(前方投影面積の3.0倍(適当)とした）

(5)式は机上計算による解法は困難なためScilabで計算して見ます。

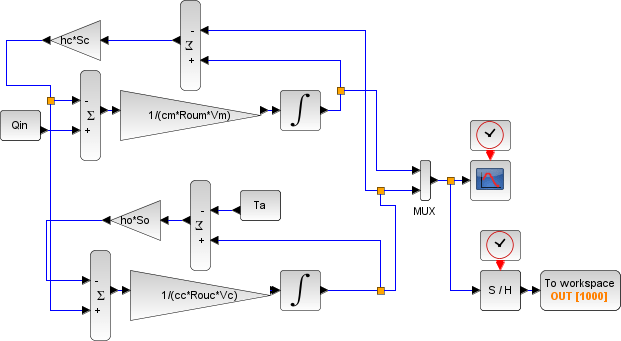
結果は以下となりました(赤線：モータ温度、青線：ケース温度)。

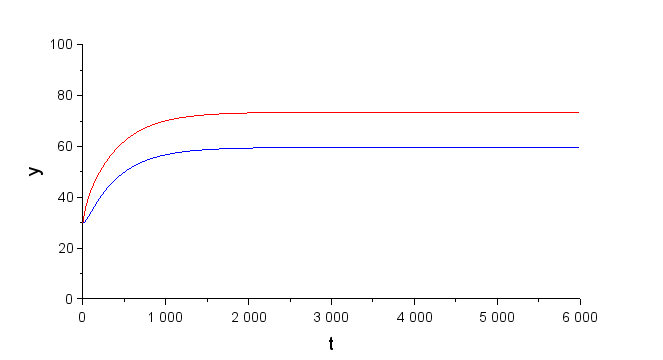
ケースにより放熱面積が増えているため1.1項の結果よりもモータ温度の昇温が遅くなっています。

尚上図の収束温度及び初期傾斜は以下の式で求められ、上記グラフと一致しています。

・ケース温度上限：T_c=T₀+Q_in/h_oS_o=59.7℃(緑線)

・モータ温度上限：T_m=T_c+Q_in/h_cS_c=73.6℃(黒線)

・モータ温度傾斜(t=0) Q_in/ c_mρ_mV_m=0.222K/sec

　以下にOpenFoam計算結果、1.1項及び1.2項のScilab計算結果をエクセルにまとめて示します。

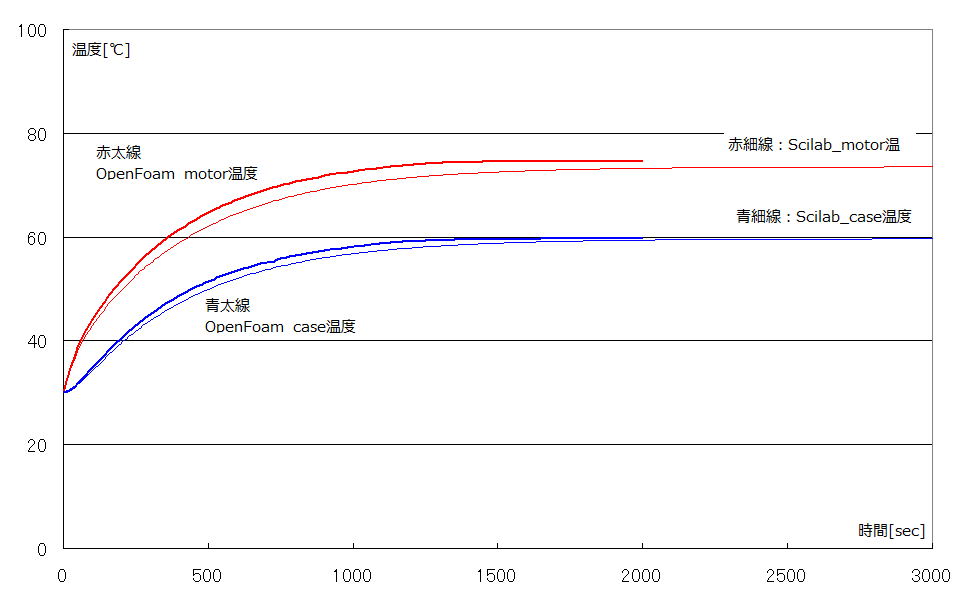
　結果、OpenFoamの計算結果とScilabを用いた検算がおよそ一致しました(OpenFormのモータ温度とScilabとで若干の差が出ていますが、計算時間を伸ばしていくと更に近づく傾向です)。

これはScilab計算において放熱面積を前方投影面積の3.0倍に設定したためです(以後有効面積倍数とよびます)。この値は残念ながら机上計算で求めることは困難と思われ、実運用では試験または流体解析が必要となると考えます。

　一方この有効面積倍数さえ把握出来れば長時間のPC計算が必要なOpenFoamを使わなくても、Scilabによりごく短時間で計算出来ることとなります。

　Detail2にて有効面積倍数3.0をもう少し検討してみます。

---

参考文献

[1]JSMEテキストシリーズ　電熱工学　日本機械学会　丸善出版

---