「Step2」
(1)静的外力による変形
Step1の計算にて説明していませんでしが、固有値計算は以下に示す要領で実施しています。
(要点をまとめましたが、これでは説明不足なので別リンク(Detail)で説明致します。)
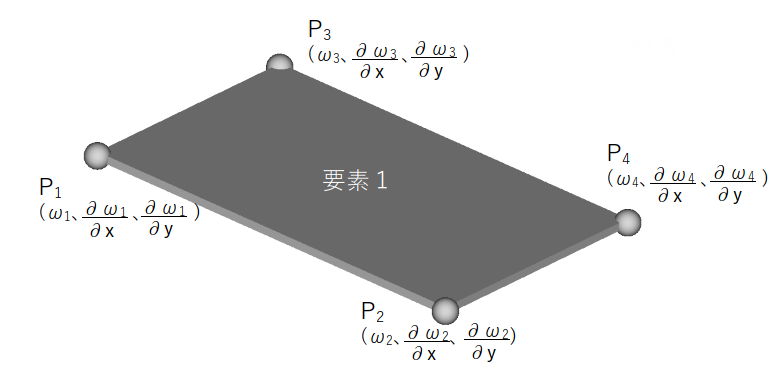
・10×10マスに分割した四角形が最小単位の要素となります。この一要素の端点P1、P2、P3、P4の面に垂直な方向の変位をω1、ω2、ω3、ω4とし、その変位の傾きを∂ω1/∂x、∂ω2/∂x、∂ω3/∂x、∂ω4/∂x、∂ω1/∂y、∂ω2/∂y、∂ω3/∂y、∂ω4/∂yと設定します。
・この12個の入力変数から式(1)を用いて、内部応力と境界力(12個の境界力が出力)を推算します。
・上記入出力計算を全100要素に実施し、全ての要素が辻褄のあう状態を探します。やり方としては全要素を対等な行列要素として結合し、全要素が同時に辻褄の合う状態を計算します。
・以上の計算から初期条件を与えた状態での境界力が計算されます。これは変位を与えた時にばね反力が得られる状況と一致しており、上述行列を剛性行列[K]として扱っていきます。
・続いて質量を行列で表現出来たとして、それを質量行列[M]と表現します。すると下記の式より固有振動数が求められます。
f=1/2π*√([K]/[M])
この式はイメージであって、実際には[K]と[M]は行列のため、特別な扱いが必要となります。
・上述の一連の動きをScilabのXcos(MatlabのSimulink相当)で表現すると以下となります。
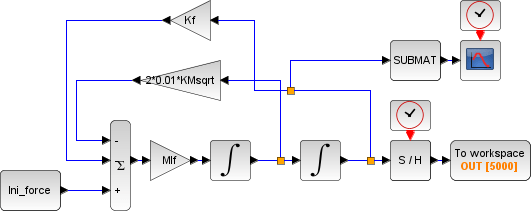
モデルの特徴を羅列してみます。
・図中の「Kf」が剛性行列[K]、「MIf」が質量行列[M]の逆行列に対応します。
・「∫」は1回の時間積分を意味します。
・「2*0.01*KMsqrt」は減衰率1%の減衰力、KMsqrtは√([M][K])を表しています。
(減衰行列を理論計算により表現することは難しいそうです。
ここでは単体2次応答の減衰力である2ξ√(KM)の模倣で行列表現してみました。
これは当事業による1案で、いろいろな案があります。詳細はこちら(Detail2)に示します。
尚1%は一般的構造物の減衰率で個別調整が必要な値です。
・「Ini-force」により外力が定義出来ます。
・時計マークのある2つのブロックは出力ポートとなります。
・モデルの構成は「変位」に剛性行列[Kf]をかけることでばね荷重を計算し、それを質量行列[Mf]で割ることで「加速度」を算出します。加速度を2回積分することで「変位」を算出します。これを一定時間刻みでループさせることでモデル上の時間を変化させて行きます。
・大事な点はこのXcosモデルにより登場してくる全変数の時間的変化を把握出来る点となります
実際に外力として自重分を加えた計算結果を示します。
計算結果から最も大きな変位は中央部で1.41mmとなりました。
一方後述理論値※1は1.35mmとなり、おおよその一致を示しています。

※1:理論式による自重による変形量(参考文献[3]による)
ωmax=0.0138 *q * a4 / (E*t3)=1.35mm
q:面圧 13.7Pa(密度2800㎏/m3*板厚0.0005mm*G)
a:1辺長さ 0.5m
E:縦弾性係数 70GPa(アルミ)
t:板厚0.5mm
(2)振動する外力による変形
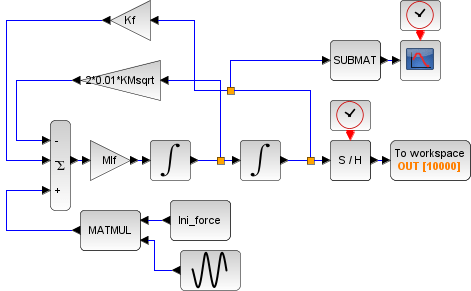
前項の計算よりXcosのモデルは現実を十分模擬できていることを確認しました(当事業所の計算はこのレベルの模擬となります)。そこでこのXcosモデルを使い、外力を振動するモデルに書き換えます。そのモデルが以下となります。
変更点は「Ini_force」の部分に正弦波ブロックを加えただけとなります。
道具の準備が整いましたのでStep2の目的である風による外力を以下のように仮定します。尚この仮定は速度が早すぎるという若干無理くりなところがあり、あくまで計算用サンプルとご理解ください。
・円柱周りの風速は70m/s(250km/h)。よって円柱後方に発生するカルマン渦の周波数は以下。
f=0.2*V/D=0.2*70m/s/ 1m = 14Hz
・風速70m/sでの動圧は1/2*1.225*702=3001Pa。このうち5%程度の変動が円柱後方で発生すると仮定すると3001*5%=150Pa(この5%に関しては無理な設定となっており、当HPのOpenfoam流体解析例では違った状況を示しています。詳しくはこちらをご覧下さい)。
・以上より円柱後方には圧力0~150Paが14Hzの周期で付加させると仮定します。
・外力を振動させる前に静的解析を実施してみます。図-2のモデルに150Paの負圧を加えてみます。結果は中央の変位で15.1mmとなりました。負圧のため、凸に変形していますが、値は前回の計算と圧力から外挿しても妥当と見えます。

・続いてこの静的荷重を14Hzで振動した場合の計算を実施して見ます。結果は中央で振幅最大約45mmに5秒程度で収束しました。

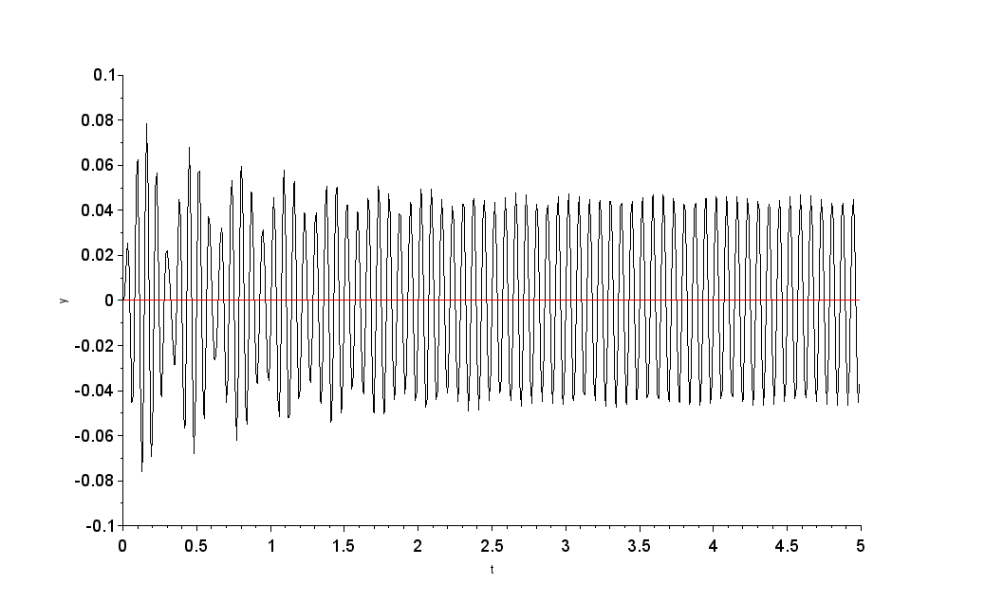
下記ばね-マス系の共振振幅の公式を用いて上記計算結果の検算を行います。下式よりGainは2.99倍となり静的荷重時変位15.1mmの2.99倍である45.1mmが検算値となり、上記計算結果と十分な一致を示しています。
|G(jω)|=[(1-Ω2)2+(2ζΩ2)2]-1/2=2.99
Ω=ω/ωn
ω:印加周波数14Hz
ωn:固有振動数17.16Hz
ζ:減衰率1%
尚上記時間的変化は減衰行列の設定に強く依存します。ここでの計算例はあくまで減衰力を「2*0.01*KMsqrt」と仮定した場合のものであり、試験値や他実績値によりその挙動を確認する必要があります。
(3)内部応力の様子
前項にて共振手前での薄板の挙動を解析しました。共振周波数17.16Hzの80%にあたる14Hzでも共振の影響で約2.99倍となることを確認してきました。共振で問題となるのはその状態での構造破壊となります。それでは14Hzの外乱でどの程度の応力が発生しているかをScilabを用いた解析で見ていきたいと思います。
結果を以下に示します。尚この辺りの具体的計算の様子はこちら(Detail3)に示します。
応力計算結果:フォン・ミーゼス 111MPa(下図)
主応力 125MPa
σx 125MPa

一方後述理論値※2は138MPaとなり、十分一致しています。この辺りの考察はFreeCADの解析でも実施してみます。
※2:理論式による薄板曲げモーメント及び応力(参考文献[1]による)
Mxmax=0.0513 *q * a2 = 5.75Nm
σxmax=Mxmax*6/t2 = 138Mpa
ωmax=0.0138 *q * a4 / (E*t3)=44.3mm
q:面圧 150Pa*2.99
a:1辺長さ 0.5m
t:板厚0.5mm
結果として得られた125MPa(18ksi)ですが、例えばアルミ2024-T42材の場合、参考文献[2]より以下の特性と読み取れます。この場合静的には十分耐えられそうですが、疲労計算をすると厳しそうです。
Ftu(引っ張り終局応力)= 393MPa(57ksi)
Fty(引っ張り降伏応力)= 234MPa(34ksi)
Fsu(せん断終局応力) = 234MPa(34ksi)
FreeCADの解析で薄板を固定しているリベット周りを更に解析することで疲労強度を検討してみようと思います。
つづく「Step3」においては敢えて面圧を偏らせた場合の薄板の動的変化を計算してみます。
参考文献
[1]工学基礎 材料力学 清家政一郎 著 共立出版
[2]MIL-HDBK-5J 31 January 2003 METALLIC MATERIALS AND ELEMENTS FOR AEROSPACE VEHICLE STRUCTURES
