「テーマ」
・風による外板の共振を計算してみます。
「方針」
Step1:Scilab※1により外板の固有振動数を求めます。
Step2:Scilabにより風による外力を模擬し、外板の動的運動を推算します。
Step3:偏った面圧を加えた場合の外板の動的運動を推算します。
応用例:動的運動解析の応用としてフラッター解析をトライします。
「想定モデル」
・500x500x0.5mm アルミ薄板
・直径1mの円柱に70m/s(250km/h)の気流が当たるときの風下側の気流がはがれだしているあたりにおける乱流を外力に想定します。
※1 Scilab:フランス研究機関INRIAの作成した無料の数値解析ソフトウエア

「Step1」
(1)Scilabによる薄板2Dモデル
500x500mmを10x10マスに分割しています。
尚2Dとして厚さ方向の模擬はしていません。

(2)Scilabにおける計算内容
薄板解析に用いた基本方程式は以下となります(薄板の重調和方程式)。

ωは板の面外変位(面に垂直方向の変位)を示し、qは面圧となります。
Dは曲げ剛性で以下となります。
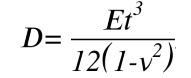
式中のEはヤング率、tは板の厚さ、はポアソン比を意味します。
本式の特徴として変位ωは板に垂直方向の極微変形であり、変形に伴う要素面の伸びは考慮されていません。更に薄膜の張力は考慮されていないです。よって大変形に対しては解析誤差が大きく、一般的には変位量ωが薄板の厚み程度までが許容領域と言われています。
FEM(有限要素法)の解法として変位法※2を用いており、プログラムを作成する上での詳細は参考文献[1]に従いました。
※2:1要素内(四角要素1つ)にて変位関数を仮定し、境界条件から内部変形、応力を計算する理論。
(3)Scilabによる固有振動数の計算
500x500x0.5mmの薄板の周囲四辺を固定した場合の固有振動数をScilabを用いて計算して見ました。結果をモード次数5までを以下に示します。FEMとしては粗い10x10マスでも理論値との十分な一致を示しています。
1次モードでは凸部が一つ、2次モードでは凸部が2つ、3-4次モードでは凹凸部が4つと規則正しく増加していく様子が見て取れます。この解析結果では見ずらいですが5次モードでは5つの凹凸部が形成されます。正方形において対称性を維持しながら凹凸部が増えていくようです。
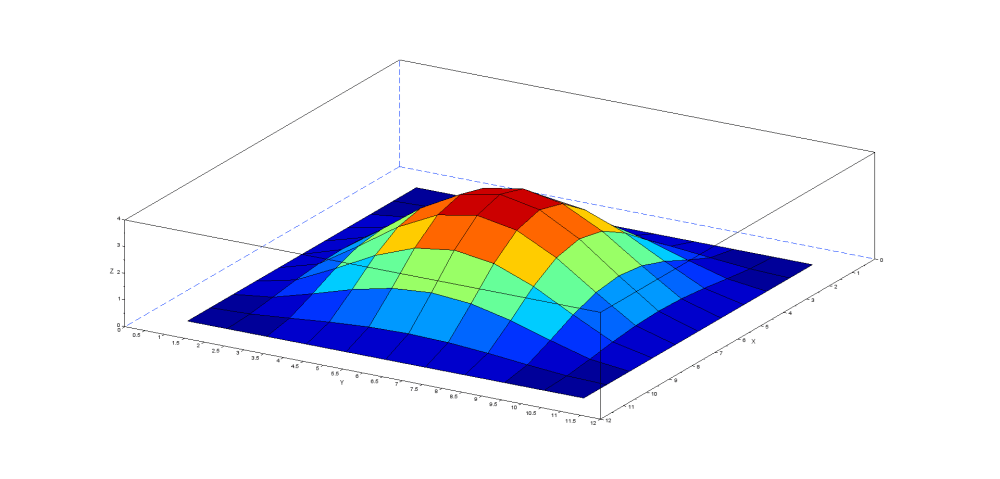
1次モード:固有振動数 17.16Hz(理論値 17.33Hz)
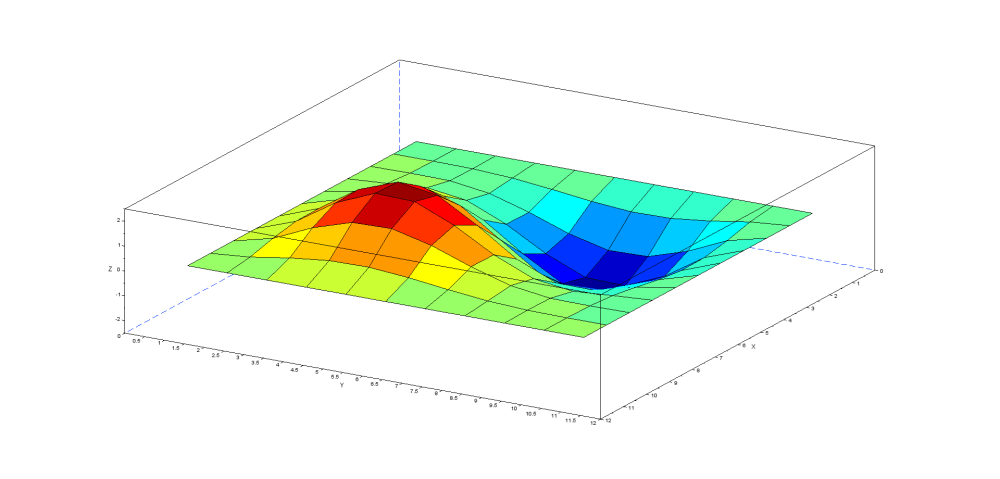
2次モード:固有振動数 34.91Hz(理論値 35.36Hz)
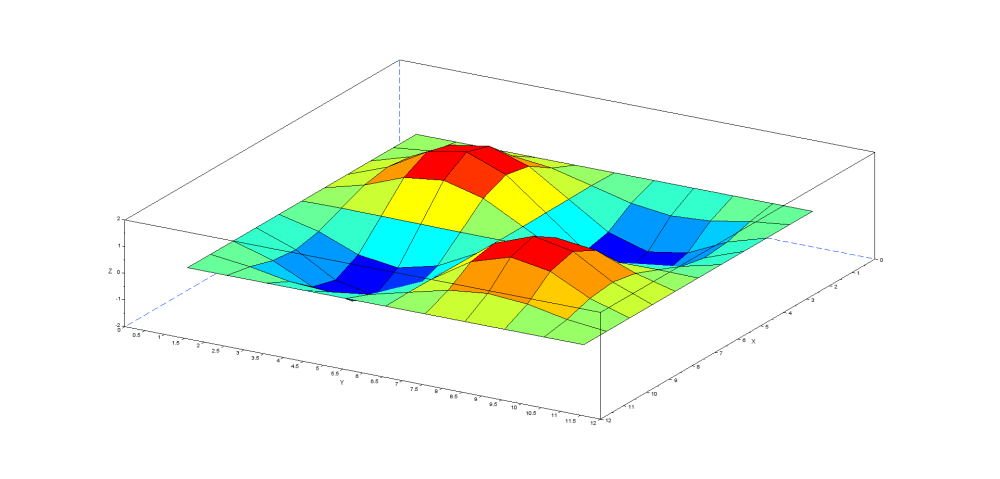
3次モード:固有振動数 50.64Hz(理論値 52.16Hz)
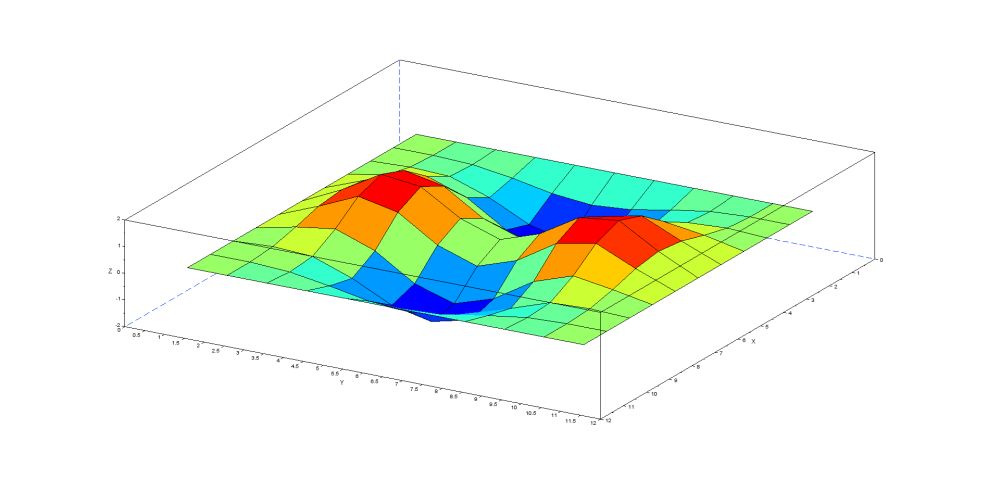
4次モード:固有振動数 62.62Hz(理論値 63.38Hz)
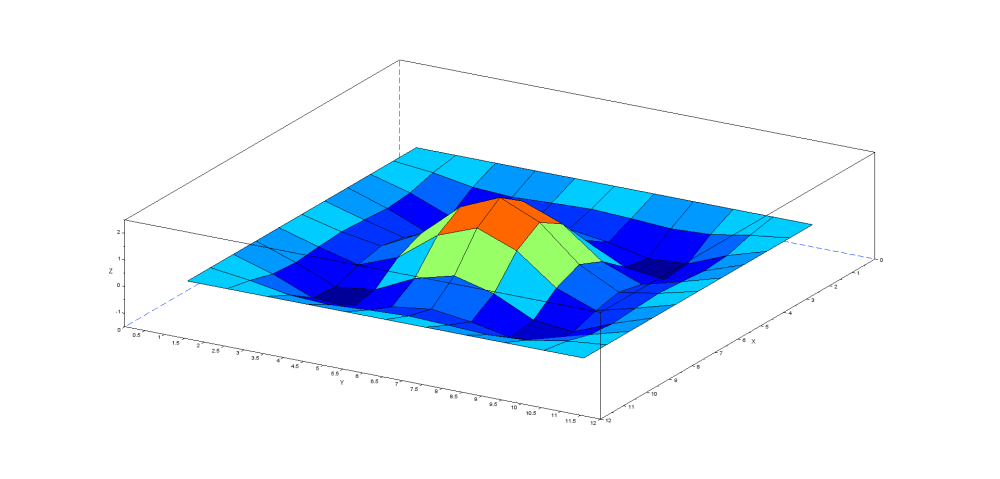
5次モード(Z方向反転):固有振動数 63.00Hz(理論値 63.67Hz)
尚併記した理論計算値は以下の式から計算しました。式は参考文献[2]に拠ります。
固有振動数計算理論式

λ2=35.99(1次)、73.41(2次)、108.3(3次)、131.6(4次)、132.2(5次)
a:板の1辺の長さ[0.5m]
D:曲げ剛性(式(2)と同じ) [E=7*10^10Pa][ν=0.3](Scilabの計算でもこの値を使用)
ρ:密度[2800kg/m3](Scilabの計算でもこの値を使用)
t:板厚[0.0005m]
以上でStep1の目的であった固有振動数が得られました。結果として約17Hzに最初の共振点が現れます。外力がこの周波数に近い振動をすると、共振の発生が推定されます。Step2にてその様子を考察していきます。
補足となりますが10x10マスを増やしていくと更に緻密な描写が得られますが、目的である固有振動数は10x10マスで十分のようです。一方、これ以上マスを細かくしていくとPCの性能上Step2での解析がメモリーオーバーしてしまいます。当面、当事業所での解析はこのレベルが限界となります。
参考文献
[1]機械構造 振動学 MATALBによる有限要素法と応答解析 小松敬冶 著 森北出版株式会社
[2]機械振動学 岩田佳雄・佐伯暢人・小松崎俊彦 共著 数理工学社
改訂記録
A改訂 2025.3.22:円柱外板位置を後方から前方に移動
