「Step2:薄板三角形の解析」
1.モデル
検討対象は他解析と共通とするため以下で統一しました。
・500x500x0.5mmの三角形のアルミ板
・1辺のみ固定
2.解析手段
step1の検討でメッシュ4のやり方が最も信頼性のあることを確認していますので、ここではメッシュ1とメッシュ4を用いて計算してみます。
・メッシュ1:Scilab 10×10マスで三角形を模擬。斜辺の模擬度が低い欠点を持つ。
・メッシュ4:Gmesh 板厚10倍 設定[要素次数2nd、要素最大10mm、要素最小0.1mm]
メッシュ4.1:固有値解析:密度を100倍に修正。
メッシュ4.2:変形量解析:荷重を1000倍に修正。
メッシュ4.3:応力解析 :荷重を100倍に修正。
3.固有値解析
薄板三角形の固有値の理論式は見つけられませんでした。
そこで参考に四角形の場合の計算結果を示しておきます。
f1=1.68Hz、f2=4.12Hz、f3=10.33Hz、f4=13.23Hz、f5=15.01Hz
メッシュ別の固有値解析の結果(1~5次モード)を以下に示します。
結果、メッシュ1とメッシュ4の計算結果はほぼ一致していることを確認出来ました。
このためメッシュ1であるScilab計算結果を動的解析に使用しても問題なさそうです。
・1次モード(四角形の場合の理論値1.68Hz)
メッシュ1=2.69Hz、メッシュ4.1=2.99Hz
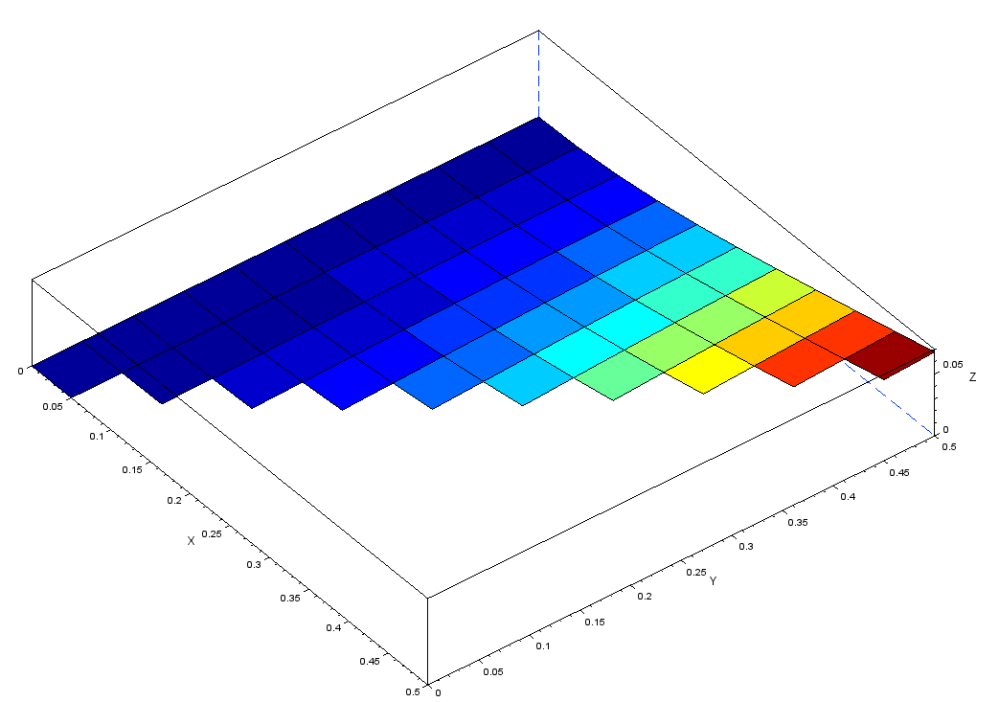

・2次モード(四角形の場合の理論値4.12Hz)
メッシュ1=10.17Hz、メッシュ4.1=11.38Hz


・3次モード(四角形の場合の理論値10.33Hz)
メッシュ1=14.19Hz、メッシュ4.1=15.90Hz
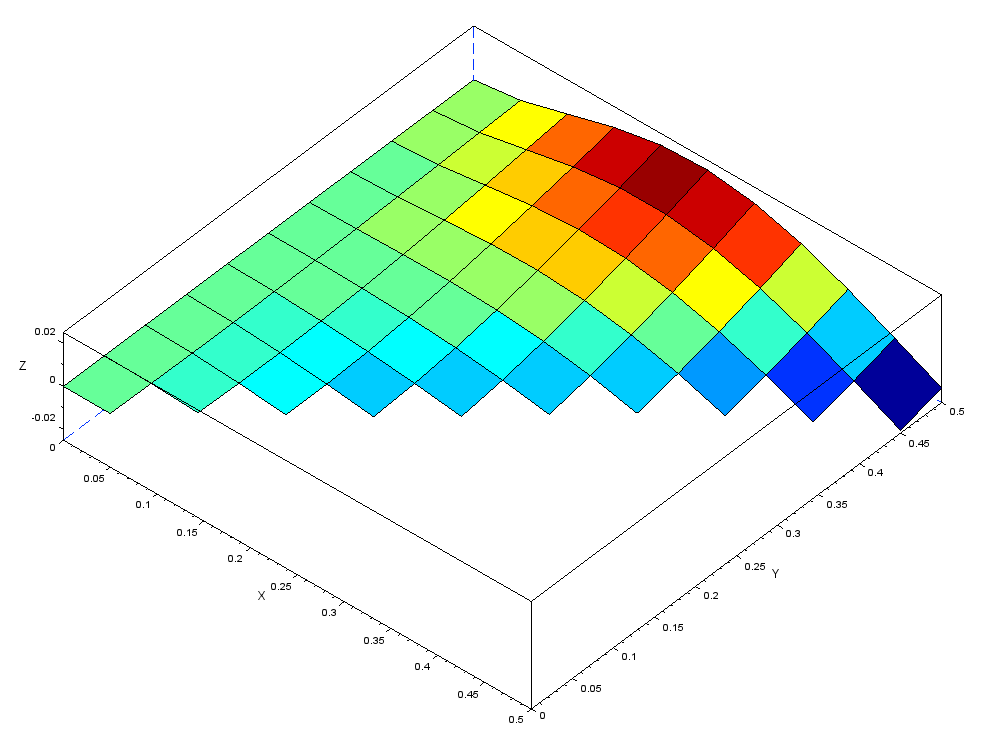
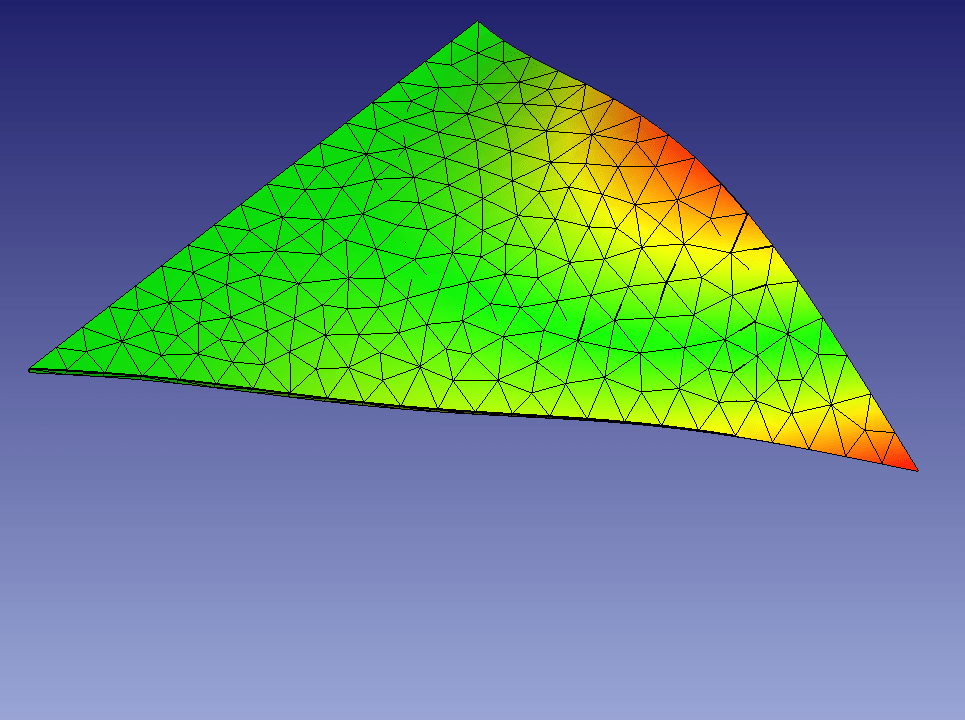
・4次モード(四角形の場合の理論値13.23Hz)
メッシュ1=24.10Hz、メッシュ4.1=27.38Hz


・5次モード(四角形の場合の理論値15.01Hz)
メッシュ1=33.19Hz、メッシュ4.1=37.40Hz
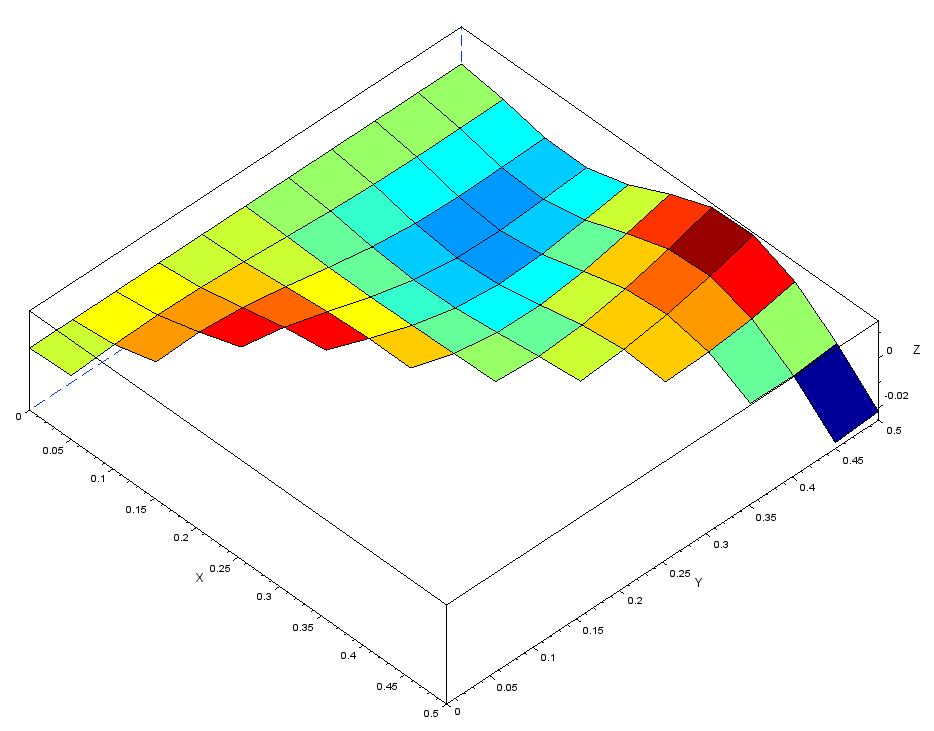

4.変形量と応力
薄板三角形の変形量及び応力の理論式を以下に示します。
尚荷重は0.1N(10gf)を端部50mmに均一に印加しました。
・変形量
δmax = P*L3/(2EI) = 16.8mm(面積モーメント法より導出)
P=9.807/100N L=0.5m E=70GPa I=bt3/12=0.5*0.00053/12
・応力
σxx = P*L*(t/2)/I = 2.35Mpa
P=9.807/100N L=0.5m t=.5mm I=bt3/12=0.5*0.00053/12
メッシュ別の変形量及び応力の解析結果を以下に示します。
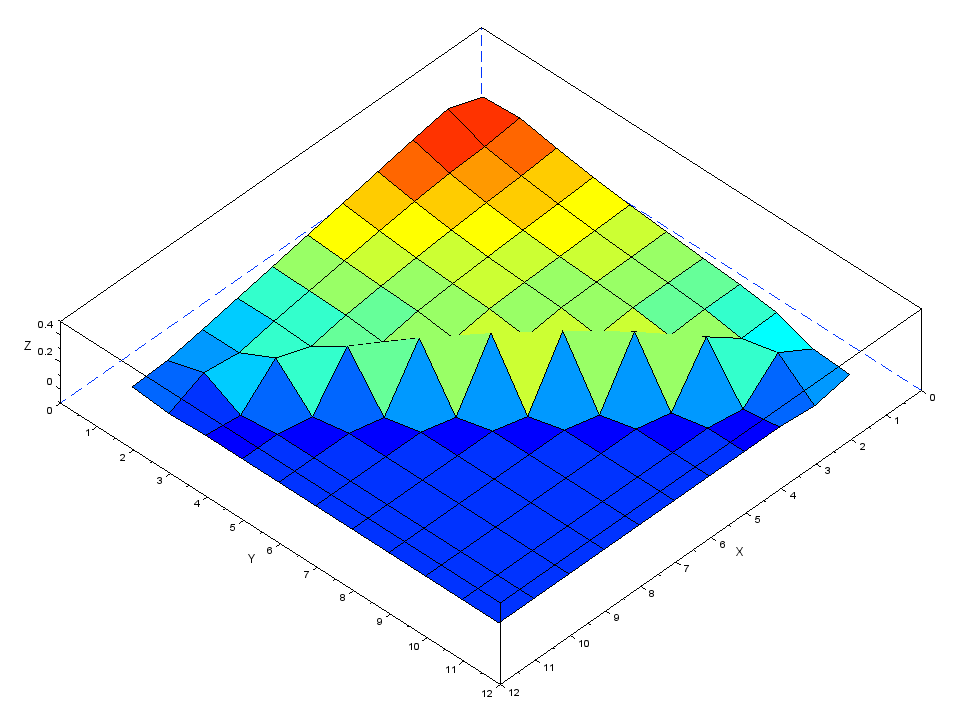
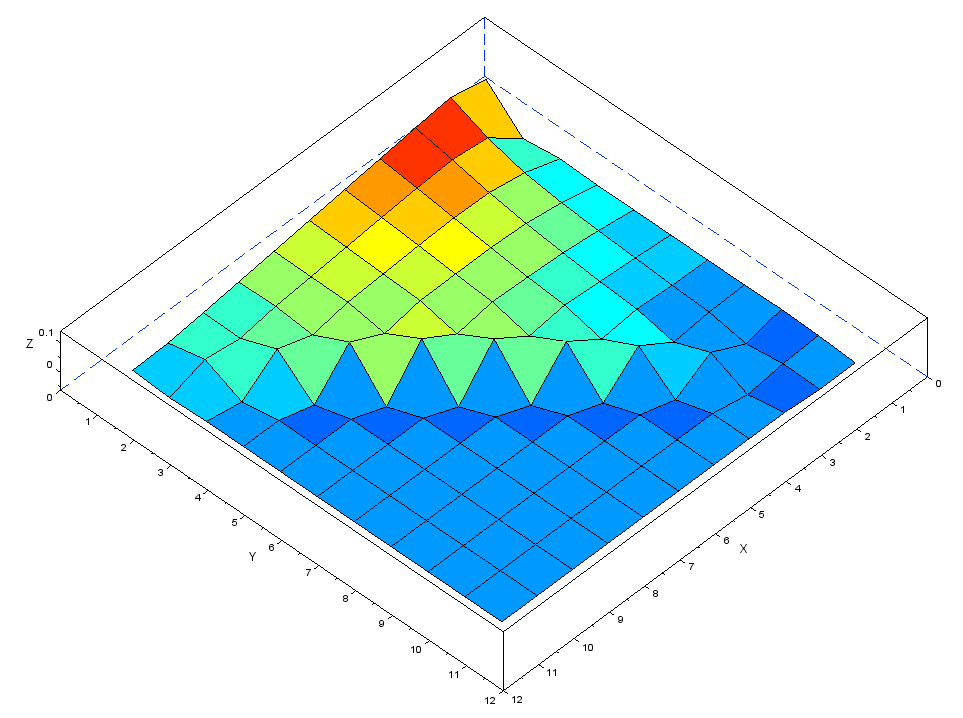
・メッシュ1 変位:δ=18.9mm理論値よりも変形量が少し大きくなっています。これは次に示す応力分布が均一でないためと考えられます。

・メッシュ1 応力:σxx=3.87Mpa、σyy=1.31Mpa、σvm=3.87Mpa、σmax=4.35Mpa
理論式は三角形の底辺に均一に曲げ荷重が分配された場合の値なのですが、三角形の場合曲げ荷重は均一にはならず、底辺の半分くらいで荷重を受けています。このため発生する応力も2倍程度になってしまうようです。この影響で前述の変形量も理論値よりも大きくなったと考えられます。
尚三角形をメッシュで模擬する際、斜辺が凸凹になってしまい、応力も不自然な形になってしまっています。
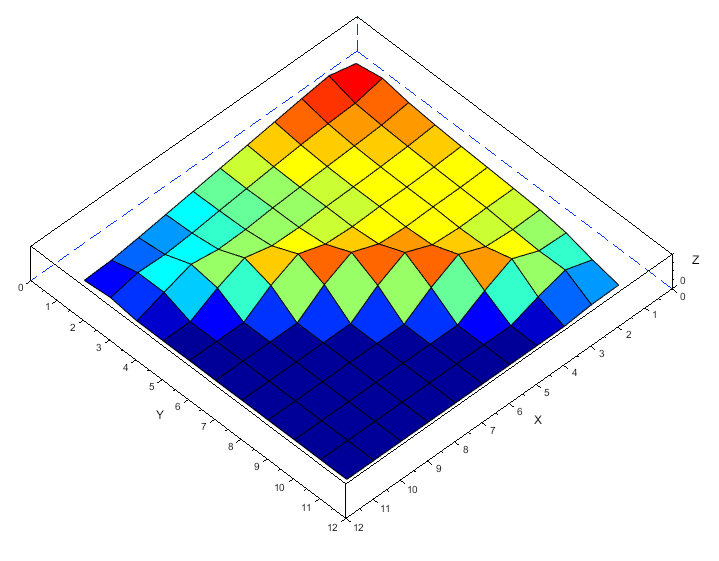
・メッシュ4.2 変位:δ=19.38mm
変位量はScilabとFreeCADはおおよそ一致しています。

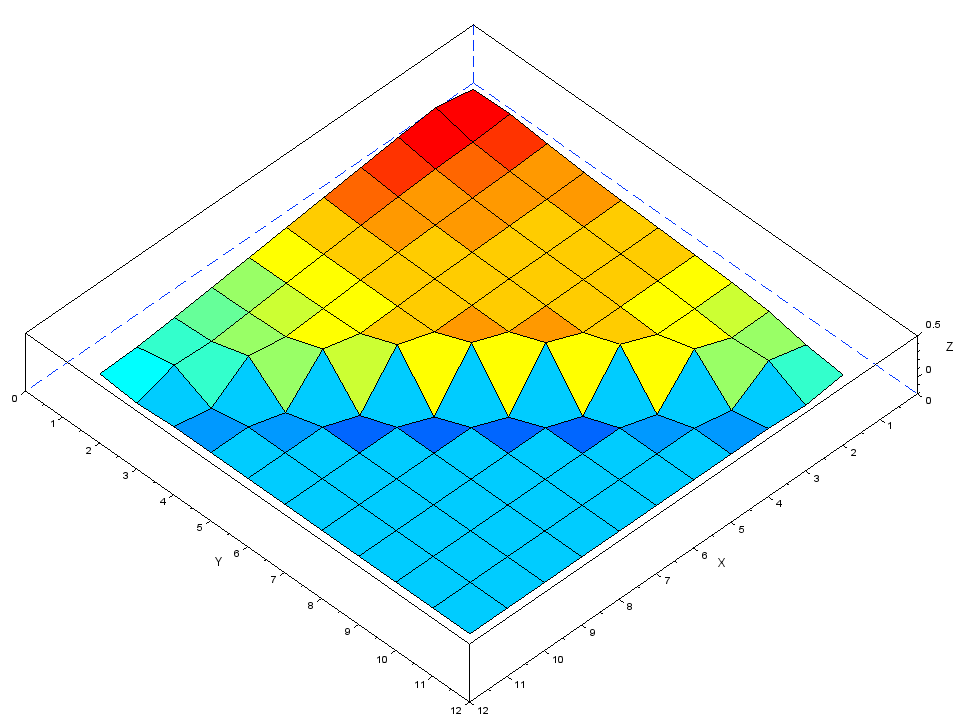
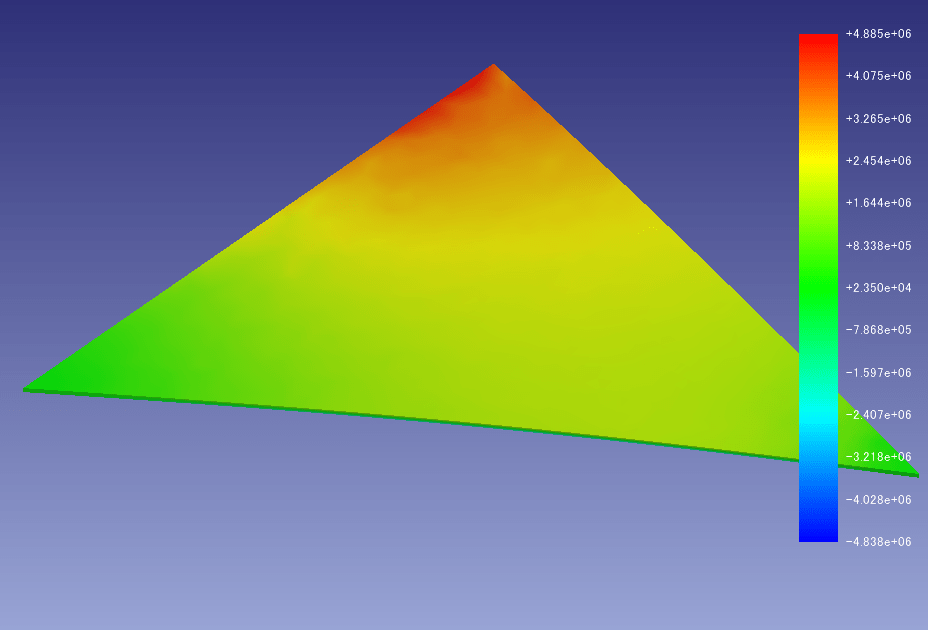
・メッシュ4.3 応力:σxx=4.89 Mpa、σyy=2.07Mpa、σvm=3.64Mpa、σmax=4.90Mpa
FreeCADでは斜辺が応力をよく伝えているようで、σyyがそれなりの大きさを示しています。
またσxxは四角形と比べると応力が三角形全体に広がっています。
これは断面2次モーメントが先端に行くに従い小さくなるからで理屈にあっています。
一方σvmとσmaxはScialabと大体一致しています。



全般的にScialbとFreeCADの解析結果がおおよそ一致することが確認出来ましたが、以下の注意が必要と考えます。
・Scialabの四角要素で三角形を解析する際は、斜辺の働きが十分模擬されていない。
・このため局所的な応力の向きが現実と違う恐れはある。
step3にてこのScilab解析を改善してみました。
step1に戻る
