「テーマ」
・公式の見当たらない薄板三角形1辺固定の固有振動数解析と強度解析を行う。
「方針」
Step1:公式のある薄板四角形をScilabおよびFreeCADで解析し、妥当性を確認する。
Step2:上記妥当性を基に薄板三角形の固有振動数と強度解析をScilabおよびFreeCADで実施する。
Step3:三角形要素を用いた強度解析を実施する。
「Step1:薄板四角形の解析」
1.モデル
検討対象は他解析と共通とするため以下で統一しました。
・500x500x0.5mmのアルミ板
・1辺のみ固定
2.メッシュ種類
以下の4種類を実施しました。
・メッシュ1:Scilab 10×10マス
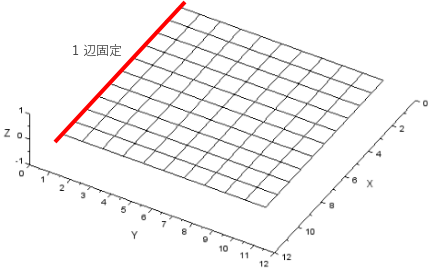
当事業所では動的解析はScilabでしか実施出来ないため、
Scilabの精度を確認する必要があります。
・メッシュ2:Gmesh(FreeCAD装備)

緻密なモデル作成用メッシャー。
非均一なメッシュとなっています。
今回の設定は
[要素の次数=2nd / 最大要素30mm / 最小要素0.1mm]
・メッシュ3:Netgen(FreeCAD装備)

手軽なモデル作成用メッシャー 。
規則性のあるメッシュとなっています。
今回の設定は[最大要素30mm / 中程度の粗さ]
・メッシュ4:Gmesh(FreeCAD装備)

Gmesh、Netgen共にそもそも薄板はメッシュ厚さの
観点から難しい解析のようです。
そこで板厚を敢えて10倍の5mmとし、以下の修正で
疑似的に等価な解析を実施してみました。
・メッシュ4.1:固有値解析:密度を100倍に修正。
・メッシュ4.2:変形量解析:荷重を1000倍に修正。
・メッシュ4.3:応力解析 :荷重を100倍に修正。
3.固有値解析
薄板四角形の固有値の理論式(参考文献[1])を以下に示します。
f=(1/2π)・(λ2/a2)・√(D/ρt)
D=Et3/(12(1-ν2))
λ2=3.494(1次)、8.547(2次)、21.44(3次)、27.46(4次)、31.17(5次)
a:板の1辺の長さ[0.5m]
D:曲げ剛性[E=7*1010Pa][ν=0.3]
ρ:密度[2800kg/m3]
t:板厚[0.5mm]
メッシュ別の固有値解析の結果(1~5次モード)を以下に示します。
・1次モード(理論値1.68Hz)
メッシュ1=1.67Hz、メッシュ2=1.69Hz、メッシュ3=1.83Hz、メッシュ4.1=1.68Hz



・2次モード(理論値4.12Hz)
メッシュ1=4.10Hz、メッシュ2=4.33Hz、メッシュ3=4.92Hz、メッシュ4.1=4.12Hz



・3次モード(理論値10.33Hz)
メッシュ1=10.27Hz、メッシュ2=10.86Hz、メッシュ3=12.61Hz、メッシュ4.1=10.34Hz

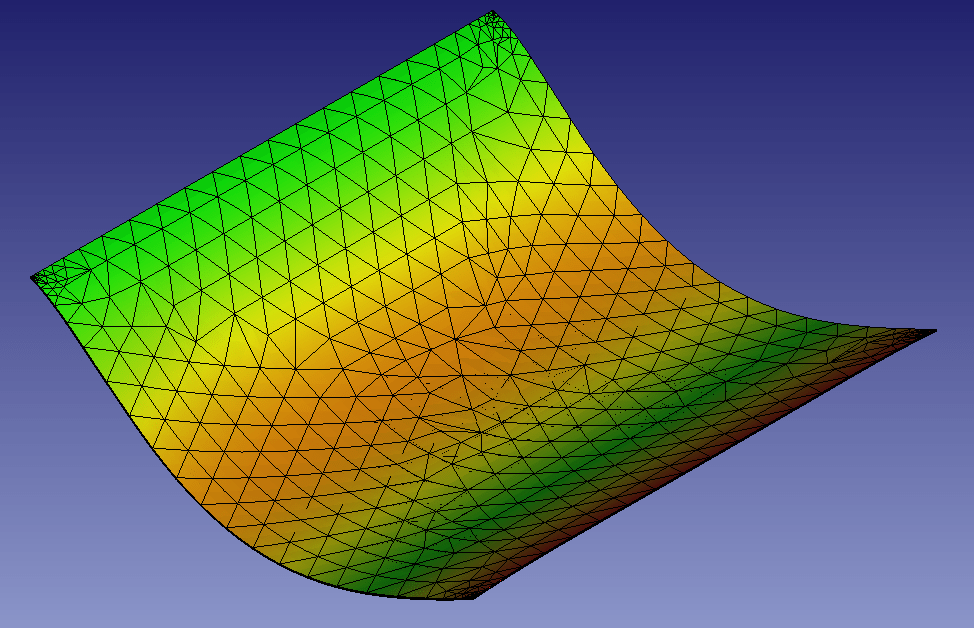

・4次モード(理論値13.23Hz)
メッシュ1=13.08Hz、メッシュ2=13.75Hz、メッシュ3=27.85Hz、メッシュ4.1=13.15Hz
(メッシュ3は精度が悪すぎるようです)
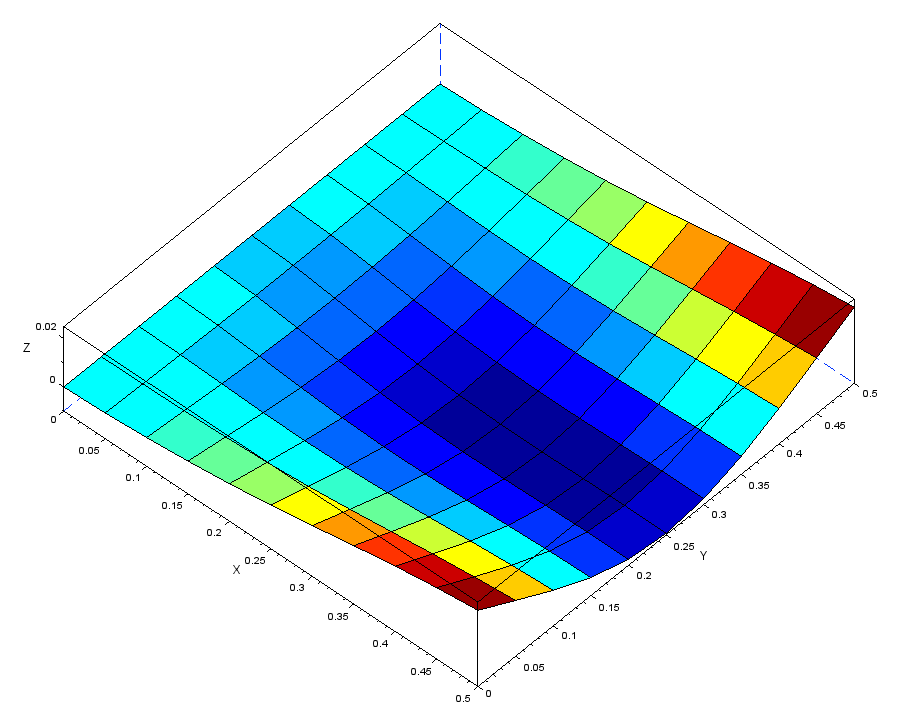

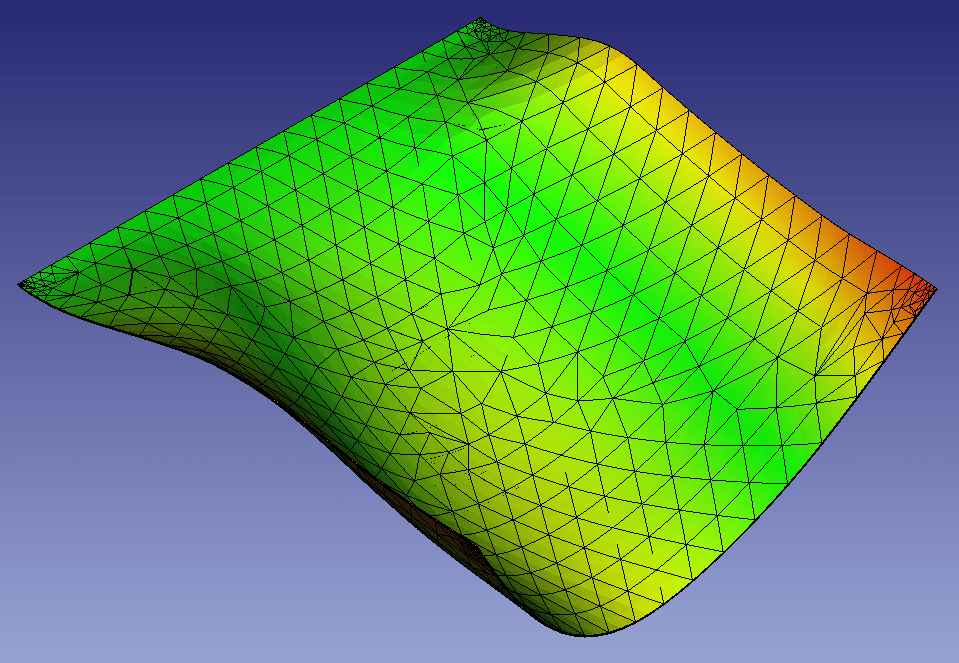
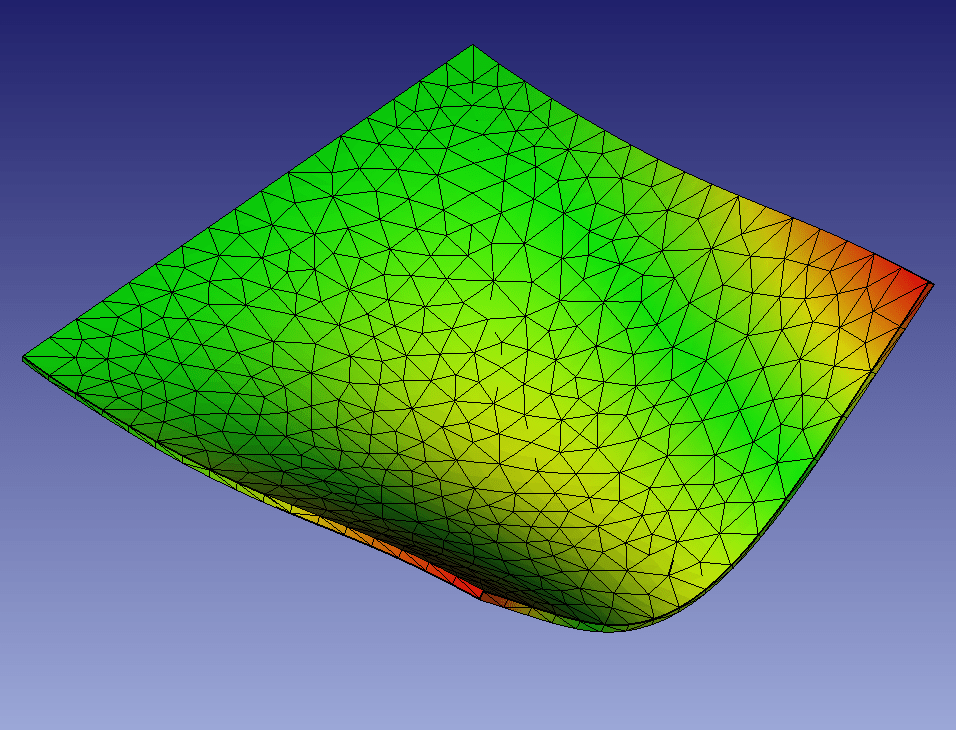
・5次モード(理論値15.01Hz)
メッシュ1=14.91Hz、メッシュ2=16.32Hz、メッシュ3=42.01Hz、メッシュ4.1=15.04Hz
(こちらのメッシュ3も精度が悪すぎるようです)
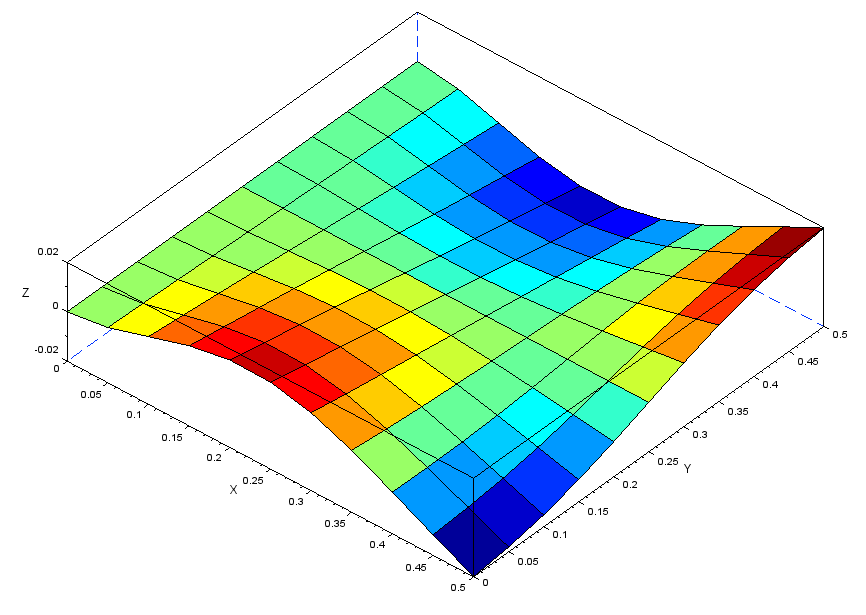

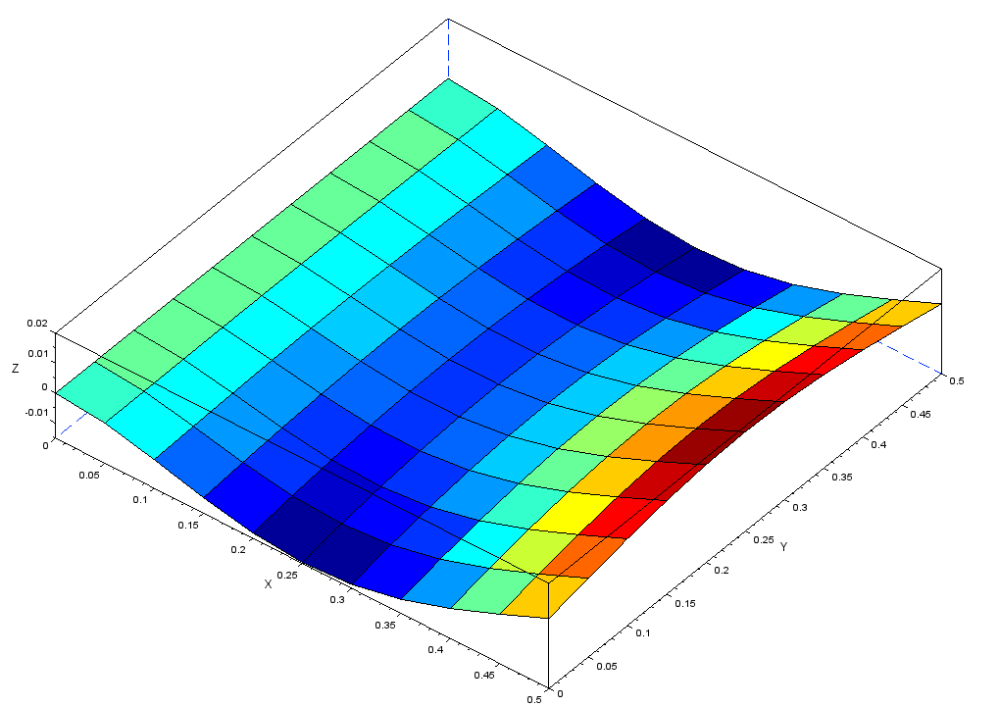
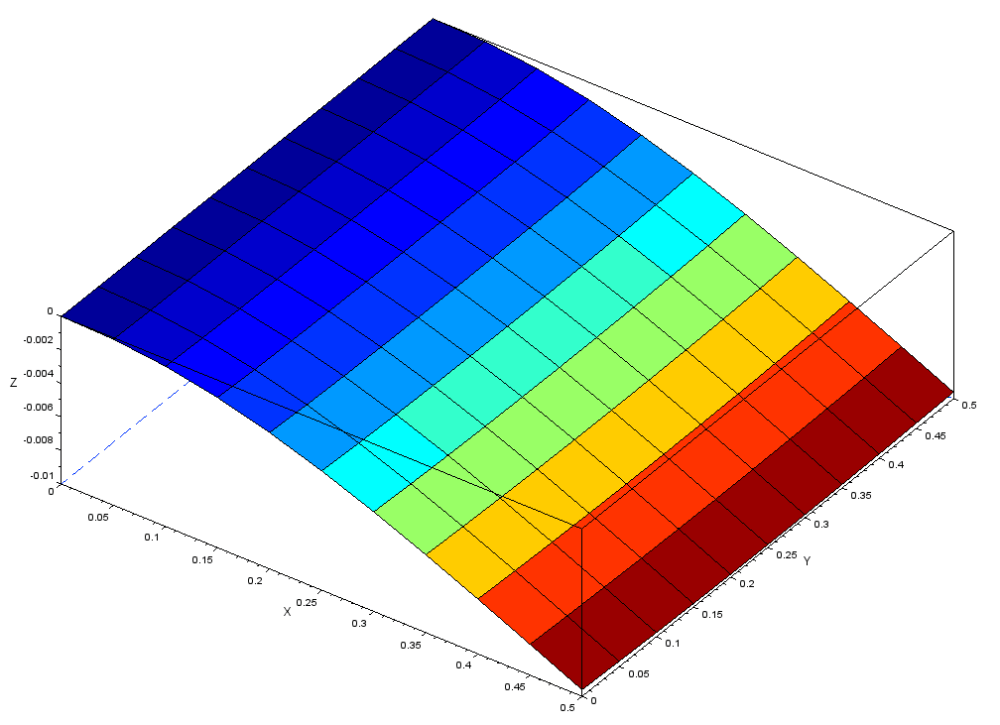
4.変形量と応力
薄板四角形の変形量及び応力の理論式を以下に示します。
尚荷重は0.1N(10gf)で固定辺と反対の縁50mmに印加しました。
・変形量
δmax = P*L3/(3EI) = 11.2mm
P=9.807/100N L=0.5m E=70GPa I=bt3/12=0.5*0.00053/12
・応力
σxx = P*L*(t/2)/I = 2.35Mpa
P=9.807/100N L=0.5m t=.5mm I=bt3/12=0.5*0.00053/12
メッシュ別の変形量及び応力の解析結果を以下に示します(数値のみ)。
理論値 :δ=11.2mm、 σxx=2.35Mpa
・メッシュ1 :δ=9.8mm、 σxx=2.45Mpa、 σvm=2.18Mpa、 σmax=2.45Mpa
・メッシュ2 :δ=8.66mm、 σxx=1.81Mpa、 σvm=1.60Mpa、 σmax=1.81Mpa
・メッシュ3 :δ=9.26mm、 σxx=2.95Mpa、 σvm=2.13Mpa、 σmax=2.95Mpa
・メッシュ4.2:δ=9.73mm、 σxx=27.35 Mpa、σvm=20.20Mpa、σmax=27.36Mpa
・メッシュ4.3:δ=0.97mm、 σxx=2.73 Mpa、 σvm=2.02Mpa、 σmax=2.73Mpa
注:σvm フォンミーゼス応力、σmax 最大主応力

5.総合評価
前項までの計算結果を下表にまとめます(◎、〇、△、×は相対評価)。
表よりおおよそ以下が言えると考えます。
・メッシュ4(Gmesh、厚さ5mm)が最も信頼性が高そう。
・メッシュ3(Netgen)は固有値の高モードで理論値からかけ離れている(薄板に弱い模様)。
・メッシュ2(Gmesh)はScilabに劣る(薄板に弱い模様)。
・メッシュ1(Scilab)はメッシュ粗さの割に健闘している。
以上から静的解析はGmeshの厚みを増やすことで十分信用出来る解析結果が得られると考えます。
またScilabも理論値と十分一致しており、動的解析の使用にラフな精度ならば耐えられると考えます。
| 解析種類 | 固有振動数f1 | 変形量δ | 最大主応力σmax | |||
| 理論値 | 1.68Hz | – | 11.2mm | – | 2.35Mpa | – |
| Scilab 11×11 | 1.67Hz | ◎ | 9.8mm | 〇 | 2.45Mpa | 〇 |
| Gmesh 30-0.1mm | 1.69Hz | ◎ | 8.83mm | △ | 1.84Mpa | △ |
| Netgen 30mm | 1.83Hz | × | 9.26mm | 〇 | 2.95Mpa | 〇 |
| Gmesh 30mm(厚さ5mm) | 1.68Hz | ◎ | 9.73mm | 〇 | 2.73Mpa | 〇 |
本結果をもとにstep2では薄板三角形の解析を行ってみます。
参考文献
[1]機械振動学 岩田佳雄・佐伯暢人・小松崎俊彦 共著 数理工学社
