「テーマ」
・ScilabとOpenFoamを用いてフラッタ解析を行う。
「方針」
一般論としてフラッタ解析は構造解析と流体解析を同時に行う必要があり、対応する解析ソフトウエアは高価となります。対してここではフリーソフトウェアであるScilabとOpenFoamを用いてフラッタ解析に挑戦してみようと思います。フラッタ現象を以下の当事業所オリジナル・モデルに落とし込むことでトライしてみます。
・フラッタ現象の中で最も代表的なものである1次曲げと1次捩りの連成を扱う。
・OpenFoamにより代表的な形状(通常形状と1次捩り形状)の空気力を事前に計算する。
・Scilabにより薄板の動的挙動を計算する。その際OpenFoamにより取得した空気力を外力として取り込む。
1.解析設定
検討対象は適当に以下の状況としました。
・200x400x0.5mmのアルミ板
・片端のみ固定
・迎角2°

2.解析手段
2.1 Scilab
以下のモデルで薄板を解析します。
・50×50mmの正方形マスで5x9の節点

2.2 OpenFoam
以下のモデルで薄板に働く空気力(通常形状と1次捩り形状)を計算します。
・200x400x5mmの薄板(メッシュ粗さから板厚0.5mmを5mmに変更)
・空間2(長さ) x 1(高さ) x1(幅)mを40x20x20の合計16000マスに分割(1マス50mm立方)
・薄板近辺のメッシュ粗さは上記1マスを1/16に緻密化(1マス3mm立方)

3.解析
3.1 モデル概要
フラッタ解析に使用するScilabモデルを以下に示します。フラッタ計算としては非常に簡単なモデルとなっています。

モデルの構成は以下となります(詳細を5項に示します)。
・薄板構造部
薄板の剛性行列[Kf]と質量行列の逆行列[MIf]により構成されており、本モデルの積分部分となります。
・通常外力(空気力)
通常形状(変形していない状態)での空気力[Ini_forceU1]をここで印加します。
・1次捩り空気力
捩り運動による振動をモデル化します。具体的には1次捩りの形状により発生する空気力をOpenFoamにて事前計算し、[Air_Mode119]として印加します。この空気力は薄板をより変形する側に働くため、剛性行列[Kf]を弱めることとなり固有振動数を下げる役割を担います。
尚これ自身は単なる振動源であり、発散の主原因とはなりません。
・1次曲げダンピング力
曲げ運動による局所速度変化は周囲速度との合成により迎角を減少させる方向に働きます。
具体的にはScilabモデル上での①~⑤の列を1組として、組毎(9組)にその面直方向運動と周囲速度から合成される迎角により発生する空気力の増減分を通常形状から推算し、[Air120_AOA]として印加します。
尚このダンピング力が発散の主たる原因(ばね系での自励振動の例)となります。
4.計算結果と考察
Scialbの計算結果は以下の形状が時間毎に得られます。
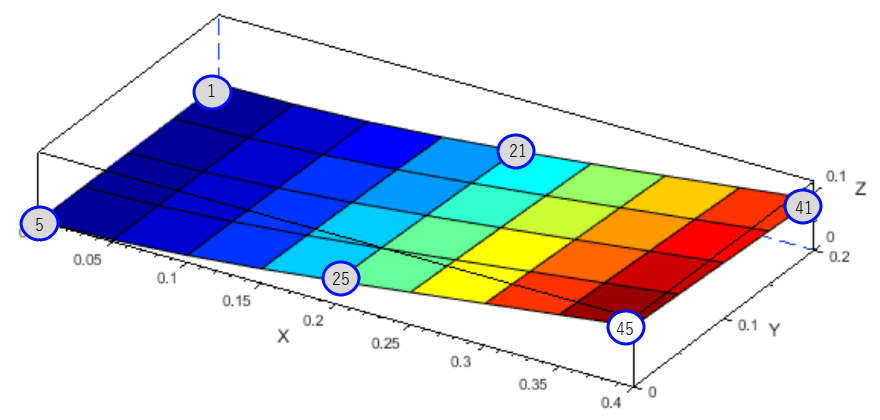
可視化するため点45の面直運動の値をグラフにしました。
また1次曲げ変形量と1次捩り変形量の様子を確認するためScilabモデル中の<Mode119>と<Mode120>での変数の様子もグラフにしました。(格子数45点に対し端部固定のため、自由度は40点×3で120となり
Mode(基底)も120個となります。今回のScilab計算ではMode120が1次曲げ変形、Mode119が1次捩り変形に対応していました)。
結果が以下となります(風速5、12、13m/sを示します)。


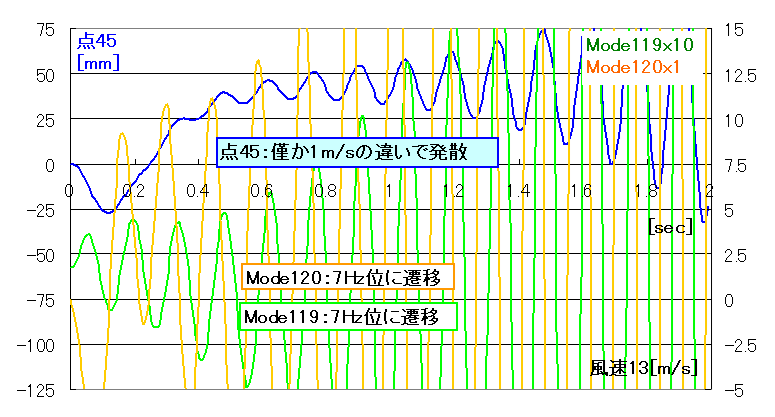
グラフより以下が確認出来ました。
・微風5[m/s]では1次曲げ(Mode120)は本来の固有値2.6Hzに、1次捩り(Mode119)も本来の固有値11Hzに従った減衰を示している。
・風速12[m/s]では1次曲げと1次捩りが共に7Hz程度に遷移してきている。但し運動は収束した。
・風速13[m/s]では1次曲げと1次捩りが共に7Hz程度となり、運動が発散。僅か1[m/s]の違いで大きな違いとなった。
・一連の動きは文献(参考文献[1]9.5.2章)で示されている1次曲げと1次捩りによるフラッタの様相と定性的に一致する。
(7Hzは三角関数の和積公式に従い、1次曲げ2.6Hzと1次捩り11Hzの平均となっているのだと考えます。)
参考にシミュレーション時間1.94秒から10msec毎の外形変化の様子を6枚示しておきます。
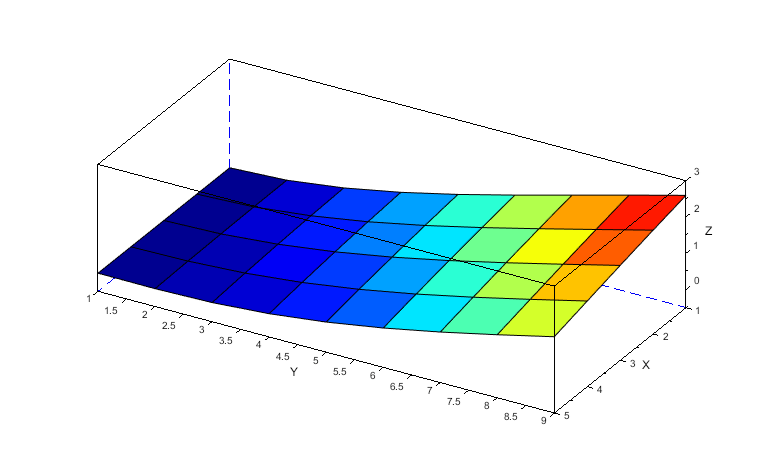
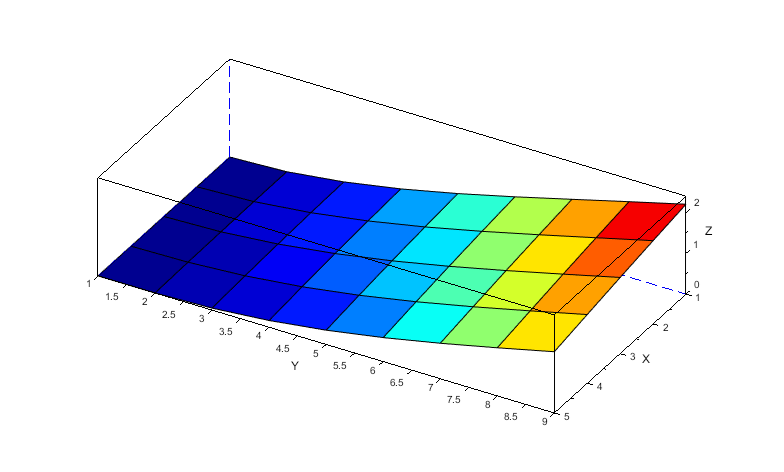


以上より本検討にて作成したScilabモデルは十分フラッタを模擬出来ていると考えます。
今一度本モデルの特徴を示します。
・本来同時に計算すべき構造解析と流体解析を別々に計算します。この際、流体解析は代表モード(1次曲げと1次捩り)の定常状態のみ解析し、その計算した空気力が構造変形に線形寄与するという大きな仮定をおいています。
・構造変形に対し空気力は一定の遅れを示すと考えられます。本モデルではその遅れを一定の1次遅れと仮定(5章)しました。
・フラッタは内部構造による減衰力に強く依存します。本モデルでは一つの構造減衰力で代表(5章)しました。
この特徴を受けて、以下の注意点が解析時に分かっています。
「注意点」
・空気力に設定した1次遅れの値にフラッタ解析結果が敏感になっています。
・内部構造減衰力にフラッタ解析結果が敏感です。
本モデルには上記注意点があり更にモデルそのものが当事業所オリジナルのため、実際の問題に適用する場合は実際の試験結果との比較検討が重要となります。
5.解析詳細
5.1 薄板Mode解析
以下の薄板のScilab変位法を用いたMode解析結果を示します。
・200x400x0.5mmアルミ板
・ヤング率70MPa / 密度2800kg/m3 / ポアソン比0.3
・5x9節点(50mm四方正方形)で1点辺りの自由度3(ω、ωx、ωy):変数定義はこちら
・端部固定により自由度は5点減って、全自由度は5x8x3=120。よってMode数も120。

Mode解析の結果は以下となりました。



このModeのうち、最も低次である1次曲げモードと1次捩りモードを以後のScilabモデルの対象とします。
5.2 動的解析モデル
前項を受けて動的解析用に以下のscilabモデルを作成しました。

(1)薄板構造部
5.1項で求めた以下の行列を元に積分部位を構成します。
・剛性行列[Kf]
・質量行列[Mf]の逆行列[MIf]
・減衰係数1%(構造減衰率2%)とした減衰項2*.01*[KMsqrt](詳しくはこちら)
この減衰係数は薄板内部構造に依存しており、試験値及び経験値との比較が重要となります。
(2)定常外力
初期状態の定常外力の条件を以下としました。
・200x400x5mm板(メッシュサイズから0.5mmを5mmに変更)
・迎角2°
・周囲速度2[m/s]
この条件のもと、OpenFoamを用いて薄板の上下面に働く圧力を計算しました。
OpenFoam設定
・空間2(長さ) x 1(高さ) x1(幅)mを40x20x20の合計16000マスに分割(1マス50mm立方)
・薄板近辺のメッシュ粗さは上記1マスを1/16に緻密化(1マス3mm立方)
・入口速度2m/s、出口は内部計算値、薄板表面及び薄板を取付た壁は表面速度0、それ以外の面はslip条件
・出口圧力0、その他はzeroGradien条件
・空気動粘性:2.0e-5 m2/s
・解析ソルバーはpisoFoam(非圧縮・非定常乱流解析ソルバー)
・乱流モデルはRAS(レイノルズ平均に基づく乱流モデル)でkEpsilonモデル(標準k-εモデル)
・epsilon、kは初期値0.1、nutの初期値は0(適当)。
上記以外のパラメータは以下のOpenFoamチュートリアルの物をそのまま使用しました。
tutorials\incompressible\pisoFoam\RAS\cavity

計算結果をparaviewのsave dataコマンドでCSVに吐き出し、45点に対応した点の表面と裏面の圧力差分を行列[Ini_force]とします。この計算では周囲速度U0を2[m/s]としたので、周囲速度U1の時は動圧補正を行い行列[ini_forceU1]=[Ini_force]x(U1/U0)2を定常外力としました。
尚薄板の縁は圧力変化が急なので6mm内側にオフセットした圧力を読み取ることとしました。
またScilab計算上、急激な入力による計算発散を防ぐため200msecのランプ入力としています(モデル上ランプ・ブロック)。
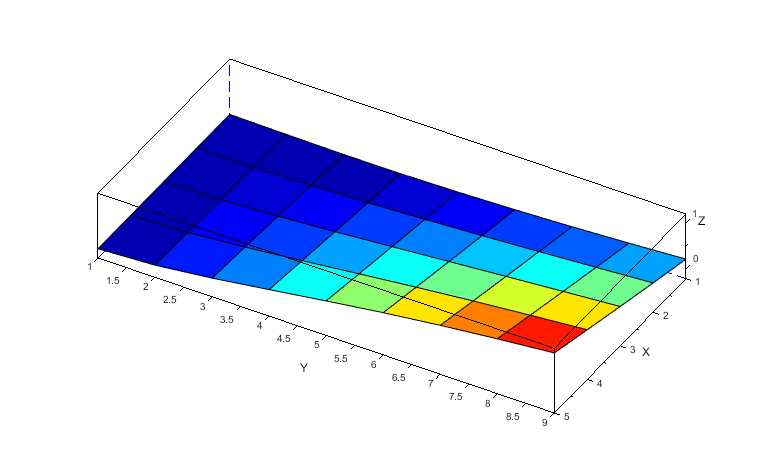
[Ini_force]の様子(U0=2[m/s])を以下に示します(縦横比適当)。揚力のほとんどを前縁が担っています。

ここで定義した定常外力に対する変形量を上述Scilabモデルで計算します。
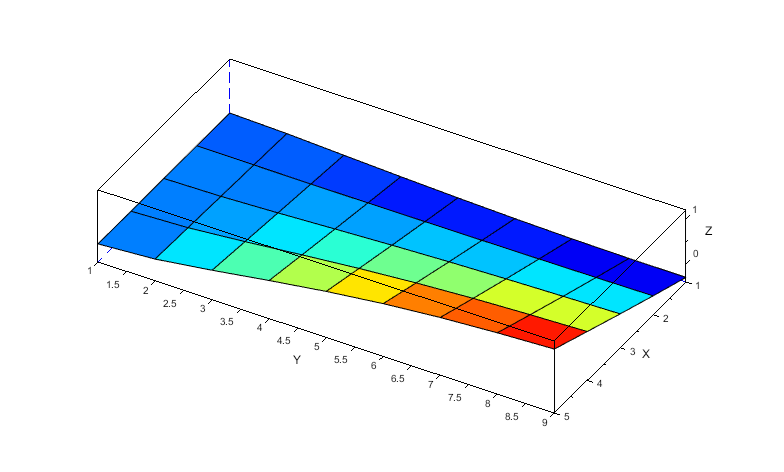
結果は以下で、端部で1.1mm浮き上がっています(下図は変位を拡大して表示しています)。
この計算結果の行列を[Ini_deflection]としておきます。こちらにも速度補正を加えておきます。
[Ini_deflectionU1]=[Ini_deflection]x(U1/U0)2
この変形量は次の項で使用します。

(3)1次捩り空気力
(2)項で定義した定常外力に対し、追加で微小な1次捩りモード変形が起きた際の空気力増減をOpenFoamで計算します。
・Scilabで計算したMode119の薄板形状を5mm厚にSolid化。
・迎角2°
・周囲速度2[m/s]
・OpenFoam設定は(2)項と同じ

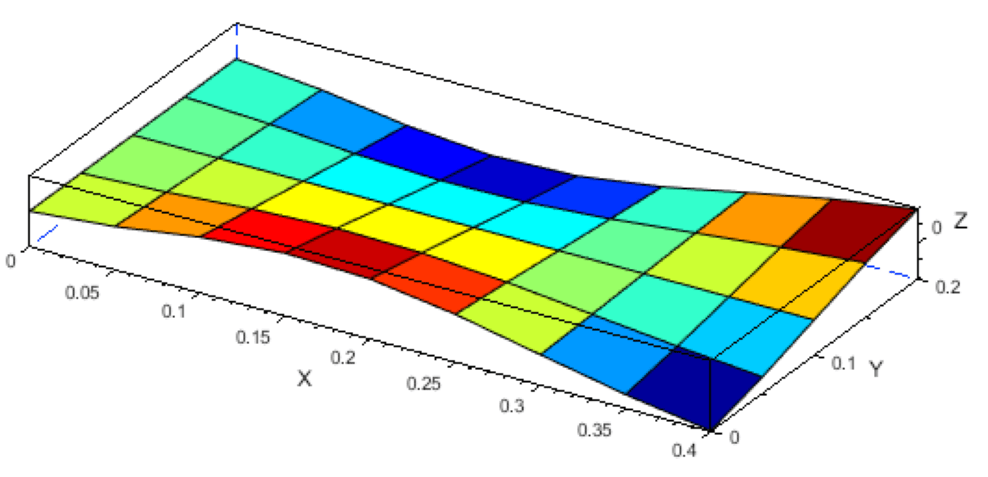
計算結果をparaviewのsave_dataコマンドでCSVに吐き出し、先ほどと同様に表面と裏面の圧力差分を求めます。更にその値から先ほどの行列[Ini_force]を引き算したものを行列[Air_Mode119]とします。この行列は迎角2°の薄板がMode119(1次捩り)の変形をした場合の空気力の増加分を意味します。[Air_Mode119]の様子を以下に示します(縦横比適当)。
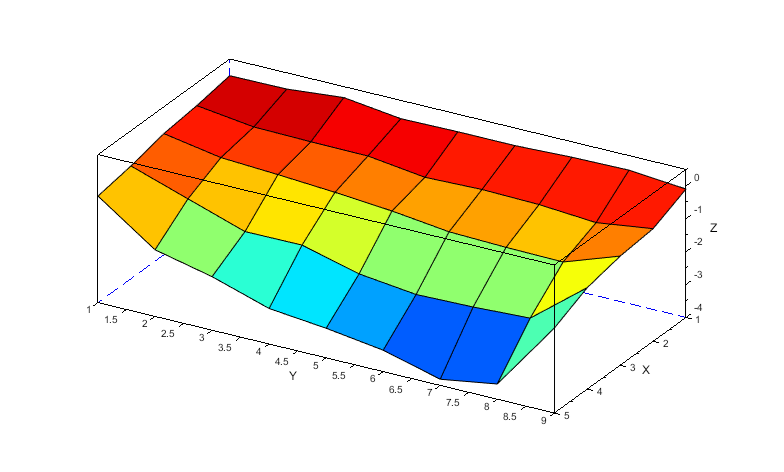
Mode119の形状はたまたま前縁下曲げとなっているため、負の揚力となっています。これ以降の計算ではモード成分がマイナスとなることで矛盾しないようになっています。
次にこの空気力増加分[Air_Mode119]をScilabモデルに取り込みます。
これ以降はScilab上のテクニックとなりますが、その目的は以下となります。
・薄板構造部で計算された外形変形量にMode119(1次捩り)がどの程度含まれているかを検出
・そのMode119の割合に合わせた空気力増加分[Air_Mode119]を薄板構造部にフィードバック
・このフィードバックは薄板の変形を増加する側となるため、「+」のフィードバック
(この「+」が薄板構造部の剛性行列[Kf]を弱める方向のため、4項で示したMode119の固有振動数11Hzが連成時7Hz位に減ると考えられます。)

①[Geye]:単なる120x120の単位行列。Scilab上、変数の明確化のために設置。
②FAII:薄板構造部の固有ベクトル[FAI]の逆行列[FAI]-1を示している。外形変形量をFAIIに掛けるとMode変換される。
③SM119:120x1のゼロ行列のうち、119行のみ「1」とした行列。これを②にかけることでMode119の成分が抽出される。
④-def119:(2)定常外力で計算された[Ini_deflectionU1]のMode119成分がdef119。定常外力によって引き起こされた変形分を引くことで動的な変化分を抽出。
⑤時定数taoの1次遅れブロック:(5)項で後述
⑥(U1/U0)2:[Air_Mode119]の速度補正。U0=2[m/s]
⑦[Air_Mode119]:薄板がMode119(1次捩り)の変形をした場合の空気力の増加分
※4項計算結果の出力抽出点
(4)1次曲げダンピング力
(2)項で定義した定常外力に対し、1次曲げモードの速度変形が起きた際の空気力増減を下記方法で求めます。
・[Ini_force]を補正することで作成。補正は節点5x9=45個の列毎に実施
例として㊶~㊺列の計算を示します。
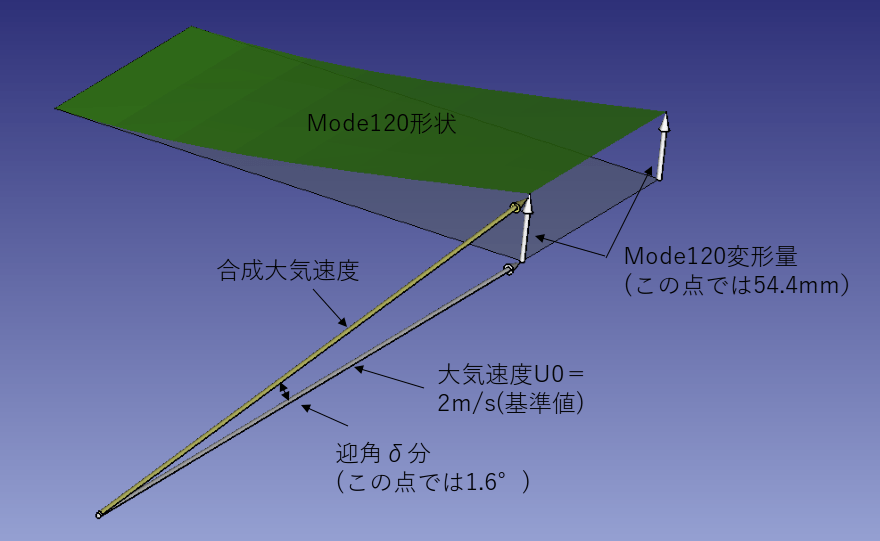
・Mode120の形状を単位時間(1秒間)に変形した量と仮定
・㊶~㊺列ではそれが54.4[mm]。
・周囲速度U0(2[m/s])と上記54.4[mm/s]薄板変形速度により局所的に迎角が変化。
・具体的には㊶~㊺列での迎角変化分=tan-1(54.4/2000)=1.6°
・[Ini_force]は迎角2°の揚力なので、[Ini_force]の㊶~㊺列の値を2°で割り、1.6倍したものを求めるべきダンピング力[Air120_AOA]とする。
尚薄板は気流に対して逃げていく方向に変形しているので迎角1.6°はもともとの迎角2°を減らす方向となります。
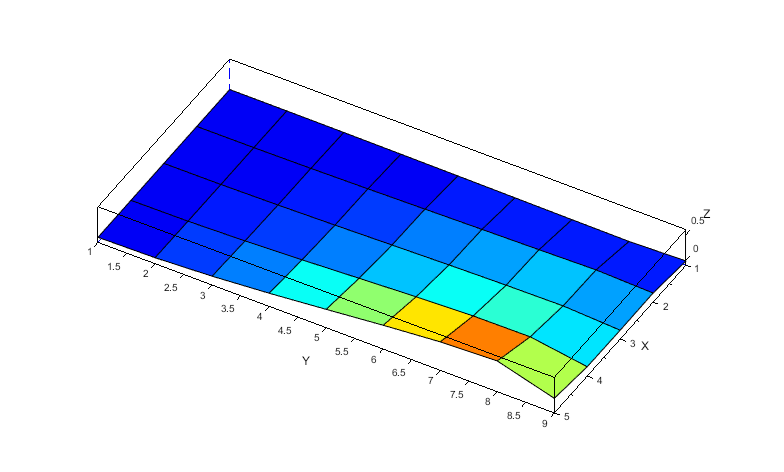
上記計算を各列毎に実施したダンピング行列[Air120_AOA]が以下となります(縦横比適当)。
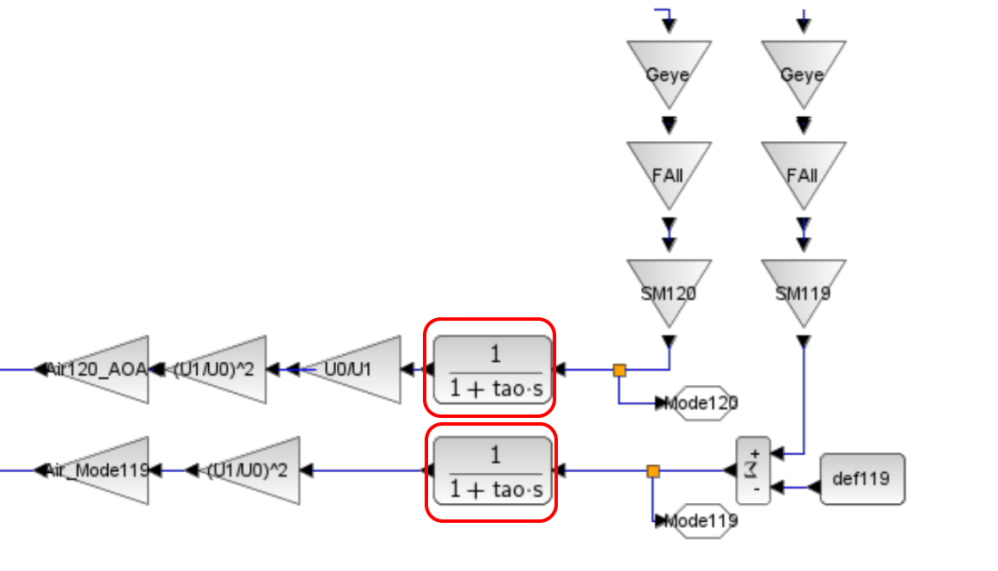
次にこのダンピング力[Air120_AOA]をScilabモデルに取り込みます。
これ以降はScilab上のテクニックとなりますが、その目的が以下となります。
・薄板構造部で計算された形状変更速度にMode120(1次曲げ)がどの程度含まれているかを検出
・そのMode120の割合に合わせたダンピング力[Air120_AOA]を薄板構造部にフィードバック
・このフィードバックは迎角を減らす側となるため、「-」のフィードバック (この項が発散の原因となるのは速度変化が増えると迎角が減るためです。簡単な例をこちらに示します)

①[Geye]:単なる120x120の単位行列。Scilab上、変数の明確化のために設置。
②FAII:薄板構造部の固有ベクトル[FAI]の逆行列[FAI]-1を示している。外形変形量をFAIIに掛けるとMode変換される。
③SM120:120x1のゼロ行列のうち、120行のみ「1」とした行列。これを②にかけることでMode120の成分が抽出される。
④時定数taoの1次遅れブロック:(5)項で後述
⑤(U0/U1):前進速度が変わることによる迎角補正。U0=2[m/s]
⑥(U1/U0)2:[Air120_AOA]の速度補正。U0=2[m/s]
⑦[Air120_AOA]:薄板がMode120(1次曲げ)の速度変形した場合のダンピング力
※4項計算結果の出力抽出点
(5)1次遅れ
本来薄板のフラッタ現象では構造変形に対し空気力変化が一定の遅れを持つことが重要と言われています。この点を1次遅れブロックによりの簡易に模擬しようと考えます。
[Ini_force]を計算したOpenFoamの計算では時定数taoは以下の感じとなりました。
tao = 薄板幅(0.2m)÷周囲速度(2[m/s]) x 0.5 (掛け数:適当)= 50[msec]
本Scilabモデルにおいては1次遅れtaoは上式周囲速度U0をU1に変更することのみで計算しました。
尚幾つかのフラッタ関連の論文で出てくるフラッタの速度パラメータは奇しくも上式と一致します。
但しここまで簡易な模擬なので実際の使用では掛け数0.5を0~1位で変化させ、解析結果がどれくらい振れるかを確認すべきと考えます。
6.補足解析
6.1 時定数パラメトリック・スタディ
参考として本文中注意点で記述した時定数の扱いに関し、掛け数を0~1に振った場合のフラッタ速度を確認してみました(減衰係数は1%保持)。この結果から掛け数の設定にある程度の目星が付けられます(0~1の確認で工学的に問題なさそうな感触が得られます)。
掛け数 フラッタ開始速度
0 7m/s
0.5 13m/s
1.0 14m/s

6.2 減衰係数パラメトリック・スタディ
参考として本文中注意点で記述した減衰係数の扱いに関し、減衰係数を0.10~100%に振った場合のフラッタ速度を確認してみました(1次遅れ時定数の掛け数は「0」とした)。この結果からも減衰係数の設定にある程度の目星が付けられます(0.1~100%の確認で工学的に問題なさそうな感触が得られます)。
減衰係数 フラッタ開始速度
0.1% 6m/s
1% 7m/s
10% 12m/s
100% 17m/s

6.3 初期迎角減衰係数パラメトリック・スタディ
参考として初期迎角2degを1deg~4degに振った場合のフラッタ速度を確認してみました(1次遅れ時定数の掛け数は「0.5」とした)。初期迎角が増減することは発散力に影響を与えるためフラッタ速度が変化しそうですが、計算結果からは不変でした。これは以下のためと考えています。
・例えは初期舵角を半分にしても、共振速度付近での速度に対する共振の増加率は遥かに大きいため、精度1m/s程度の計算ではフラッタ速度に違いが現れない。
初期迎角 フラッタ開始速度
1deg 13m/s
2deg 13m/s
4deg 13m/s
追記:計算時の条件(1degを例として示します)
・迎角1degでの空気力は迎角2degの値の半分とした。
・迎角1degでの変形量は迎角2degの値の半分とした。
・Mode119(1次捩り)の変形をした場合の空気力の増加分[Air_Mode119]は不変とした。
(計算時に初期舵角2degの影響を削除済み)
・Mode120(1次曲げ)の速度変形した場合のダンピング力[Air120_AOA]は不変とした。
(計算時に初期舵角2degの影響を削除済み)
・1次遅れ時定数も不変とした(適当)。

参考文献
[1]航空宇宙工学テキストシリーズ 空力弾性学 中道二郎 玉山雅人 児玉智 共著 丸善出版
