Detail1:変位法による薄板FEM解析詳細

「Detail1」変形法による薄板FEM

１.１　微小板要素の変形

　まず板の微小要素を考えていきます。

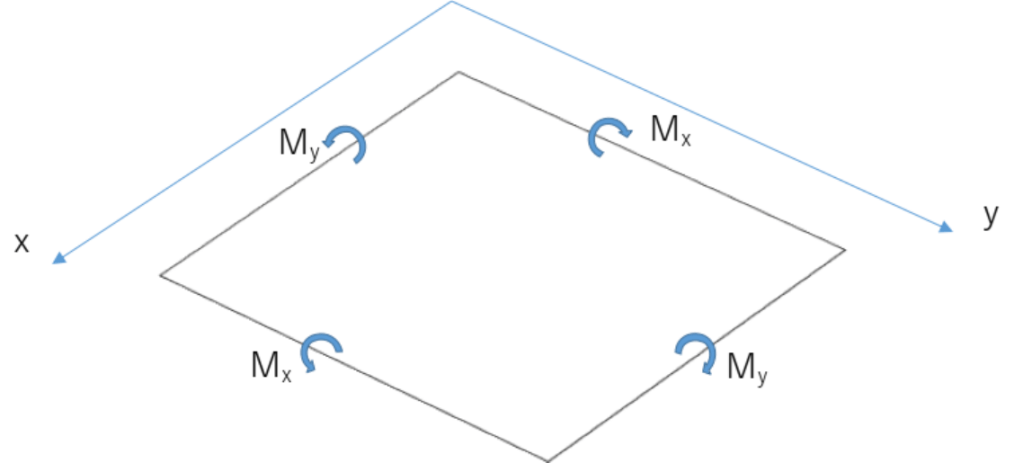
上図のようなモデルを考えた場合の薄板の曲げの基礎方程式は材料力学より以下となります。

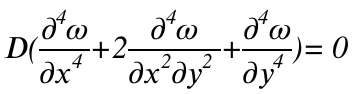
・・・(1)

・・・(2)

　　　　E : 板要素の縦弾性係数

　　　ｔ：板厚

　　　　ν：板要素のポアソン比

　　　　ω：板のz方向の変位

ここで微小板要素内部の変位ω_(x,y)を以下のようなxとyの関数で表現出来ると仮定します。ここでc₁～c₁₅は境界条件によって定まる定数で、境界条件と共に変化する定数です。

ω_(x,y)＝ c₁+c₂x+c₃y+c₄x²+c₅xy+c₆y²+c₇x³+c₈x²y+c₉xy²+c₁₀y³+c₁₁x³y+c₁₂xy³+c₁₃x⁴+c₁₄x²y²+c₁₅y⁴

（(1)式の形状より上記関数の次数は4次が上限になります）

しかし境界条件としては板要素端点のz方向変位、ｘ方向傾き、ｙ方向傾きから12の情報となり、この観点から15項を12項に絞ります(参考文献[1])。

ω_(x,y) ＝ c₁+c₂x+c₃y+c₄x²+c₅xy+c₆y²+c₇x³+c₈x²y+c₉xy²+c₁₀y³+c₁₁x³y+c₁₂xy³　・・・(3)

参考文献[1]に従い、具体的な計算を進めていきます。

変位の境界条件から上記変数ｃ₁～ｃ₁₂を計算するのですが、まず以下の準備を行います。

ω_(x,y)={N_(x,y)}{δ}　・・・(4)

{δ}={ω₁、ω_x1、ω_y1、ω₂、ω_x2、ω_y2、ω₃、ω_x3、ω_y3、ω₄、ω_x4、ω_y4}^T　：変位の境界条件

　但しω_x1=∂ω₁/∂x・・・etc

{N_(x,y)}：境界条件を入力とし、変位ω_(x,y)を出力します。以後変位関数と呼びます

(3)式より

∂ω_(x,y)/∂x = 0+c₂+0 +2c₄x+c₅y+0 +3c₇x²+2c₈xy+c₉y² +0 +3c₁₁x²y+c₁₂y³　・・・(5)

∂ω_(x,y)/∂y = 0+0+c₃ +0+c₅x+2c₆y +0 +c₈x²+2c₉xy +3c₁₀y²+c₁₁x³ +3c₁₂xy²　・・・(6)

例えば各点の(x,y)座標が点1(0,0)、点2(0,1)、点3(1,0)、点4(1,1)の場合、

(3)(5)(6)式にｘ、y座標の値を代入することで以下が得られます。

ω₁= c₁+0+0 +0+0+0 +0+0+0 +0+0+0

ω_x1=0+c₂+0 +0+0+0 +0+0+0 +0+0+0

ω_y1=0+0+c₃ +0+0+0 +0+0+0 +0+0+0

ω₂= c₁+0+c₃ +0+0+c₆ +0+0+0 +c₁₀+0+0

ω_x2=0+c₂+0 +0+c₅+0 +0+0+c₉ +0+0+c₁₂

ω_y2=0+0+c₃ +0+0+2c₆ +0+0+0 +3c₁₀+0+0

ω₃ =c₁+c₂+0 +c₄+0+0 +c₇+0+0 +0+0+0

ω_x3=0+c₂+0 +2c₄+0+0 +3c₇+0+0 +0+0+0

ω_y3=0+0+c₃ +0+c₅+0 +0+c₈+0 +0+c₁₁+0

ω₄ = c₁+c₂+c₃ +c₄+c₅+c₆ +c₇+c₈+c₉ +c₁₀+c₁₁+c₁₂

ω_x4= 0+c₂+0 +2c₄+c₅+0 +3c₇+2c₈+c₉ +0+3c₁₁+c₁₂

ω_y4= 0+0+c₃ +0+c₅+2c₆ +0+c₈+2c₉ +3c₁₀+c₁₁+3c₁₂

まとめますと

{δ}=[C]{c}

但し(編集ソフトウエアの都合、縦棒はカッコを示しています)

{δ}={ω₁、ω_x1、ω_y1、ω₂、ω_x2、ω_y2、ω₃、ω_x3、ω_y3、ω₄、ω_x4、ω_y4}^T

[C]=

{c}={c₀,c₁,c₂,c₃,c₄,c₅,c₆,c₇,c₈,c₉,c₁₀,c₁₁,c₁₂}^T ・・・(7)

(3)式と(7)式より

ω_(x,y) ＝{ 1 x y x² xy y² x³ x²y xy² y³ x³y xy³ }{c}

={ 1 x y x² xy y² x³ x²y xy² y³ x³y xy³ }[C]^-1{δ}

よって変位関数は以下となります。

{N_(x,y)}={ 1 x y x² xy y² x³ x²y xy² y³ x³y xy³ }[C]^-1 ・・・(8)

１．２　微小板要素の曲げモーメント

　材料力学より

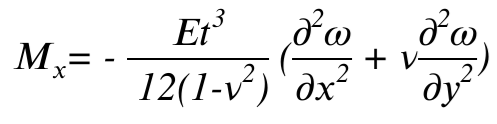
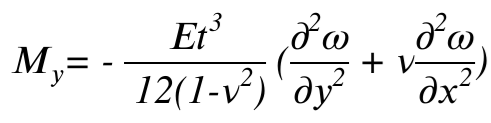
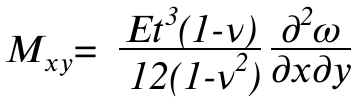
（M_xy:x平面上のy方向せん断力による曲げモーメント）

行列表示にします。　　　　　　

　　　　　=[D]*{ε}　　・・・(9)

{ε} = { -∂²ω/∂x²、-∂²ω/∂y²、2*∂²ω/∂x∂y}

上式を変位関数を用いて表現すると

-∂²ω/∂x²　= -2c₄-6c₇x-2c₈y-6c₁₁xy

-∂₂ω/∂y² = -2c₆-2c₉x-6c₁₀y-6c₁₂xy

2*∂₂ω/∂x∂y = c₅+4c₈x+4c₉y+6c₁₁x²+6c₁₂y²

行列で表現すると

{ε} = [Q]{c} ・・・(10)

[Q] =

・・・(11)

(7)式の逆行列により

{c}=[C]^-1{δ} ・・・(12)

(11)式を(9)式に代入すると

{ε} = [Q][C]^-1{δ}　・・・(13)

(13)式を(9)式に代入することで下記剛性行列(入力が変位δで出力が曲げモーメント)の形を作ることが出来ます。

すなわち

{Mx,My,Mxy}^T =[D]{ε}＝[D] [Q][C]^-1{δ} ・・・(14)

　ところがこの式には大きな問題があります。(14)式の左辺{M_x,M_y,M_xy}^Tと右辺の{ω,ω_x,ω_y}では扱っている座標の方向が違います。座標の方向が違っていては運動解析には使えません。

　そこで剛性行列の定義をやり直します。

すなわち微小板要素内での内部応力の行う仕事量を積分で算出し((15)式左辺積分)、それを代表点の変位{δ}で割ることで{δ}に対応した荷重、曲げモーメントを算出します。ここまでは厳密な計算でしたが、ここからは変位点での平均的な荷重を求めるという大きな方針転換を行います。

　内部応力仕事量= 1/2*∫{ε}^T[σ]dv = 1/2*∫{δ}^T[C]^-T[Q]^T[D][Q][C]^-1{δ}dxdy　・・・(15)

　(dvのうち、dzは[D]の計算で先行して行われているためdxdyに変わっています)

　(1/2はひずみエネルギーの係数、[σ]={Mx,My,Mxy}^T)

(15)式を{δ}で割ったものが{δ}に対応した荷重{F_z,M_x,M_y}となります。

{F_z,M_x,M_y} = [C]^-T∫[Q]^T[D][Q]dxdy[C]^-1{δ}　・・・(16)

結果、剛性行列は以下となります。

[K] = [C]^-T∫[Q]^T[D] [Q]dxdy[C]^-1 ・・・(17)

　後述の質量行列[M]の定義も(15)(16)(17)式と同じとなります。変位関数により微小要素内での変位量と慣性力を定義し、微小要素体積内で積分します。それを節点変位の2次微分で割ることで疑似的な質量を定義しています。よって質量行列は微小要素全体での慣性力を節点変位を変数に置き換えた場合の仮想質量と考えることが出来ると思います。

２．１　1要素板の計算

　ここで下図のようなモデルの具体的な計算例を示します。

E：ヤング率　　　7e10[Pa]

ρ：密度　　2800[kg/m3]　　　　　　　　

Ｌ：要素の縦長さ 1[m]　　　　　　　　・・・(18)

ｔ：厚さ　　　　　10[mm]

ν：ポアソン比　　0.3

　　節点座標：P₁=(0,1)、P₂=(0,0)、P₃=(1,1)、P₄=(1,0)

要素１(図左側の正方形)について[K]と[M]を求めていきます。

(7)式の計算により(但し節点の順番が変わっています)

[C] =

続いて(17)式の積分の中を計算していきます。

D₁＝Et³/(12(1-ν²))として

[D][Q]=D₁*

・・・(19)

更に[Q]^Tを加えると

[Q]^T[D] [Q]＝D₁*

・・・(20)

(20)式を要素１の面積で積分します。

尚積分範囲はx=0～1、y=0～1となり、且つxとyは独立変数であるため積分は容易です。

(ν=0.3を代入します)

∫[Q]^T[D] [Q]dxdy＝D₁*

・・・(21)

(21)式を(17)式に代入すると要素１の剛性行列[K]となります。

尚本計算は手計算では厳しいため、Scilabを使っています。

[K] = [C]^-T[(21)式][C]^-1 =D₁*

・・・(22)

続いて質量行列[M]を求めていきます。

参考文献[1]の定義式より

[M]＝∫{N}^T{N}ρdv

=[C]^-T∫{1 x y x² xy y² x³ x²y xy² y³ x³y xy³}^T{1 x y x² xy y² x³ x²y xy² y³ x³y xy³}ρdxdydz[C]^-1

・・・(23)

まず積分の中身を計算します。

{1 x y x² xy y² x³ x²y xy² y³ x³y xy³}^T{1 x y x² xy y² x³ x²y xy² y³ x³y xy³} =

・・・(24)

(24)式を要素１の面積で積分します。

尚積分範囲はx=0～1、y=0～1となり、且つxとyは独立変数であるため積分は容易です。

∫{1 x y x² xy y² x³ x²y xy² y³ x³y xy³}^T{1 x y x² xy y² x³ x²y xy² y³ x³y xy³}dxdy=

・・・(25)

(25)式を[C]^-Tと[C]^-1で挟みます(この計算も手計算では厳しいのでScilabを用いました)。

[C]^-T[(25)式][C]^-1＝

・・・(26)

以上より質量行列[M]は以下となります。

[M] = ρt*

・・・(27)

剛性行列[K]と質量行列[M]が求められたので、単振動バネと同じように固有値が求められます。

　固有値計算の前に拘束条件を計算に含めます。

点1と点２を拘束するとします。そうすると境界条件として以下となります。

{ω₁、ω_x1、ω_y1、ω₁、ω_x1、ω_y1} = {0}　・・・(28)

この境界条件により[K][M]の１～６行、１～６列は計算する必要がなくなります(「0」で固定)。

この点を反映した剛性行列と質量行列を[Kf]、[Mf]とすると

[Kf]=D₁*

・・・(29)

[Mf]=ρt*

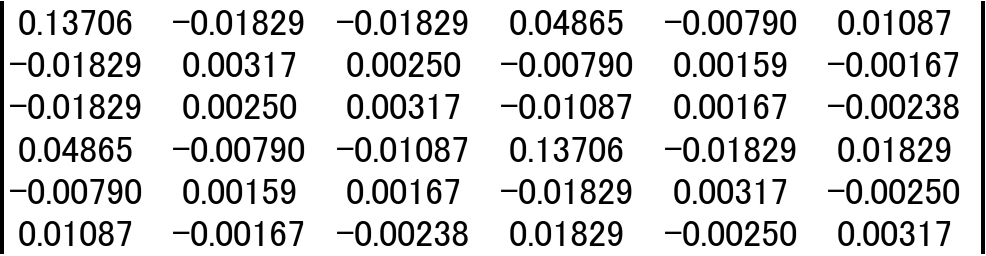
・・・(30)

SciabのコマンドKM=[M]^-1[K]、[P,D]=spec(KM)を用いて計算した結果を以下に示します。

・・・(31)

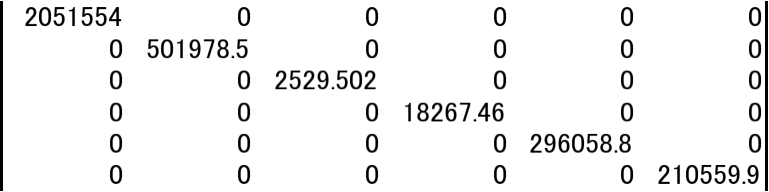
・・・(32)

D=ω²、ω=2πfより

・・・(33)

(33)式の確からしさを梁の理論式より確認します。

梁の固有振動数に関する理論式（参考文献[2]）

・・・(34)

固定-自由端　λ₁=1.875、λ₂=4.694、λ₃=7.855、λ₄=10.996

　∴ f₁=8.08Hz、f₂=50.62Hz、f₃=141.74Hz、f₄=277.76Hz　・・・(35)

(33)式の最小振動数f=8.00Hzは上記1次モードと十分一致しており、有限要素による解法の妥当性が示せたと考えます(さすがに１要素では２次モード以降は一致しないようです）。

２．２　4要素板の計算

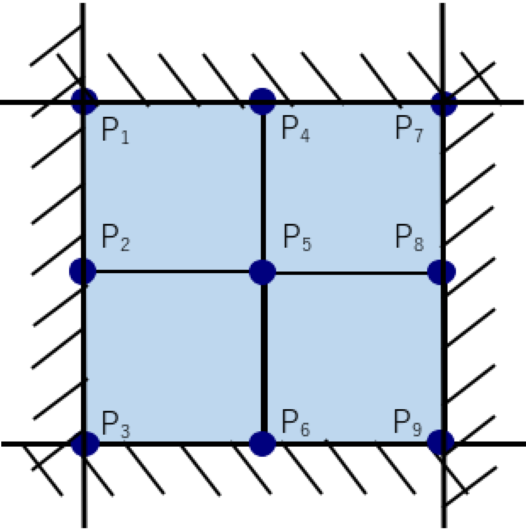
前項の１要素を４つに増やし、更に拘束を全周に施した下図のようなモデルの具体的な計算例を示していきます。

E：ヤング率　　　7e10[Pa]

ρ：密度　　2800[kg/m3]　　　　　　　　

Ｌ：要素の縦長さ 1[m](全体で2ｘ2ｍ)　　　　　・・・(36)

ｔ：厚さ　　　　　10[mm]

ν：ポアソン比　　0.3

　　節点座標：P₁=(0,2)、P₄=(1,2)、P₇=(2,2)、

　　　　　　　P₂=(0,1)、P₅=(1,1)、P₈=(2,1)、

　　　　　　　P₃=(0,0)、P₆=(1,0)、P₉=(2,0)

前項の計算と同じように要素1、2、3、4の変位関数の一部である[C₁]、[C₂]、[C₃]、[C₄]を計算してみます。これ以降の計算はしつこいような表示となりますが、検算用兼忘備録として示させて頂きます。尚わずか4要素でも行列は27×27行になるため、Scilabで簡単なロジックを組んで計算しました。

[C₁]=

[C₂]=

[C₃]=

[C₄]=

・・・(37)

各[C_i]の中を見ると同じような数字が並んではいますが、行列としては別物となっています。

　続いて(21)式に対応する各要素の∫[Q]^T[D][Q]dxdyを計算します。注意点は各要素で積分範囲が変わる点です。こちらもSilabで計算した結果を示します。

要素1：

∫[Q]^T[D][Q]dxdy=D₁*

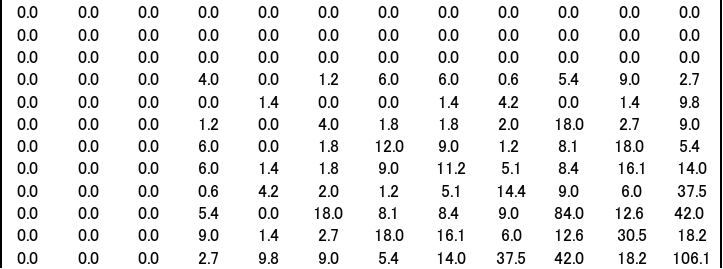
要素2：

∫[Q]^T[D][Q]dxdy=D₁*

要素3：

∫[Q]^T[D][Q]dxdy=D₁*

要素4：

∫[Q]^T[D][Q]dxdy=D₁*

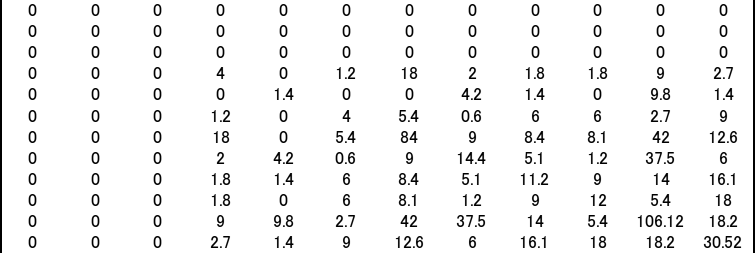
・・(38)

最後に∫[Q]^T[D][Q]dxdyを[C]^-Tと[C]^-1で挟んで剛性行列[K]を求めます。

[K₁]=D₁*

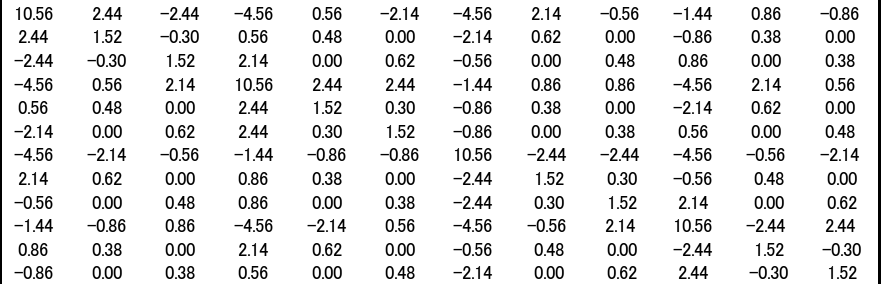
[K₂]=D₁*

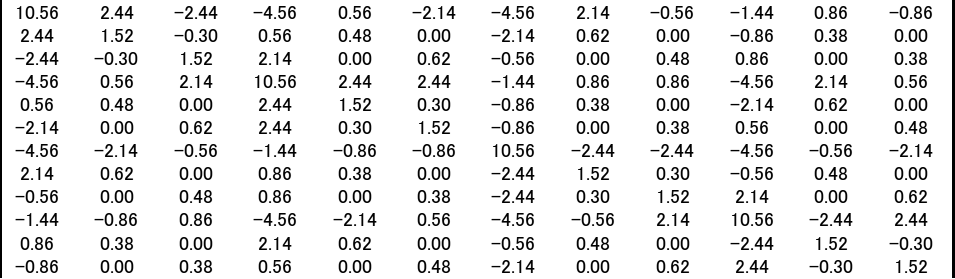
[K₃]=D₁*

[K₄]=D₁*

・・・(39)

結果は驚くことに[K₁]、[K₂]、[K₃]、[K₄]の全てが一致しています(小数点を下げていくと計算上の桁落ちによると思われる誤差は発生しています)。しかしこれは設定した節点が対称性を持っているため、当然の結果とも考えられます。逆に考えますと対称性を保った要素が集合したモデルの場合、剛性行列はそのうち1つの要素を計算すれば良いことになると考えられます。

　続いて質量行列[M]を各要素別に計算します。上述の通り、対称性が保たれているので1つだけ計算すれば良いのですが、念のため個々の要素の積分範囲で計算してみました。

　結果は予想通りすべて同じものとなりました。

[M₁]=ρt*

[M₂]=ρt*

[M₃]=ρt*

[M₄]=ρt*

・・・(40)

以上により各要素の剛性行列[K_i]と質量行列[M_i]が求められました。

次のステップとしては1次元梁の時と同様に[K_i]、[M_i]の各要素で節点の重なっている部分を足し合わせていきます。この作業が各要素間の結合を意味します。別の言い方として各要素の[K_i]、[M_i]が同時に成り立つ{δ}を探す作業となります。

　足し合わせの様子を以下に示します。P1は{δ₁}={ω、ω_x1、ω_y1}を示しており、K1は上述[K₁]を示しています。この足し合わせてにより４要素の結合がなされます。

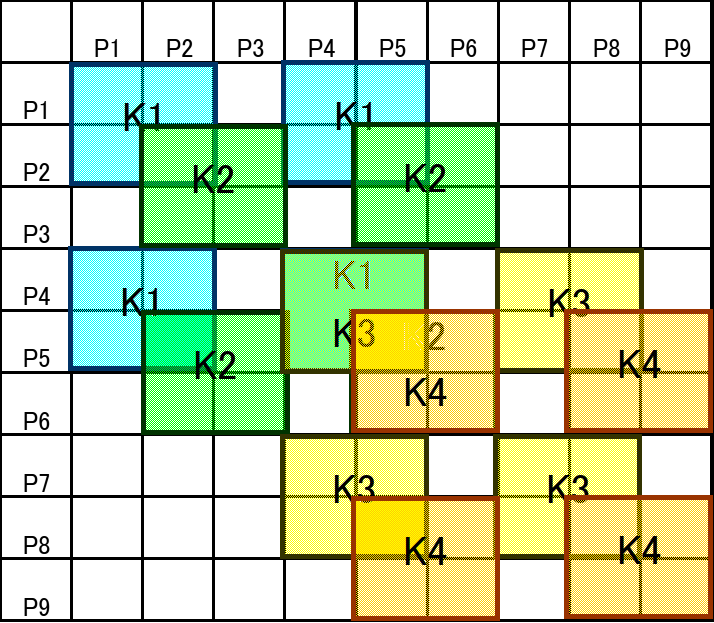
非常に小さくて恐縮ですが、Scilabを用いて計算した全体の剛性行列[K]を示します。

[K]=D₁*

・・・(41)

同様に質量行列[M]も計算します。

[M]=ρt*

・・・(42)

拘束点を点{1,2,3,4,6,7,8,9}とします。そうすると境界条件として以下となります。

{δ₁、δ₂、δ₃、δ₄、δ₆、δ₇、δ₈、δ₉} = {0}　・・・(43)

この境界条件により[K](41)、[M](42)のP5の行、P5の列以外は計算する必要がなくなります。

この点を反映した剛性行列と質量行列を[Kf]、[Mf]とすると(41)(42)式中に薄色で着色したところだけ残ることとなります。

[Kf]=D₁*

・・・(44)

[Mf]=D₁*

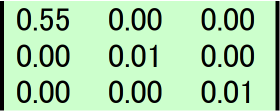
・・・(45)

SciabのコマンドKM=[M]^-1[K]、[P,D]=spec(KM)を用いて計算した結果を以下に示します。

[P]=

・・・(46)

[D]=

・・・(47)

f =

・・・(48)

[P]の第１列のうち、ω(Z方向変位)を3次元plotしてみます。これが1次モードの形となります。

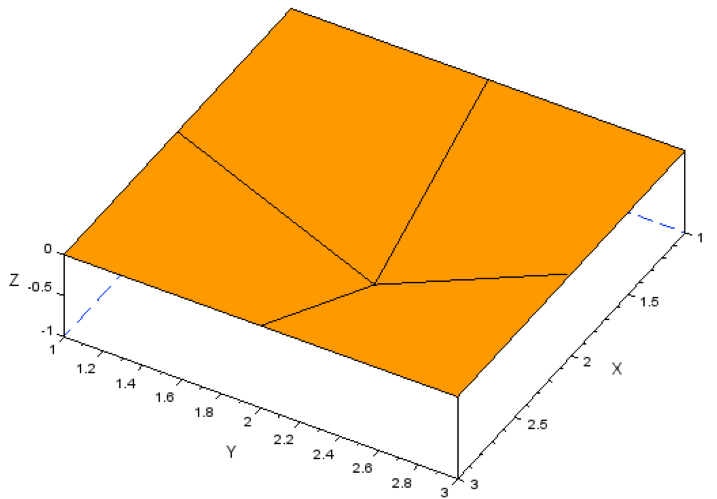
(48)式の確からしさを梁の理論式より確認します。

全周固定薄板の固有振動数に関する理論式（参考文献[2]）

・・・(49)

固定-自由端　λ₁²=35.99、λ₂²⁼73.41、λ₃²=108.3

∴ f₁=21.67Hz、f₂=44.20Hz、f₃=65.20Hz・・・(50)

(48)式の最小振動数f=21.14Hzは上記1次モードと十分一致しており、有限要素による解法の妥当性が示せたと考えます(4要素では2次モード以降は一致しないようです）。

２．３　10ｘ10要素板の計算

　もう少し要素を増やした計算を実施してみます。500x500x0.5mmのアルミ薄板の周辺を固定した場合の固有振動数をScilabを用いて計算して見ました。結果をモード次数5までを以下に示します。FEMとしては粗い10ｘ10マスでも理論値との十分な一致を示しています。

E：ヤング率　　　7e10[Pa]

ρ：密度　　2800[kg/m3]　　　　　　　　

Ｌ：要素の縦長さ 50[mm](10ｘ10マスで500ｘ500ｍm)　　　　　・・・(51)

ｔ：厚さ　　　　　0.5[mm]

ν：ポアソン比　　0.3

計算結果

1次モード：固有振動数　17.16Hz（理論値　17.33Hz）

２次モード：固有振動数　34.91Hz（理論値　35.36Hz）

3次モード：固有振動数　50.64Hz（理論値　52.16Hz）

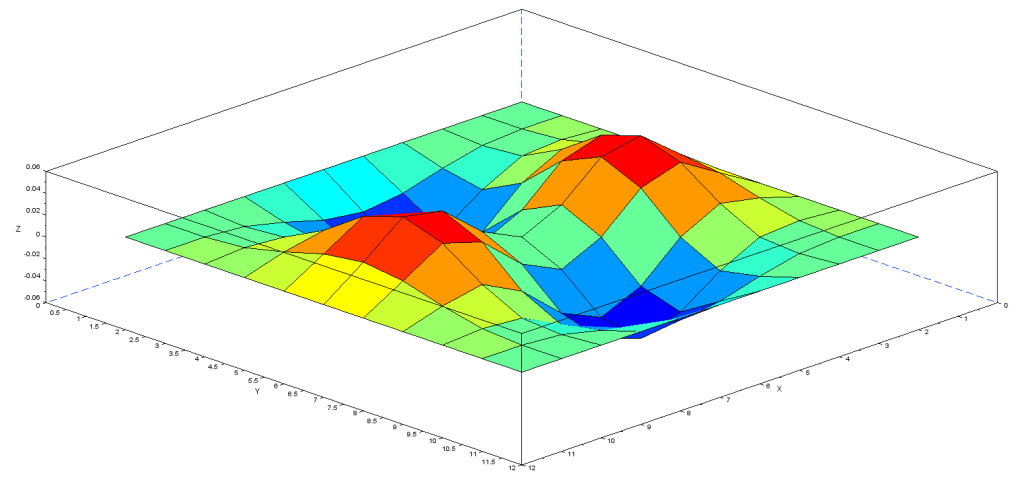
4次モード：固有振動数　62.62Hz（理論値　63.38Hz）

5次モード(ｚ方向反転図)：固有振動数　63.00Hz（理論値　63.67Hz）

　１次モードでは凸部が一つ、２次モードでは凸部が２つ、３-４次モードでは凹凸部が４つと規則正しく増加していく様子が見て取れます。この解析結果では見ずらいですが５次モードでは5つの凹凸部が形成されます。正方形において対称性を維持しながら凹凸部が増えていくようです。

　尚併記した理論計算値は以下の式から計算しました。式は参考文献[2]に拠ります。

　　固有振動数計算理論式

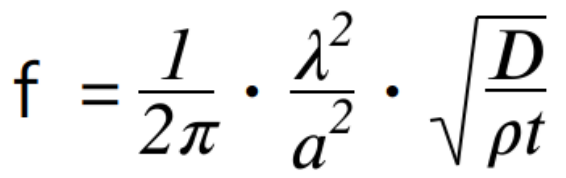
・・・(52)

λ²=35.99(1次)、73.41(2次)、108.3(3次)、131.6(4次)、132.2(5次)

　a：板の1辺の長さ[0.5m]

　Ｄ：曲げ剛性(式(2)と同じ) [E=7*10^10Pa][ν=0.3](Scilabの計算でもこの値を使用)

　ρ：密度[2800kg/m3](Scilabの計算でもこの値を使用)

　t：板厚[0.0005m]　補足となりますが10ｘ10マスを更に増やしていくと更に緻密な描写が得られますが、これ以上マスを細かくしていくとPCの性能上メモリーオーバーでハングしてしまいます。当面、当事業所での解析はこのレベルが限界となります。

　以上の計算で固有振動数及びその時の形状を解析で得てきました。実際の現場では更に動的な変化が重要となります。そこでこちら(Deail2)にて動的挙動解析を検討してみます。

参考文献

[１]機械構造振動学 MATALBによる有限要素法と応答解析　小松敬冶著　森北出版株式会社

[２]機械振動学　岩田佳雄・佐伯暢人・小松崎俊彦共著　数理工学社