以下の写真は私のバイクのマフラー周りを撮影したものです。アンダーシート・マフラーとなっておりデザインがとても気に入っています。一方設計する側に立つとマフラー周りの温度管理は厳しいものだったと想像します。エンジン直後のエキゾーストではタバコの火がつくくらいの高温です。もちろんマフラーまでくれば、そこまでは高温ではないのですが、それでも写真の通り、マフラー周りには多くのプラスチック部品が存在します。

　このあたりの熱環境をOpenFoamにて解析してみようと思います。

　尚このアンダーシート・マフラーは見た目が一番の長所ですが、以下の点も長所となります。

・立ちごけ、衝撃の少ない転倒ならばマフラーに荷重がかかりません。

　マフラーに大きな荷重がかかるとエキゾースト付け根からのガス漏れが酷くなる傾向があると思います。

---

１．１　モデル設定

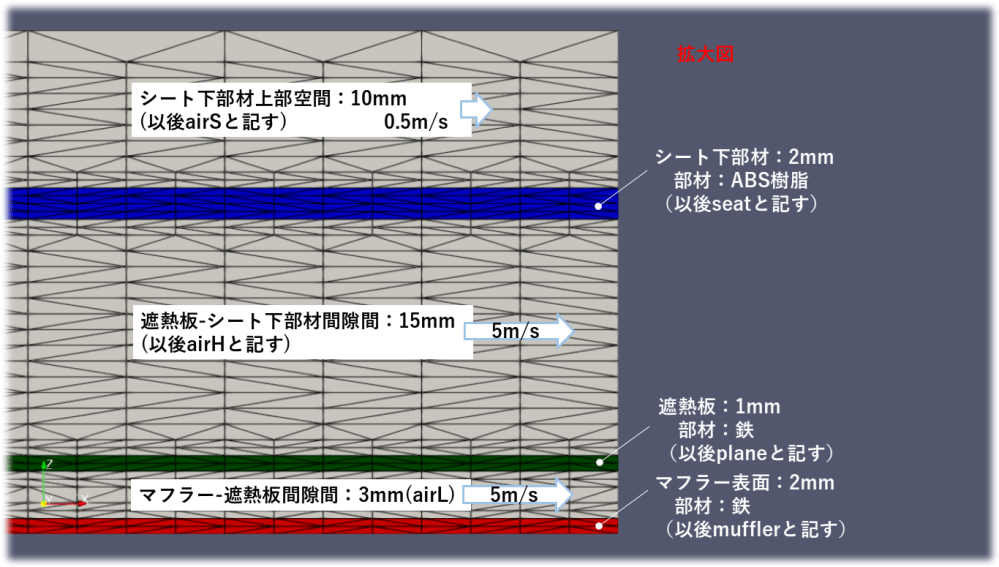
モデルのメッシュの様子を以下に示します。

・メッシュ：250(長さ) x 32(高さ) x90(幅)[mm]を10x8x9の合計720マスに分割。

　その後ほぼ全域を2²分割。更にマフラー、遮熱板、シートの表面を2¹分割。

・マフラー(鉄:2[mm])と遮熱板(鉄:1[mm])の隙間が3[mm]。冷却風を5[m/s]と設定。

・遮熱板(鉄:1[mm])とシート下部材(ABS樹脂:2[mm])の隙間が15[mm]。

　冷却風を5[m/s]と設定。

・シート下部材(ABS樹脂:2[mm])の上方空間は10[mm]。冷却風を0.5[m/s]と設定。

・結果、出来上がったメッシュが以下の図となります(最小厚み0.5[ｍｍ])。

---

１．２　OpenFoam設定

Openfoamの設定を以下に示します。

[材料特性]

・マフラー材料特性：鉄として以下を設定

　熱伝導率：80[W/m/K]

　比熱：450[J/kg/K]

　密度：800[kg/m³](実際の1/10に設定：温度収束時間を1/10にするため)

　放射率：1(実際は0.8程度のようだが、今回は検算を単純にするため「１」とした)

・遮熱板：鉄としてすべてマフラーと同一とした

・シート下部材：ABS樹脂として以下を設定

　熱伝導率：0.2[W/m/K]

　比熱：1500[J/kg/K]

　密度：105[kg/m³](実際の1/10に設定：温度収束時間を1/10にするため)

　放射率：1(実際は塗装と同様な0.9位と推定するが、マフラーと同じ理由で「1」とした)

　　　　　尚シート部材の上の空間については空気熱伝達のみとし、輻射は含めない設定とした。

[初期温度]

・マフラーは500[K](230℃)とした(適当：相当熱い設定)

・その他はすべて300[K](30℃)とした

[速度]

・airL(図中定義)及びairHを5[m/s](適当：この程度は実現出来ると想定)とした

・シート下の流れはほとんどないと考え、airSは0.5[m/s](適当)とした

[圧力]

・圧力：全域初期値1e+5[Pa]に設定。

[ソルバー定義]

　以下を除きOpenFoam輻射解析の機能確認における設定と同じ設定とした。

・乱流エネルギーk、乱流散逸率epsilonの初期値設定は以下。設定根拠はこちらを参照方。

　　airL：[k=3.75e-3、epsilon=1.8e-1]

　　airH：[k=3.75e-3、epsilon=3.6e-2]

　　airS：[k=3.75e-5、epsilon=5.4e-5]

・積分幅：初期0.00005sec、クーラン数0.7で可変

[補足]

・通常入口側で速度を定義しますが、狭い空間に空気を一定速度で入れ込もうとしたため結構な脈動が発生してしまいました。そこで今回は出口で速度を固定しました。

それでも狭い空間の流れは均一にはならず、中央速度が周囲速度より2倍近く増速してしまいました。

・幅方向は実際は200[mm]程度ありますが、90[mm]に縮小しました。他計算例で示しました疑似2Dを目安に境界条件を設定しています。具体的には両サイドの境界条件はzeroGradientと設定しました。

・疑似2Dなのに90[mm]もの幅を持たせたおかげで、輻射熱の収支がよく一致しています(薄いと収支が合いません)。

---

１．３　計算結果

　120秒後の計算結果を示します。

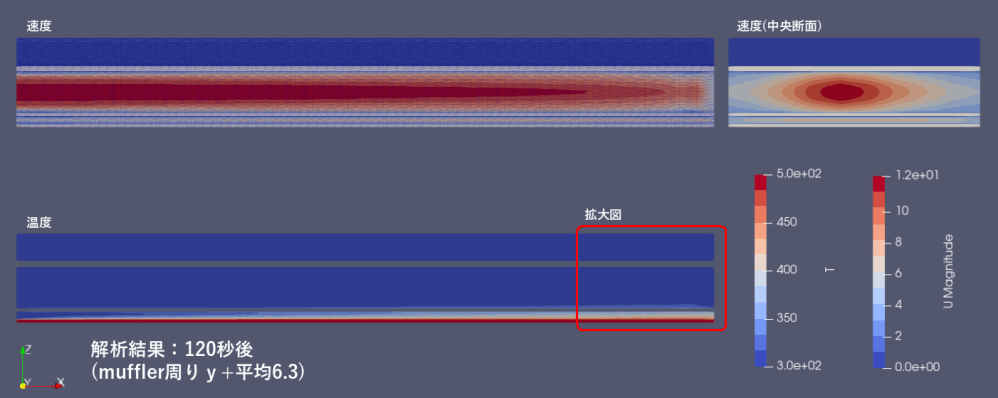
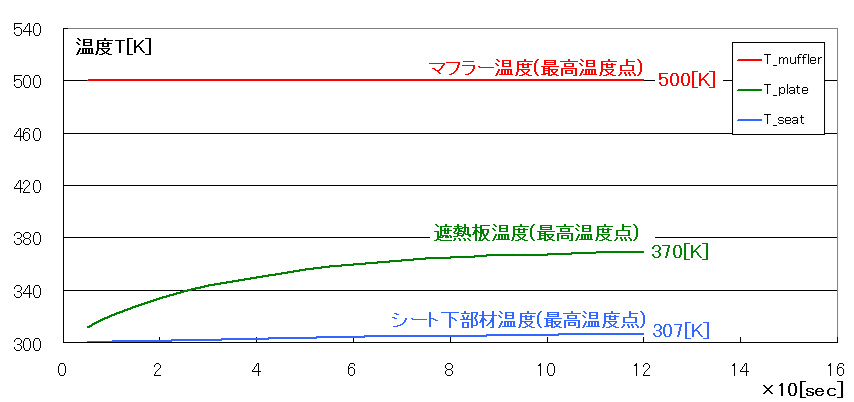
　結果、次のことが分かりました。

・遮熱板は70[K]まで昇温していますが、シート下部材の温度は僅か7[K]に収束しそうです。

（自分のバイクの経験上はもう少し温度が上がっているように感じます。これについては後述します(1.4.2(1)項）。

・輻射熱は温度の４乗で効きますのでマフラー500[K]と遮熱板370[K]では周囲温度300[K]に対し20%=(370⁴-300⁴)/(500⁴-300⁴)まで輻射熱が軽減されます。

・遮熱板とシート下部材の間の風の流れは遮熱板だけでなく、シート下部材も良く冷却しています。　これらの検算を次項に示します。

---

１．４　計算結果の確認

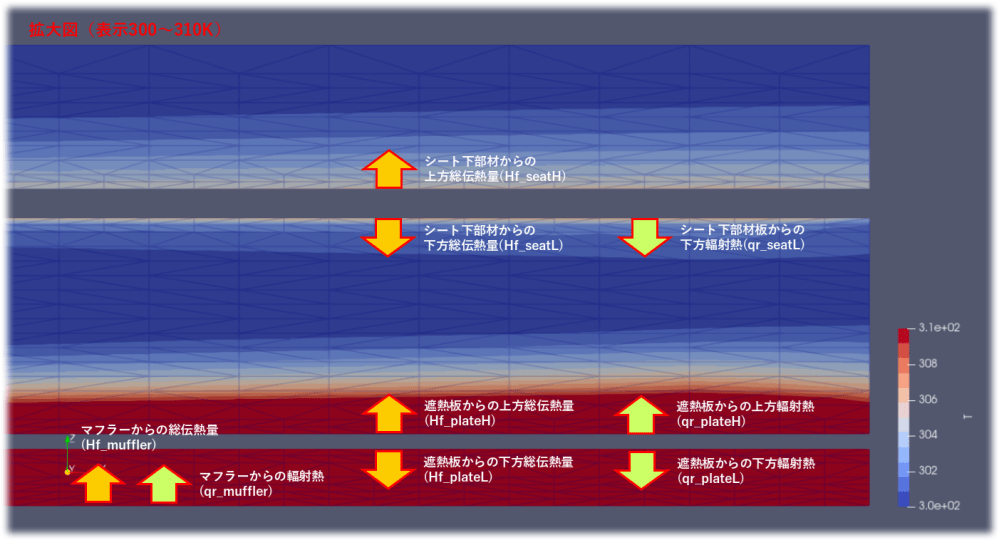
１．４．１　輻射熱の様子

（１）マフラー-遮熱板間

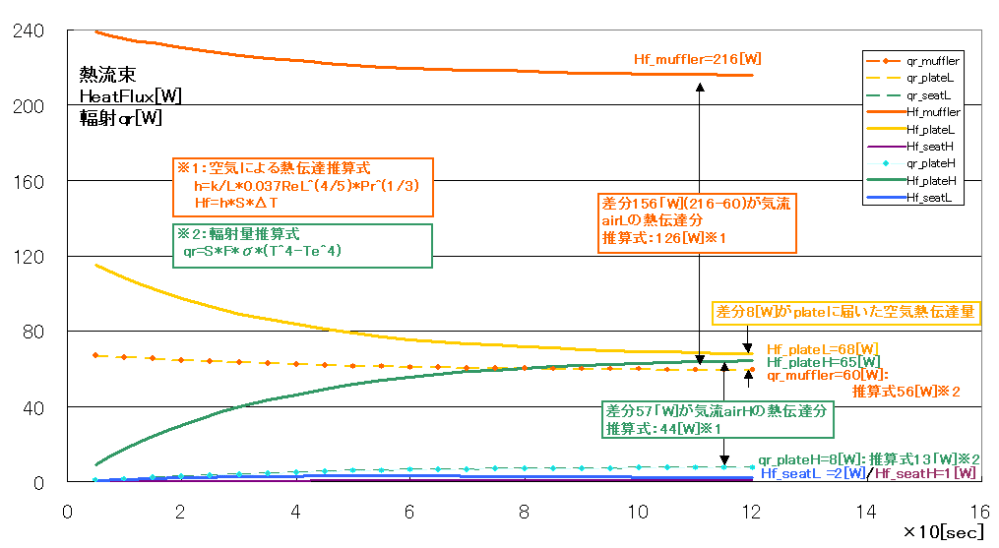
　マフラーからは60[W](qr_muffler)、遮熱板も60[W](qr_palteL)と収支が一致しています。

　この値は以下の推算式結果56[W]と良く一致しています。

　　　　形態係数を用いた物体からの輻射熱推算式

　　　 qr=F×S×σ×(T_m⁴-T_p⁴)=55.8[W]

（２）遮熱板-シート下部材間

　遮熱板からは8[W](qr_plateH)、シート部材も8[W](qr_seatL)と収支が一致しています。

　この値は以下の推算式結果13[W]とだいたい一致しています(関連文章[1]4.4.3項)。

 （この差は輻射面に温度むらがあるのに最高温度を使用しているためと考えられます）

　　　 qr=F×S×σ×(T_m⁴-T_p⁴)=12.6[W]

１．４．２　すきま風による熱伝達の様子

（１）マフラーからの放出熱量

　マフラーからの総熱量は216[W](Hf_muffler)で、このうち60[W]が輻射熱によるものなので空気熱伝達量は156[W]となります。この値は以下の推算式(関連文章[1]3.6.2項)の結果126[W]とだいたい一致しています(それでもそれなりの差なので「追記２」で再確認します)。

　　　　平板の乱流強制対流による熱伝達量推算式

　　　　h=k/L×0.037R_eL^4/5*Pr^1/3=28.1[W/m2/K]

　　　　R_eL=U×L /ν=69444

　　　　Hf=h×S×ΔT=126[W]

　　　　　k：空気の熱伝導率　0.0286[W/m/K]

　　　　　L：平板全長　0.25[m]

　　　　　U：風速　5[m/s]

　　　　　ν：空気の動粘度　1.8e-5[m²/s]

　　　　　Pr：空気のプラントル数　0.7

　　　　　S：冷却面積　0.09×0.25[m²]

　　　　　ΔT：冷却風との温度差　200[K]

　尚本CFD計算は乱流を想定してソルバーにRASを用いましたが、壁関数ｙ+≒6.3の状況から層流と推定されます。この場合推算式は以下(関連文章[1]3.4.1項)になり上述乱流の式よりも冷えない状況となります。実際経験上シート下温度上昇が7[K]よりも大きく感じるのはこの点からかもしれません。

　　　　平板の層流強制対流による熱伝達量推算式

　　　　h=k/L×0.664R_eL^1/2*Pr^1/3=17.8[W/m²/K]

　　　　ReL=U×L /ν=69444

　　　　Hf=h×S×ΔT=80[W]

（２）遮熱板の空気熱伝達による吸収量

　遮熱板の吸収した総熱量は68[W](Hf_palteL)で、このうち60[W]が輻射熱によるものなので空気熱伝達量はわずか8[W]となります。5[m/s]＆3[mm]の隙間風のおかげでマフラーから放出された空気伝達量156[W]のうち、遮熱板にたどり着くのは僅か8[W]で、そのほとんどを防ぐことが出来ています。

（３）遮熱板から上方への放出熱量

　遮熱板からの総熱量は65[W](Hf_plateH)で、このうち8[W](qr_plateH)が輻射熱によるものなので空気熱伝達量は57[W]となります。この値は以下の推算式結果44[W]とだいたい一致しています(関連文章[1]3.6.2項)。

　　　　平板の乱流強制対流による熱伝達量推算式

　　　　h=k/L×0.037R_eL^4/5*Pr^1/3=28.1[W/m²/K]

　　　　ReL=U×L /ν=69444

　　　　Hf=h×S×ΔT=44[W]

　　　　ΔT：冷却風との温度差 70[K](=370-300)

　また温度領域(310[K]が3[mm]位)は以下の概算から伺えます。

　　　半無限固体の熱伝導方程式の解

　　　熱源が温度定義の場合(関連文章[1]2.3.3項)

　　　ΔT=(Th-Te)[1-erf(x/(2√(αt)))]

　　　α=k/(ρC)=2.33e-5

　　　ｋ：熱伝導率　空気 0.0286[W/m/K]

　　　ρ：密度　空気 1.225[kg/m³]を使用

　　　Ｃ：定圧比熱　空気1000[J/(kg・K)]

　　　erf(ξ)=２/√π・∫e^-y2dy|_y=0～ξ：誤差関数(エクセルの関数に含まれています)

　上式に以下を代入してみます。

　　　x=2[mm]：310[K]が3[mm]位から境界層分として1[mm](適当)を引きます。

      t=0.25/5=0.05[sec]：すきま風滞在時間

　　∴ΔT=70*[1-erf(0.002/2√(0.05α))]=13[K]　＜＝OpenFoam結果310[K]と十分一致。

１．４．３　輻射による昇温の様子

（１）シート下部材の昇温

　シート下部材の下方からの総熱量(吸熱)は2[W](Hf_seatL)で、このうち8[W](qr_seatL)が輻射熱によるものなので空気熱伝達量(放熱)は6[W]となります。

　注意すべきは樹脂のような熱伝導率が低い物質の場合、表面を輻射で炙られると熱が内部に拡散するまで表面温度が高くなる点と考えます。

　この点を以下の推算式で確認しておきます。

　　　半無限固体の熱伝導方程式の解

　　　熱源が熱量定義の場合(関連文章[1]2.3.3項)

　　　ΔT=2qs/k×√(αt/π)=17[K]or4[K]

　　　α=k/(ρC)=2.33e-5

　　　ｋ：熱伝導率　空気 0.0286[W/m/K]

　　　ρ：密度　空気 1.225[kg/m³]を使用

　　　Ｃ：定圧比熱　空気1000[J/(kg・K)]

　　　qs：輻射熱 8[W]or2[W]

　　　ｔ：経過時間　今回は120秒

　結果、入力を8[W]にした場合17[K]の昇温、入力2[W]にした場合4[K]の昇温となりOpenFoamの計算結果である7[K]と平均値がおおよそ一致しています。　但し上述の通り、熱伝導率の低い物質では表面が高温になる点を注意する必要があると思います。

---

「追記１」

　本文にてマフラー周りの熱の様子が分かりました。ここでは遮熱板がない場合はどうなるかを計算してみます。

　本文のモデルから遮熱板だけを無くした場合を計算します(epsilon初期値のみ0.0284に変更)。

結果が以下となります。

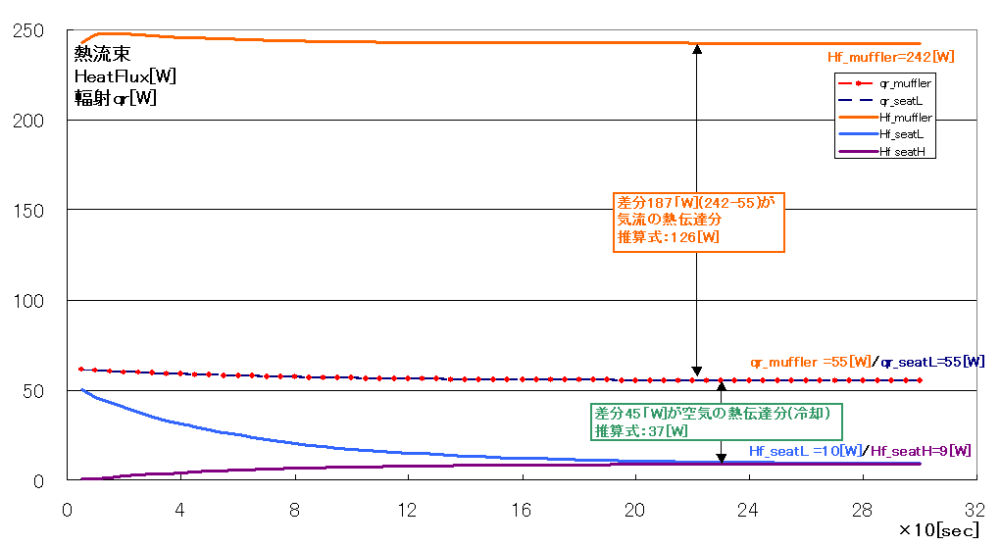
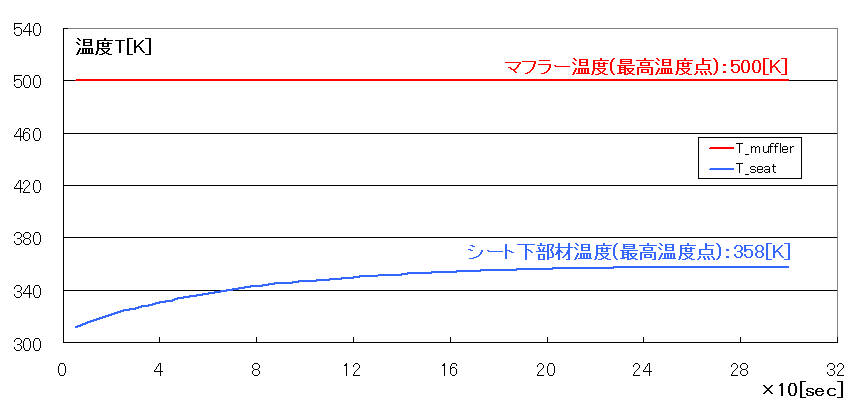
　シート下部材温度が358[K](88℃)に上昇してしまいました。シート下には電気装備品がいくつかありますし、ユーザーも触る場所です。またABS樹脂の熱変形温度は70～90℃程度だそうなので、遮熱板が必要と感じます。(但し解析の出発点であるマフラー温度500[K](230℃)は私の適当な仮定です)。

　本文と追記１の計算結果から遮熱板設計の肝は以下だと感じました。

・発熱体が平面の場合、輻射熱は距離を離しても減らない。(60[W]⇒55[W])

・遮熱板を途中に挟むことでマフラーからの膨大な熱量を輻射熱だけに絞る。

・遮熱板を外気で冷やすことでマフラー本体よりも相当な温度低下が見込める。(500[K]⇒370[K])

・結果、目的物(シート下部材)への輻射熱を大幅に減じることが出来る。(60[W]⇒8[W])vs(Δ58℃⇒Δ7℃)

　なお遮熱板とシート下部材の冷却流量の確保がこの仕組みの重要な点ということも書いておきたいです。本文の計算でもなかなかスムーズに流れてくれませんでした。実際もかなり注意が必要な設計領域と感じます。

---

「追記２」

　マフラーからの空気熱伝達量に関しopenfoam計算値156[W]と推算値126[W]にそれなりの差が出ています。「追記１」の計算ではopenfoam計算値187[W]に対し推算値126[W]と更に差が大きくなってしまっています。

　この原因として以下の２つを考えています。

①風速

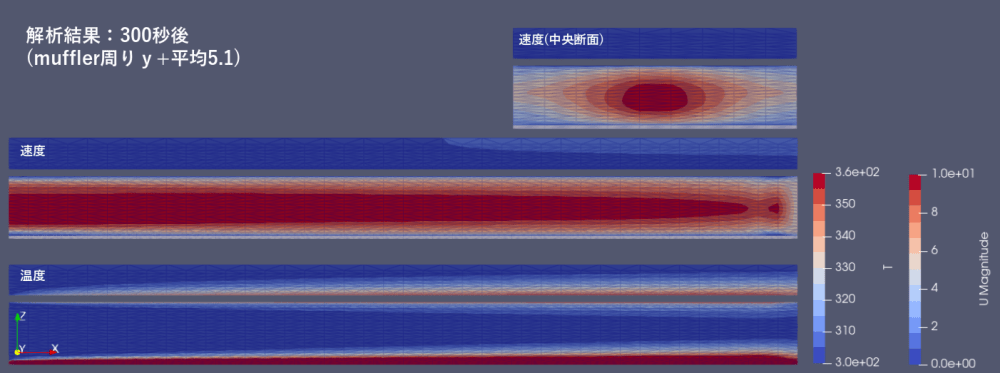
　推算式では速度5[m/s]の一様流として計算していますが、openfoam計算では下図のごとく速度にむらが出ています。本文では中央で12[m/s]、追記では10[m/s]に達しています。

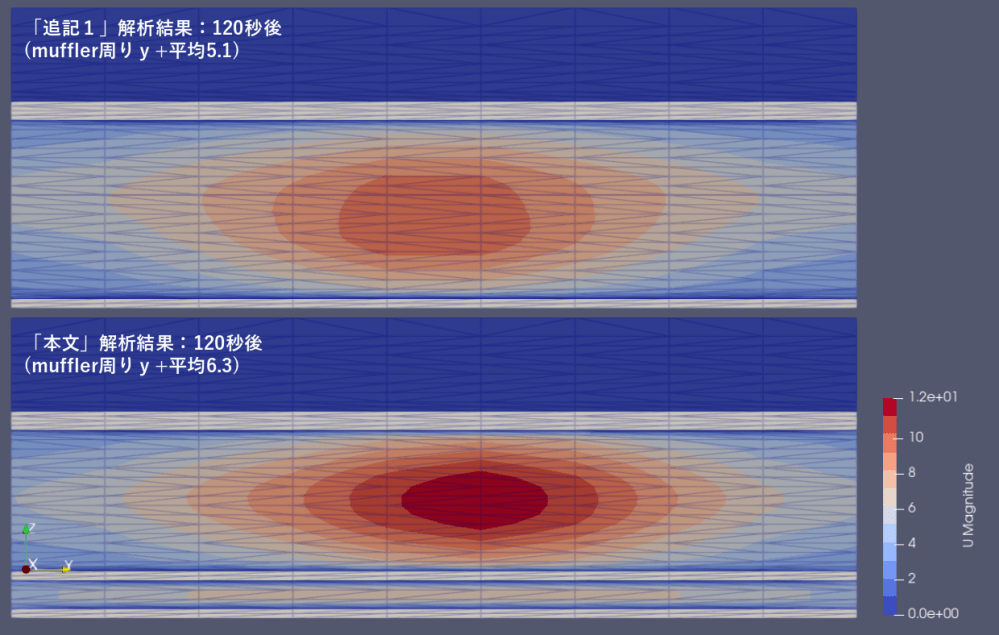
②乱流計算(RAS)

　壁関数ｙ+の様子(平均6.3)から冷却風が遅すぎます。

　単純なモデルでこれらを改善した計算を実施して見ます。

結果が以下でかなりな一致を見ることが出来ました。

　マフラーからの空気による熱伝達量

　OpenFoam計算値：223[W]

　推算値　　　　　：237[W]

　実は本計算で風速10[m/s]としましたが、これを20[m/s]に上げますと今度はOpenFoam計算値290[W]に対し推算値は383[W]で推算値の方がかなり大きくなってしまいます。未確認ですが風速20[m/s]時の熱伝達の主役となる対流(渦)に対し、メッシュが粗すぎるため十分な熱伝搬が表現出来ていないと推定します。

　OpenFoam計算値と推算値が全速度域で一致するのは難しいと感じました。この意味からも一般的に言われているCFDと試験値のCalibration/Correlationの重要性を感じます。

　この簡易モデルの変更点は以下です。

・シート下部材も省略し、マフラーと冷却風のみの解析空間

・風速(U)

　入口速度10[m/s]で固定。出口はzeroGradient。壁面、天井はslip。

　(風速10[m/s]でもまだ壁関数ｙ+は十分な大きさになっていません)

・圧力(p_rgh)

　出口を1e5[Pa]で固定。その他はすべてzeroGradient。

・k初期値は0.00375、epsilon初期値は0.0284は「追記１」から不変。

・radiationPropertiesファイルにて「radiation off」

---