バネ-マス系の自励振動
「テーマ」
・Scilabを用いてバネ-マス系の自励振動を解析する
「方針」
一般的にバネ-マス系の振動は周期的外力によって引き起こされます。その外力の周期と系統の固有振動数が一致すると共振現象となります。ところが系統を安定方向にもっていくはずの摩擦が原因でバネ-マス系が自励振動を起すことがあります。
ここではその現象をScilabを用いて解析してみます。
1.解析設定
検討対象は適当に以下の状況としました。
・ベルトコンベア上に質量m=1[㎏]の荷物
・荷物はバネ定数k=1000[N/m]のバネで固定
・コンベア移動速度はVb=2[m/s]
運動の様子を推定すると荷物が一定距離ずれたところでバネ力とベルトコンベアの滑り抵抗が静的に釣り合う状態となりますが、動摩擦が静止摩擦よりも小さい場合、自励振動が発生します。

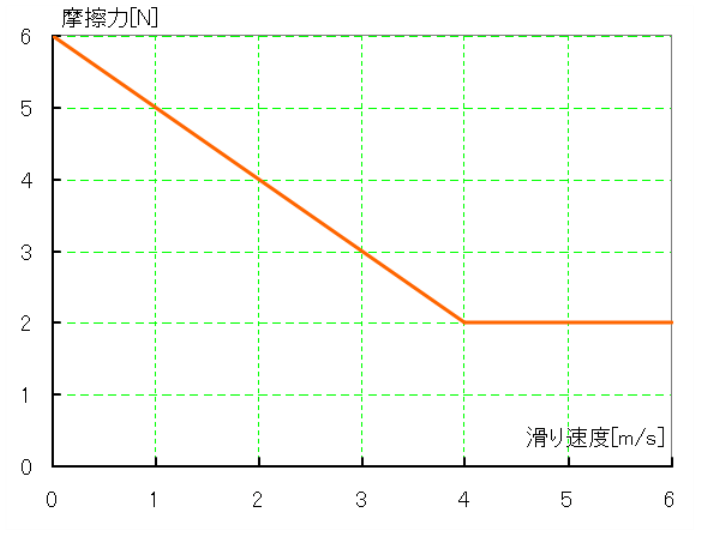
摩擦力として以下の状況を想定します。
摩擦力(絶対値):|F(Vrel)[N]|=6 – Vrel[m/s] (0[m/s] < Vrel < 4[m/s])
:|F(Vrel)[N]|=2 (4[m/s] < Vrel )
静止摩擦力が動摩擦力の3倍位に設定しましたが、現実も十分ありうる状況です。但し横軸滑り速度(Vrel)に関しては現実よりもかなり大きなものに設定しました。
運動方程式は以下となります。
m・d2x/dt2 = -k・x +F(Vrel) ・・・(1)

摩擦力F(Vrel)をベルトコンベアの速度Vb=2[m/s]での摩擦力F(Vb)=4[N]とそれ以外という式に分けると以下の式で書き直せます(参考文献[1]8章)。
F(Vrel)=F(Vb)+(Vb-Vrel)
=F(Vb)+V ・・・(2)
V:固定座業系での速度(=dx/dt)
Vrel:ベルトと荷物の間の相対速度
Vb:ベルトの速度2[m/s]
Vrel = Vb-V
(1)に(2)を代入し、F(Vb)=4[N]と釣り合うばね力k・δの位置を中間位置にすると以下に書き換えられます。
m・d2x/dt2 = -k・x +V <= Vは発散力として存在します。
∴ m・d2x/dt2 -dx/dt +k・x =0 ・・・(3)
x(t)=eλtと置くと特性方程式は以下となります。
mλ2 – λ + k = 0 ・・・(4)
(4)式を解くことにより一般解が求められ、運動が解析的に求められます(手計算出来ます)。
2.Scilab
以下にベルトコンベア上の荷物の運動を解析するためののモデルを示します。
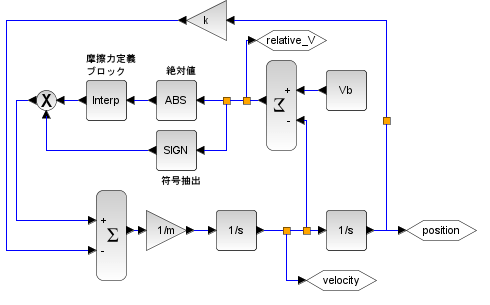
・パタメータ
m:質量 1[kg]
k:ばね定数1000[N/m]
Vb:ベルトコンベア速度 2[m/s]
摩擦力定義ブロック:既述の形状で定義
<position>、<velocity>、<rerative_V>:計算結果抽出点
・積分条件
積分方式:ルンゲクッタ
積分幅:5msec
3.解析結果と考察
解析結果をグラフに示します。

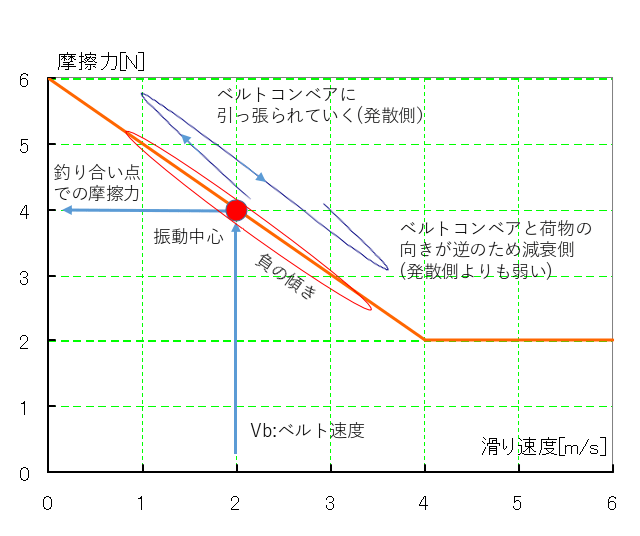
計算開始直後から自励振動が始まっています。それぞれの様子を詳しく見てみます。
・自励振動の増加率:(4)式よりλ(実数部)=1/2[m]で指数関数的増加(時定数τ=1/λ=2[sec])。
・中立位置:摩擦係数の中間位置でバランス。kδ=F(Vb) ∴δ=4/1000=4[mm]
・相対速度(rerativ_V):解析開始時にVb=2[m/s]で開始し、0[m/s]まではベルトコンベアに引っ張られ続けます。バネの反動で反対方向には同程度まで振れます。この間0[m/s] < Vrel < 2[m/s]の区間では発散力、2[m/s] < Vrel < 4[m/s]の区間では減衰力として働きます。発散力の方が強いため(摩擦力定義曲線が左上がり)どんどん増幅していく状況となります。
・固定座標系速度(velocity):Vbから相対速度を引いた-2[m/s] < V < 2[m/s]の区間で振動します。
・収束区間:固定座標系速度の片幅2[m/s]に対応した範囲V/ω=2/√1000=66[mm]の幅の近傍で振動しています。
以上を物理現象的に説明してみようと思います。
・ベルトコンベアからの摩擦力エネルギーの源泉であるベルトコンベア速度2m/sが打ち消されるまでは振幅が増大していきます。
・その間バネ系の固有振動数で振動し続けながら成長していきます。
・ベルトコンベアの速度を超えると摩擦力の向きは減衰力の向きに代わるため、そこで発散が収束を迎えることとなります。
(この現象は参考文献[1]8章にて負性抵抗による自励振動として説明されています。)
参考に摩擦力のパターンを変えた場合の計算結果を示しておきます。
〇パターン1:
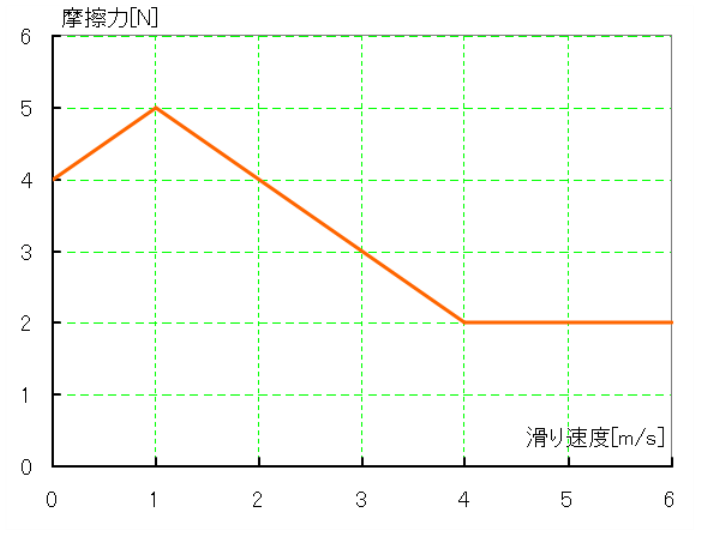

0[m/s]付近の摩擦力が小さくなった分、ピークまでに達する時間が若干長くなっていますが、前の計算結果とほとんど変わりませんでした。
〇パターン2:


釣り合い点前後の摩擦力が対称のため、発散していません。
参考文献
[1]航空宇宙工学テキストシリーズ 空力弾性学 中道二郎 玉山雅人 児玉智 共著 丸善出版
